题目描述

解题思路

贪心

🔗

DP

• 确定dp数组（dp table）以及下标的含义

dp[i]：包括下标i之前的最大连续子序列和为dp[i]。

• 递推公式

dp[i]只有两个方向可以推出来：

• dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
• nums[i]，即：从头开始计算当前连续子序列和

一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

• 初始化

dp[0]是递推公式的开始，所以初始化为nums[0]。

• 遍历顺序

有递推公式可以知道从前先后遍历。

• 打印dp数组

以示例一为例，输入：nums = [-2,1,-3,4,-1,2,1,-5,4]，对应的dp状态如下：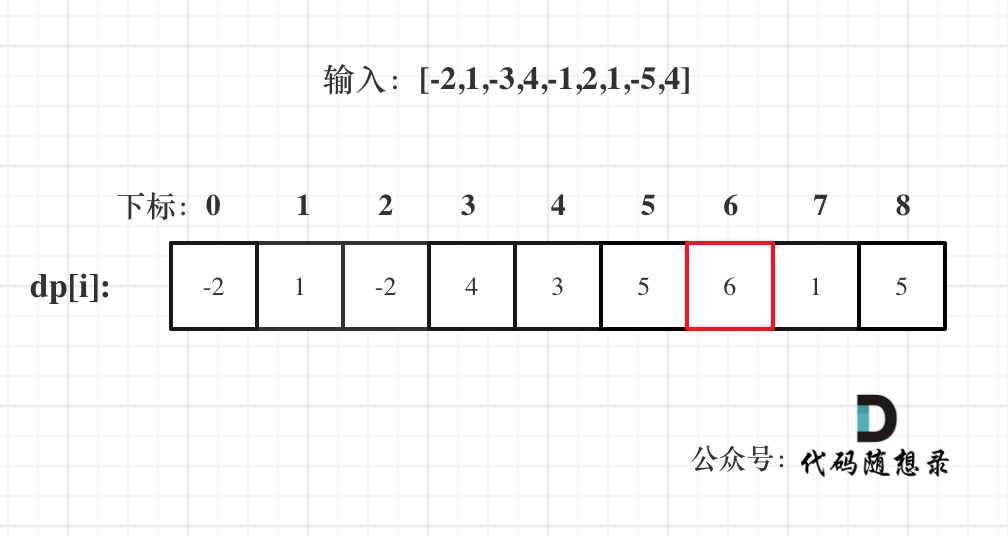
注意最后的结果可不是dp[nums.size() - 1]！ ，而是dp[6]。
在回顾一下dp[i]的定义：包括下标i之前的最大连续子序列和为dp[i]。
那么我们要找最大的连续子序列，就应该找每一个i为终点的连续最大子序列。
所以在递推公式的时候，可以直接选出最大的dp[i]。
所以需要找出每个dp中最大的数。

/**
         * 动态规划
         *
         * @param nums
         * @return
         */
public int maxSubArray(int[] nums) {
    if (nums.length == 1) {
        return nums[0];
    }
    // dp[i]：包括下标i之前的最大连续子序列和为dp[i]
    int[] dp = new int[nums.length];
    dp[0] = nums[0];
    int result = dp[0];
    for (int i = 1; i < nums.length; i++) {
        //                dp[i]只有两个方向可以推出来：
        //                dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
        //                nums[i]，即：从头开始计算当前连续子序列和
        //                一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
        dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
        if (dp[i] > result) result = dp[i]; // 取出最大的
    }
    return result;
}

优化

// 利用动态规划的特性，直接在原数组上操作
// 空间复杂度降到O(1)
public int maxSubArray(int[] nums) {
    int res = nums[0];
    for (int i = 1; i < nums.length; i++) {
        nums[i] += Math.max(nums[i - 1], 0);
        res = Math.max(nums[i], res);
    }
    return res;
}