二叉树的概述

二叉树的性质

• 在二叉树的第i层上之多有 （2 的 i-1 次方）个节点
• 深度为k的二叉树至多有 （2 的 k 次方） - 1 个节点（k >= 1）
• 对于任何一棵二叉树 T ，如果其终端节点数为 n0 ， 度为2的节点数为 n2 ，则 n0 = n2 + 1
• 具有 n 个节点的完全二叉树的深度为 [log2 n] + 1
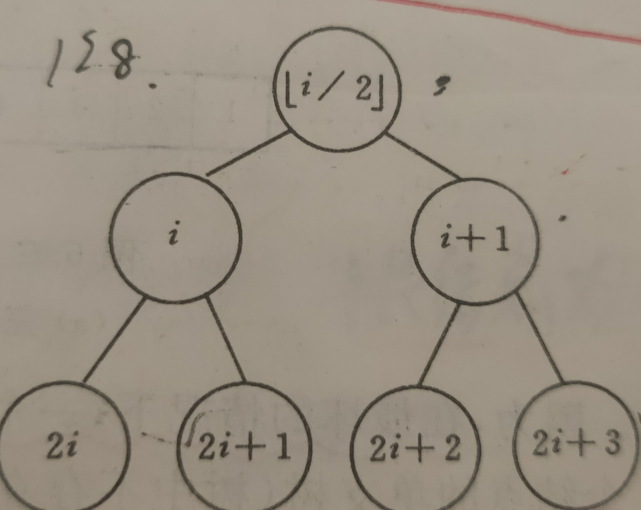
• 如果对一棵有n个节点的完全二叉树的节点按层序编号（从第1层到第[log2 n] + 1层，每层从左到右 ），则对任意一节点i（1 <= i <= n），有

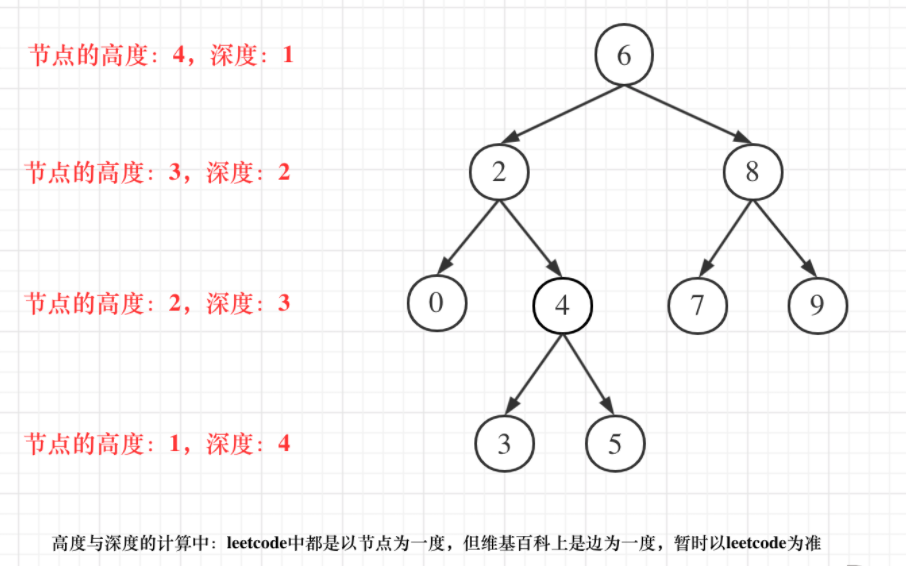
深度和高度的区别

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

对于某个节点来说：

• 深度是指从根节点到该节点的最长简单路径边的条数；
• 高度是指从最下面的叶子节点到该节点的最长简单路径边的条数；

对于二叉树来说：

• 深度是从根节点数到它的叶节点；
• 高度是从叶节点数到它的根节点；

注意： 树的深度和高度一样，但是具体到树的某个节点，其深度和高度不一样。

习题目录