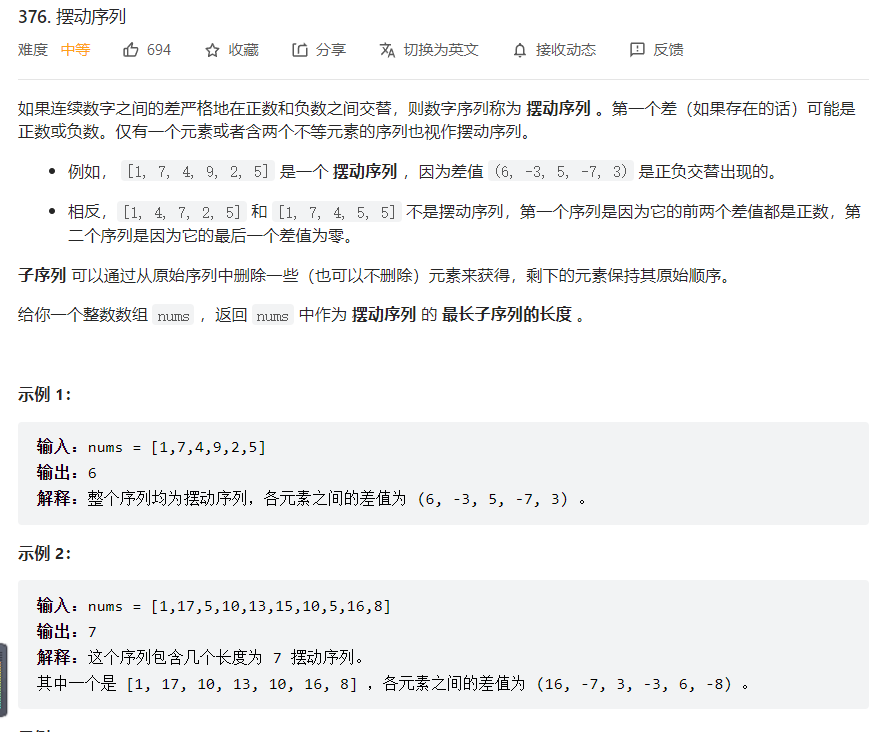
题目描述

image.png

解题思路

贪心

局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。
整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。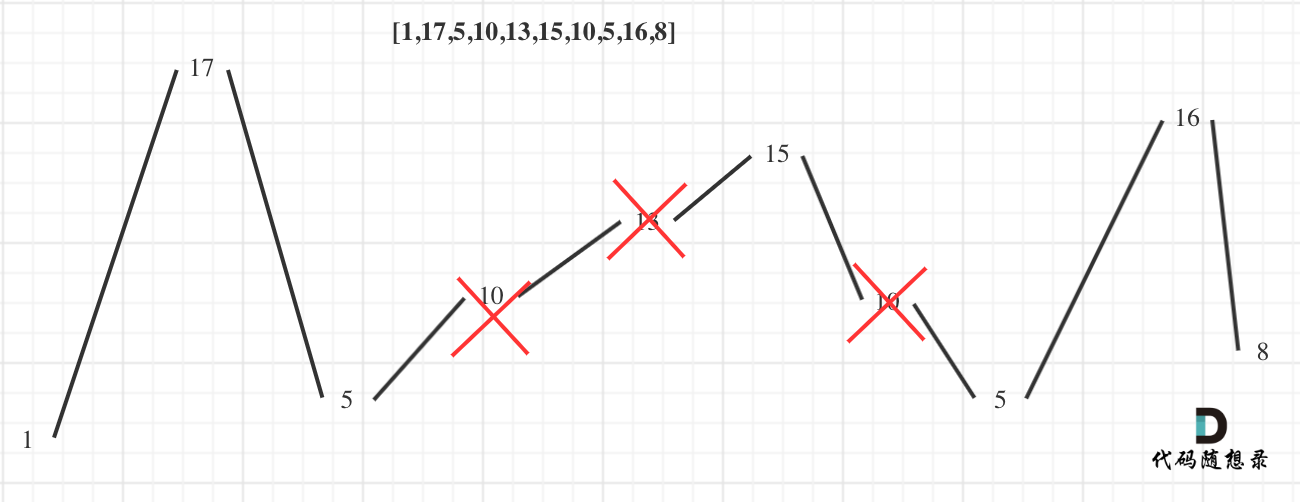
image.png
但是注意统计峰值的时候，数组最左面和最右面是最不好统计的。
例如序列[2,5]，它的峰值数量是2，如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
所以可以针对序列[2,5]，可以假设为[2,2,5]，这样它就有坡度了即preDiff = 0，如图：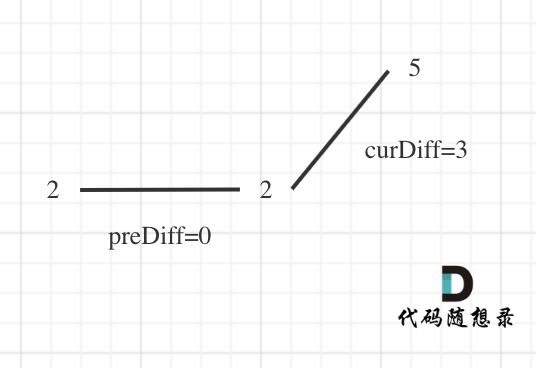
image.png
针对以上情形，result初始为1（默认最右面有一个峰值），此时curDiff > 0 && preDiff <= 0，那么result++（计算了左面的峰值），最后得到的result就是2（峰值个数为2即摆动序列长度为2）
也就是最开始默认峰值为0，最后默认最后有一个峰值，才方便处理开始和结尾。

  1. /**
  2.          * 贪心法：计算峰值即可
  3.          *
  4.          * @param nums
  5.          * @return
  6.          */
  7. public int wiggleMaxLength(int[] nums) {
  8.     if (nums.length <= 1) return nums.length;
  9.     int preDiff = 0; // 表示前一个峰值
  10.     int curDiff = 0; // 表示后一个峰值
  11.     int result = 1;  // 记录峰值的个数，默认最后一个数算一个峰值
  12.     for (int i = 0; i < nums.length - 1; i++) {
  13.         curDiff = nums[i + 1] - nums[i];    // 计算当前的峰值
  14.         if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
  15.             result++;
  16.             preDiff = curDiff;// 当前峰值赋值给前一个峰值
  17.         }
  18.     }
  19.     return result;
  20. }
  • 时间复杂度：$O(n)$

  • 空间复杂度：$O(1)$

    动态规划

    很容易可以发现，对于我们当前考虑的这个数，要么是作为山峰（即nums[i] > nums[i-1]），要么是作为山谷（即nums[i] < nums[i - 1]）。

  • 设dp状态dp[i][0]，表示考虑前i个数，第i个数作为山峰的摆动子序列的最长长度

  • 设dp状态dp[i][1]，表示考虑前i个数，第i个数作为山谷的摆动子序列的最长长度

则转移方程为：

  • dp[i][0] = max(dp[i][0], dp[j][1] + 1)，其中0 < j < i且nums[j] < nums[i]，表示将nums[i]接到前面某个山谷后面，作为山峰。
  • dp[i][1] = max(dp[i][1], dp[j][0] + 1)，其中0 < j < i且nums[j] > nums[i]，表示将nums[i]接到前面某个山峰后面，作为山谷。

初始状态：
由于一个数可以接到前面的某个数后面，也可以以自身为子序列的起点，所以初始状态为：dp[0][0] = dp[0][1] = 1。

  1. /**
  2.          * dp
  3.          *
  4.          * @param nums
  5.          * @return
  6.          */
  7. public int wiggleMaxLength(int[] nums) {
  8.     // 0 i 作为波峰的最大长度
  9.     // 1 i 作为波谷的最大长度
  10.     int[][] dp = new int[nums.length][2];
  11.     // 初始化
  12.     dp[0][1] = 1;
  13.     dp[0][0] = 1;
  14.     for (int i = 1; i < nums.length; i++) {
  15.         // 自己可以成为波峰或者波谷
  16.         dp[i][0] = dp[i][1] = 1;
  18.         for (int j = 0; j < i; j++) {
  20.             // 0表示波峰
  21.             if (nums[i] > nums[j]) {
  22.                 dp[i][0] = Math.max(dp[i][0], dp[j][1] + 1);
  23.             }
  25.             // 1表示波峰
  26.             if (nums[i] < nums[j]) {
  27.                 dp[i][1] = Math.max(dp[i][1], dp[j][0] + 1);
  28.             }
  29.         }
  30.     }
  31.     return Math.max(dp[nums.length - 1][1], dp[nums.length - 1][0]);
  32. }
  • 时间复杂度：$O(n^2)$
  • 空间复杂度：$O(n)$