双指针法

双指针法

双指针法解决三数之和，四数之和，五数之和…的问题。此类题目使用暴力解法的时间复杂度为O(n^n)，使用双指针法可以少依次for，为O(n ^ (n - 1))。

三数之和

题目描述

力扣连接🔗

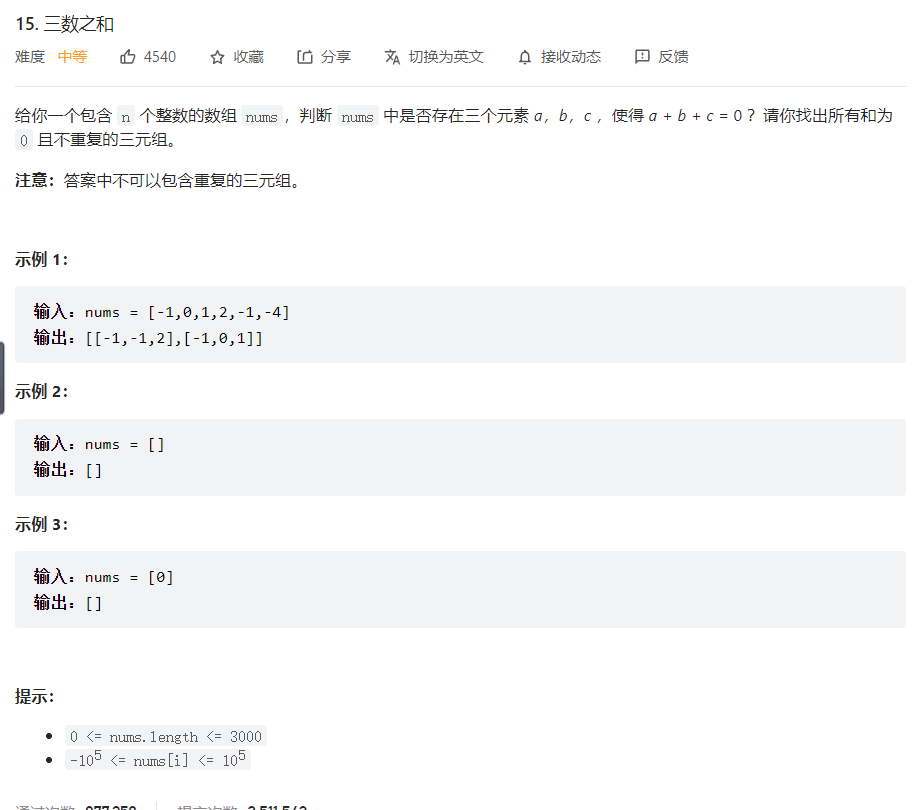
双指针法 - 图1

题目分析

使用hashMap来解决可以是使用 a + b 映射在map中，在查重 0 - (a + b) 的方法，但此时有大量的去重操作，使用2个for循环来寻找 a + b 此时时间复杂度位O(n^2)，所以此时可以考虑双指针法。

双指针动画效果：

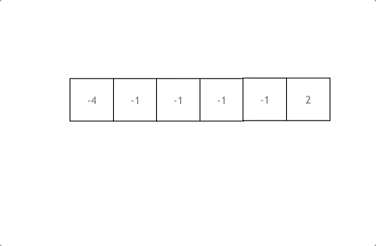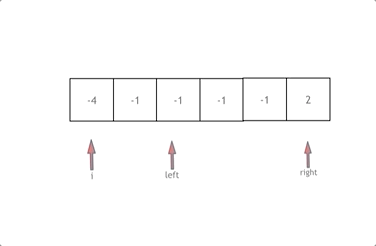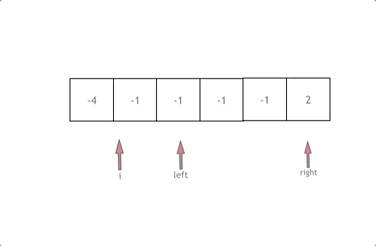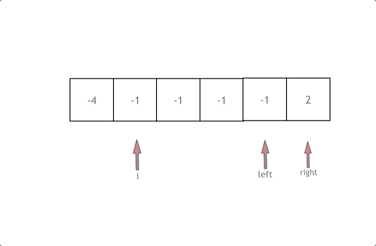
双指针法 - 图2

拿这个nums数组来举例，首先将数组排序，然后有一层for循环，i从下标0的地方开始，同时定一个下标left 定义在i+1的位置上，定义下标right 在数组结尾的位置上。

依然还是在数组中找到 abc 使得a + b +c =0，我们这里相当于 a = nums[i] b = nums[left] c = nums[right]。

接下来如何移动left 和right呢，如果nums[i] + nums[left] + nums[right] > 0 就说明此时三数之和大了，因为数组是排序后了，所以right下标就应该向左移动，这样才能让三数之和小一些。

如果 nums[i] + nums[left] + nums[right] < 0 说明此时三数之和小了，left 就向右移动，才能让三数之和大一些，直到left与right相遇为止。

此时的双指针法的时间复杂度也为 O(n^2)，但其中的去重更加方便。

大体的思路为：先将数组进行排序，使用一个for循环来遍历数组来确定一个数的值，使用左右指针再次遍历数组来进行查找（其中也涉及需要去重的操作）。

代码

class Solution {
    /**
     * 双指针法 + 排序
     *
     * @param nums
     * @return
     */
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        // 先将数组进行排序
        Arrays.sort(nums);
        // 循环遍历数组
        for (int i = 0; i < nums.length; i++) {
            // 排序后如果第一个数大于0，那么一定不可能凑出三元组
            if (nums[i] > 0) {
                return result;
            }
            // 两个数相等时，直接跳过这次判断，达到去重效果
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            int left = i + 1, right = nums.length - 1;
            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];
                // 大于0即右指针向左移动
                if (sum > 0) {
                    right--;
                }
                // 小于0即左指针向右移动
                else if (sum < 0) {
                    left++;
                }
                else{
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    // 去重，去重应该放在最后，放在最前面会漏掉0,0,0
                    while (right > left && nums[right - 1] == nums[right]) right--;
                    while (right > left && nums[left + 1] == nums[left]) left++;
                    // 再继续判断是否有相加为0的数
                    right--;
                    left++;
                }
            }
        }
        return result;
    }
}

四数之和

题目描述

力扣链接🔗

双指针法 - 图3

题目分析

思路和三数之和一致，只需要两次for循环遍历即可。

但是有一些细节需要注意，例如：不要判断nums[k] > target 就返回了，三数之和可以通过 nums[i] > 0 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。（大家亲自写代码就能感受出来）

四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下标作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是 $双指针法 - 图4$ #card=math&code=O%28n%5E2%29&id=jWOwT)，四数之和的时间复杂度是 $双指针法 - 图5$ #card=math&code=O%28n%5E3%29&id=vnl1E) 。

代码

 class Solution {
        /**
         * 双指针 + 排序
         *
         * @param nums
         * @param target
         * @return
         */
        public List<List<Integer>> fourSum(int[] nums, int target) {
            // 先将数组进行排序
            Arrays.sort(nums);
            List<List<Integer>> result = new ArrayList<>();
            for (int i = 0; i < nums.length; i++) {
                // 第一个数都大于target，那就不会有四元组相加等于target，此时不能使用判断，因为target存在负数
//                if (i > 0 && nums[i] > target) {
//                    return result;
//                }
                // 有重复数据，直接跳过，达到去重效果
                if (i > 0 && nums[i] == nums[i - 1]) {
                    continue;
                }
                for (int j = i + 1; j < nums.length; j++) {
                    // 此处不能判断第一个数大于target就返回，因为此时j不是最外层
//                    if (i > 0 && nums[i] > target) {
//                        return result;
//                    }
                    // 有重复数据，直接跳过，达到去重效果
                    // 注意此时 j > i + 1 ，不是 j > i ，否则漏掉2，2，2，2，2  8
                    if (j > i + 1 && nums[j] == nums[j - 1]) {
                        continue;
                    }
                    int left = j + 1, right = nums.length - 1;
                    while (left < right) {
                        int sum = nums[i] + nums[j] + nums[left] + nums[right];
                        if (sum > target) {
                            right--;
                        } else if (sum < target) {
                            left++;
                        } else {
                            result.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                            while (left < right && nums[right] == nums[right - 1]) right--;
                            while (left < right && nums[left] == nums[left + 1]) left++;
                            left++;
                            right--;
                        }
                    }
                }
            }
            return result;
        }
    }

何时不能使用此类方法

那么一样的道理，五数之和、六数之和等等都采用这种解法。

但是，例如：Map中讲到的两数之和，此时需要返回索引，但是我们此时需要排序之后进行双指针法，所以返回索引会很麻烦，此时就适合使用map的value存储索引。