题目描述

image.png

解题思路

本题的思路就是按照左边界排序，根据重复区间进行合并，每次合并后区间有边界取最大的右边界。
那么我按照左边界排序，排序之后局部最优：每次合并都取最大的右边界，这样就可以合并更多的区间了，整体最优：合并所有重叠的区间。
按照左边界从小到大排序之后，如果 intervals[i][0] < intervals[i - 1][1] 即intervals[i]左边界 < intervals[i - 1]右边界，则一定有重复，因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。
即：intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内，那么一定有重复！
这么说有点抽象，看图：（注意图中区间都是按照左边界排序之后了）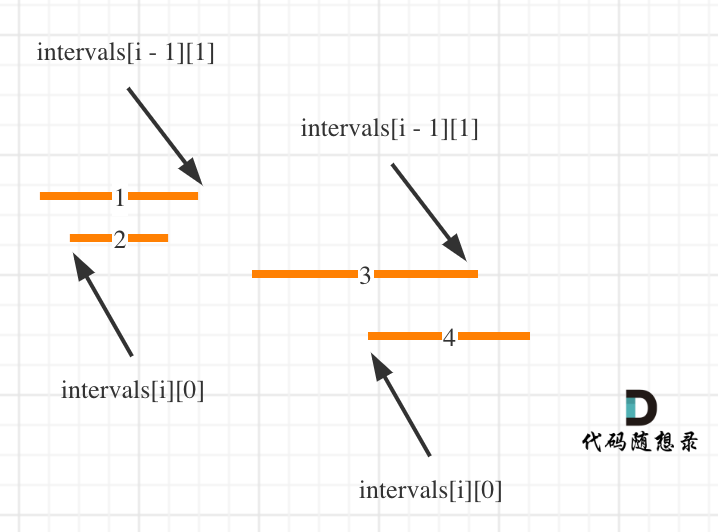
image.png知道如何判断重复之后，剩下的就是合并了，如何去模拟合并区间呢？
其实就是用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

  1. public int[][] merge(int[][] intervals) {
  2.     List<int[]> res = new ArrayList<>();
  3.     if (intervals.length == 0) return (int[][]) res.toArray();
  4.     Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));  // 根据左区间进行排序
  5.     int start = intervals[0][0];
  6.     for (int i = 1; i < intervals.length; i++) {
  7.         if (intervals[i][0] > intervals[i - 1][1]) {
  8.             res.add(new int[]{start, intervals[i - 1][1]}); // 不能合并，加入结果集
  9.             start = intervals[i][0];    // 更新开始区间
  10.         } else {
  11.             // 此时可以合并，则将右区间更新，此时不用加入结果集，下一次循环会判断这次区间
  12.             intervals[i][1] = Math.max(intervals[i - 1][1], intervals[i][1]);
  13.         }
  14.     }
  15.     res.add(new int[]{start, intervals[intervals.length - 1][1]});// 加入最后一个区间
  16.     return res.toArray(new int[res.size()][2]);
  17. }