题目描述

image.png

解题思路

二分法

排序数组中的搜索问题，首先想到 二分法 解决。
排序数组 nums 中的所有数字 target 形成一个窗口，记窗口的 左 / 右边界 索引分别为 left 和 right ，分别对应窗口左边 / 右边的首个元素。
本题要求统计数字 target 的出现次数，可转化为：使用二分法分别找到 左边界 left 和 右边界 right ，易得数字 target 的数量为 right - left - 1。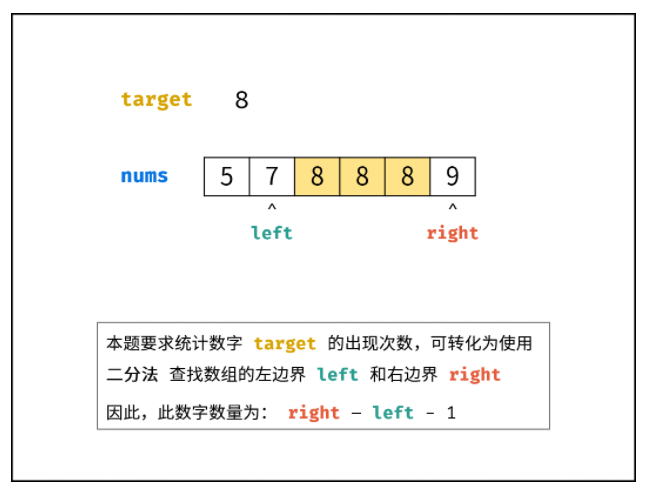
image.png
算法解析：

  • 初始化： 左边界 i = 0 ，右边界 j = len(nums) - 1。
  • 循环二分： 当闭区间 [i, j][i,j] 无元素时跳出；
    • 计算中点 m = (i + j) / 2m=(i+j)/2 （向下取整）；
    • 若 nums[m] < target ，则 target 在闭区间 [m + 1, j]中，因此执行 i = m + 1;
    • 若 nums[m] > target ，则 target 在闭区间 [i, m - 1] 中，因此执行 j = m - 1；
    • 若 nums[m] = target ，则右边界 right在闭区间 [m+1, j]中；左边界 left在闭区间 [i, m-1] 中。因此分为以下两种情况：
      • 若查找 右边界 right，则执行 i = m + 1 ；（跳出时 ii 指向右边界）
      • 若查找 左边界 left，则执行 j = m - 1；（跳出时 jj 指向左边界）
  • 返回值： 应用两次二分，分别查找 right和 left，最终返回 right - left - 1 即可。

效率优化：
以下优化基于：查找完右边界 right = iright=i 后，则 nums[j]nums[j] 指向最右边的 targettarget （若存在）。

查找完右边界后，可用 nums[j] = target 判断数组中是否包含 target，若不包含则直接提前返回 0 ，无需后续查找左边界。
查找完右边界后，左边界 left 一定在闭区间 [0, j]中，因此直接从此区间开始二分查找即可。
也就是通过2次二分法查找左右边界，在将左右边界进行计算。

  1. /**
  2.          * 二分法
  3.          *
  4.          * @param nums
  5.          * @param target
  6.          * @return
  7.          */
  8. public int search(int[] nums, int target) {
  9.     if (nums.length == 0) {
  10.         return 0;
  11.     }
  12.     int left = 0;
  13.     int right = nums.length - 1;
  14.     // 搜索有边界
  15.     while (left <= right) {
  16.         int mid = (left + right) / 2;
  17.         if (target >= nums[mid]) {
  18.             left = mid + 1;
  19.         } else right = mid - 1;
  20.     }
  22.     int edgeRight = left;  // 获取到右边界
  24.     // 若数组中无 target ，则提前返回
  25.     if (right > 0 && nums[right] != target) return 0;
  27.     left = 0;
  28.     right = nums.length - 1;
  29.     while (left <= right) {
  30.         int mid = (left + right) / 2;
  31.         if (target > nums[mid]) {
  32.             left = mid + 1;
  33.         } else right = mid - 1;
  34.     }
  36.     int edgeLeft = right;
  38.     return edgeRight - edgeLeft - 1;
  39. }
  • 时间复杂度 O(log N） ： 二分法为对数级别复杂度。
  • ** ： 几个变量使用常数大小的额外空间。

    哈希表

    1. /**
    2.        * 哈希表
    3.        * @param nums
    4.        * @param target
    5.        * @return
    6.        */
    7. public int search(int[] nums, int target) {
    8.   HashMap<Integer, Integer> map = new HashMap<>();
    9.   for (int i = 0; i < nums.length; i++) {
    10.       map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
    11.   }
    12.   return map.get(target) == null ? 0 : Integer.valueOf(map.get(target));
    13. }