算法解析

归并排序体现了 “分而治之” 的算法思想，具体为：
「分」： 不断将数组从 中点位置 划分开，将原数组的排序问题转化为子数组的排序问题；
「治」： 划分到子数组长度为 1 时，开始向上合并，不断将 左右两个较短排序数组 合并为 一个较长排序数组，直至合并至原数组时完成排序；
如下图所示，为数组 [7,3,2,6,0,1,5,4] 的归并排序过程。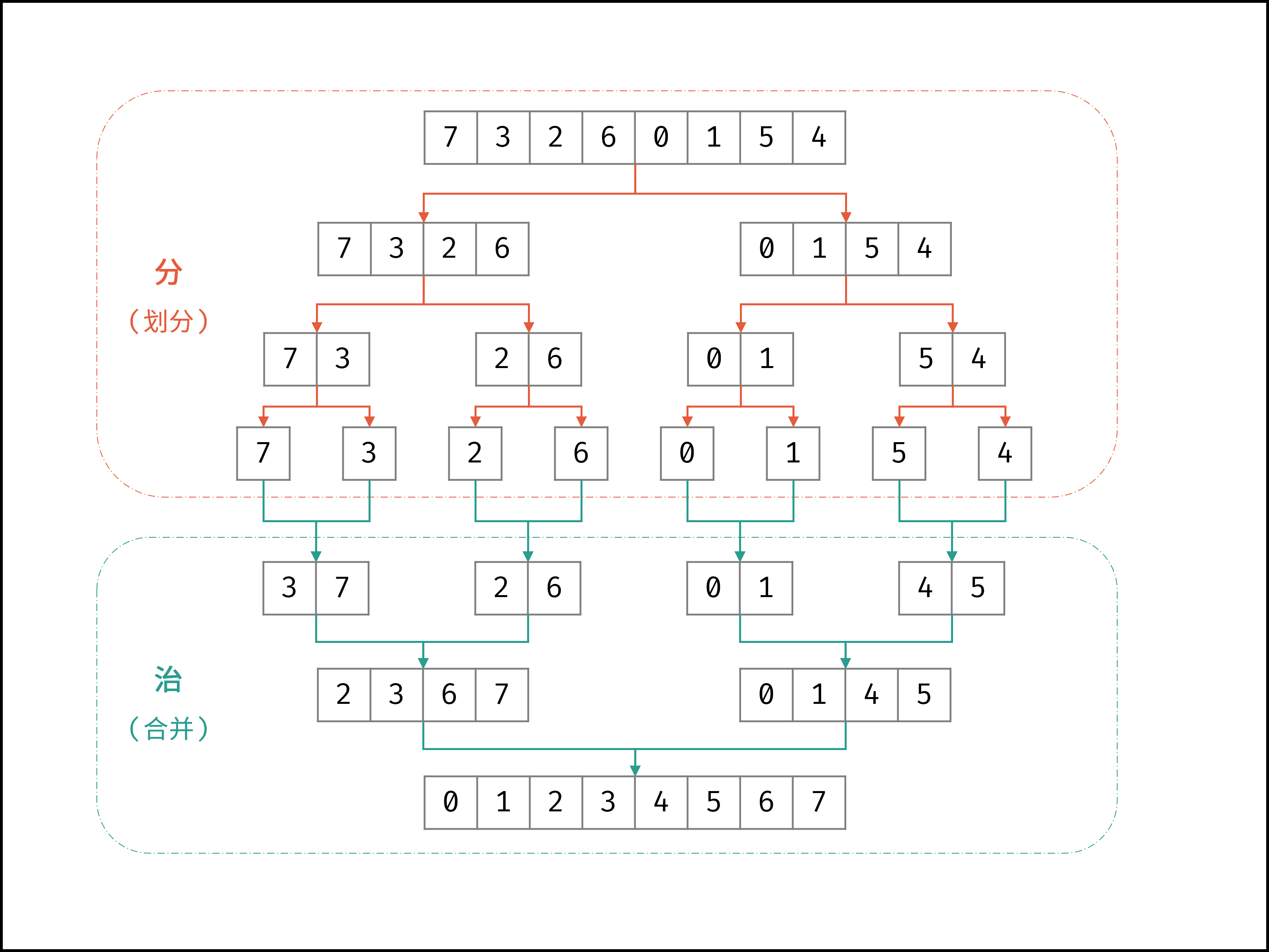

算法流程

递归划分：
计算数组中点 m ，递归划分左子数组 merge_sort(l, m) 和右子数组 merge_sort(m + 1, r) ；
当 l≥r 时，代表子数组长度为 1 或 0 ，此时 终止划分 ，开始合并；
合并子数组：
暂存数组 nums 闭区间 [l, r] 内的元素至辅助数组 tmp ；
循环合并： 设置双指针 i , j 分别指向 tmp 的左 / 右子数组的首元素；
注意： nums 子数组的左边界、中点、右边界分别为 l , m , r ，而辅助数组 tmp 中的对应索引为 0 , m - l , r−l ；
当 i == m - l + 1 时： 代表左子数组已合并完，因此添加右子数组元素 tmp[j] ，并执行 j = j + 1 ；
否则，当 j == r - l + 1 时： 代表右子数组已合并完，因此添加左子数组元素 tmp[i] ，并执行 i = i + 1 ；
否则，当 tmp[i]≤tmp[j] 时： 添加左子数组元素 tmp[i] ，并执行 i = i + 1 ；
否则（即当 tmp[i]>tmp[j] 时）： 添加右子数组元素 tmp[j]tmp[j] ，并执行 j = j + 1 ；如下动图所示，为数组 [7,3,2,6] 的归并排序过程。

/**
 * 归并排序
 */
public class MergeSortTest {
    public static void main(String[] args) {
        // 调用
        int[] nums = {3, 4, 1, 5, 2, 1};
        MergeSortTest mergeSortTest = new MergeSortTest();
        mergeSortTest.mergeSort(nums, 0, nums.length - 1);
        for (int num : nums) {
            System.out.print(num);
        }
    }
    /**
     * 归并排序
     *
     * @param nums
     * @param l
     * @param r
     */
    void mergeSort(int[] nums, int l, int r) {
        // 终止条件
        if (l >= r) {
            return;
        }
        int mid = (l + r) / 2;
        mergeSort(nums, l, mid);
        mergeSort(nums, mid + 1, r);
        int[] tmp = new int[r - l + 1]; // 暂时保存元素
        for (int i = l; i <= r; i++) {
            tmp[i - l] = nums[i];
        }
        int i = 0, j = mid - l + 1;
        for (int k = l; k <= r; k++) {
            if (i == mid - l + 1) {
                nums[k] = tmp[j++];
            } else if (j == r - l + 1 || tmp[i] <= tmp[j]) {
                nums[k] = tmp[i++];
            } else if (tmp[i] > tmp[j]) {
                nums[k] = tmp[j++];
            }
        }
    }
}