题目描述

image.png

解题思路

哈希法

  1. public int majorityElement(int[] nums) {
  2.     Map<Integer, Integer> map = new HashMap<>();
  3.     for (int i = 0; i < nums.length; i++) {
  4.         map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
  5.     }
  7.     for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
  8.         if (entry.getValue() > nums.length / 2) return entry.getKey();
  9.     }
  11.     return 0;
  12. }

排序法

由于一定有众数，且众数占数组长度一半，所以排序之后取中间值。

  1. public int majorityElement(int[] nums) {
  2.     Arrays.sort(nums);
  3.     return nums[nums.length / 2];
  4. }

摩尔投票法

推论一： 若记 众数 的票数为 +1 ，非众数 的票数为 -1 ，则一定有所有数字的 票数和 > 0 。
推论二： 若数组的前 a 个数字的 票数和 =0 ，则 数组剩余 (n-a) 个数字的 票数和一定仍 >0 ，即后 (n-a) 个数字的 众数仍为 x 。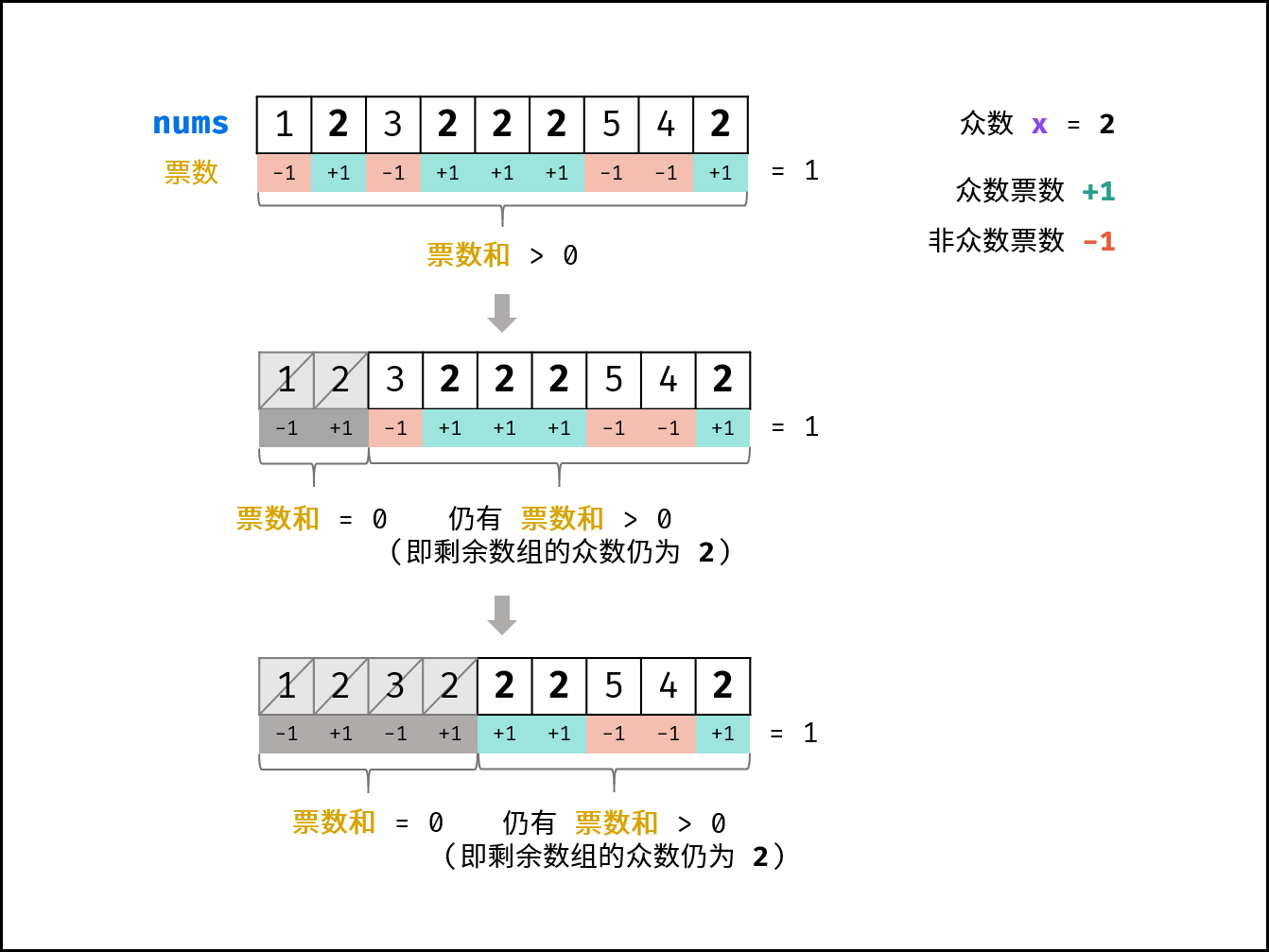
image.png
根据以上推论，记数组首个元素为n，众数为α，遍历并统计票数。
当发生票数和=0时，剩余数组的众数一定不变，这是由于:

  • 当n1= a :抵消的所有数字，有一半是众数α。
  • 当n1≠a :抵消的所有数字，众数α的数量最少为0个，最多为一半。

利用此特性，每轮假设发生票数和=0都可以缩小剩余数组区间。当遍历完成时，最后一轮假设的数字即为众数。

也就是把第一个数字当作备选者，遍历数组，如果相同则选举加一，如果不相同则选举减一，当选举为0的时候，此时就需要重新选择备选者进行投票。

  1. // 投票法
  2. public int majorityElement(int[] nums) {
  3.     int x = 0, votes = 0;
  4.     for (int num : nums) {
  5.         if (votes == 0) x = num;
  6.         if (num == x) votes++;
  7.         else votes--;
  8.     }
  10.     // 如果不存在众数，需要遍历x进行验证本题说明了存在众数
  11.     /*int count = 0;
  12.             for (int num : nums) {
  13.                 if (x == num) count++;
  14.             }
  15.             if (count > nums.length / 2) return x;*/
  17.     return x;
  18. }

image.png

扩展

此时如果大于数组长度一半的众数不一定存在，那么最后一个数就不一定是需要找的众数，所以还需要遍历一次数字，使用计数器技术到底该数是不是需要找的数。

  1. // 投票法
  2. public int majorityElement(int[] nums) {
  3.     int x = 0, votes = 0;
  4.     for (int num : nums) {
  5.         if (votes == 0) x = num;
  6.         if (num == x) votes++;
  7.         else votes--;
  8.     }
  10.     // 如果不存在众数，需要遍历x进行验证本题说明了存在众数
  11.     int count = 0;
  12.     for (int num : nums) {
  13.         if (x == num) count++;
  14.     }
  15.     if (count > nums.length / 2) return x;
  17.     return x;
  18. }