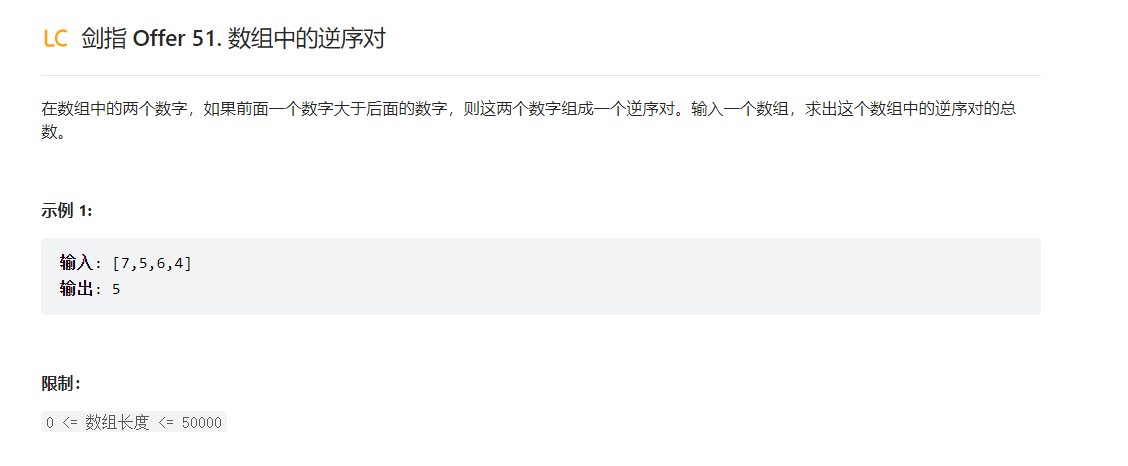
题目描述

解题思路

回溯（超时）

int count = 0;
LinkedList<Integer> path = new LinkedList<>();
public void traversal(int[] nums, int startIndex, boolean[] used) {
    if (path.size() == 2) {
        count++;
        return;
    }
    for (int i = startIndex; i < nums.length; i++) {
        if (used[i] == true) continue;
        if (!path.isEmpty() && Integer.compare(nums[i], path.getLast()) >= 0) continue;
        used[i] = true;
        path.add(nums[i]);
        traversal(nums, i + 1, used);
        path.remove(path.size() - 1);
        used[i] = false;
    }
}

归并排序中处理

归并排序思路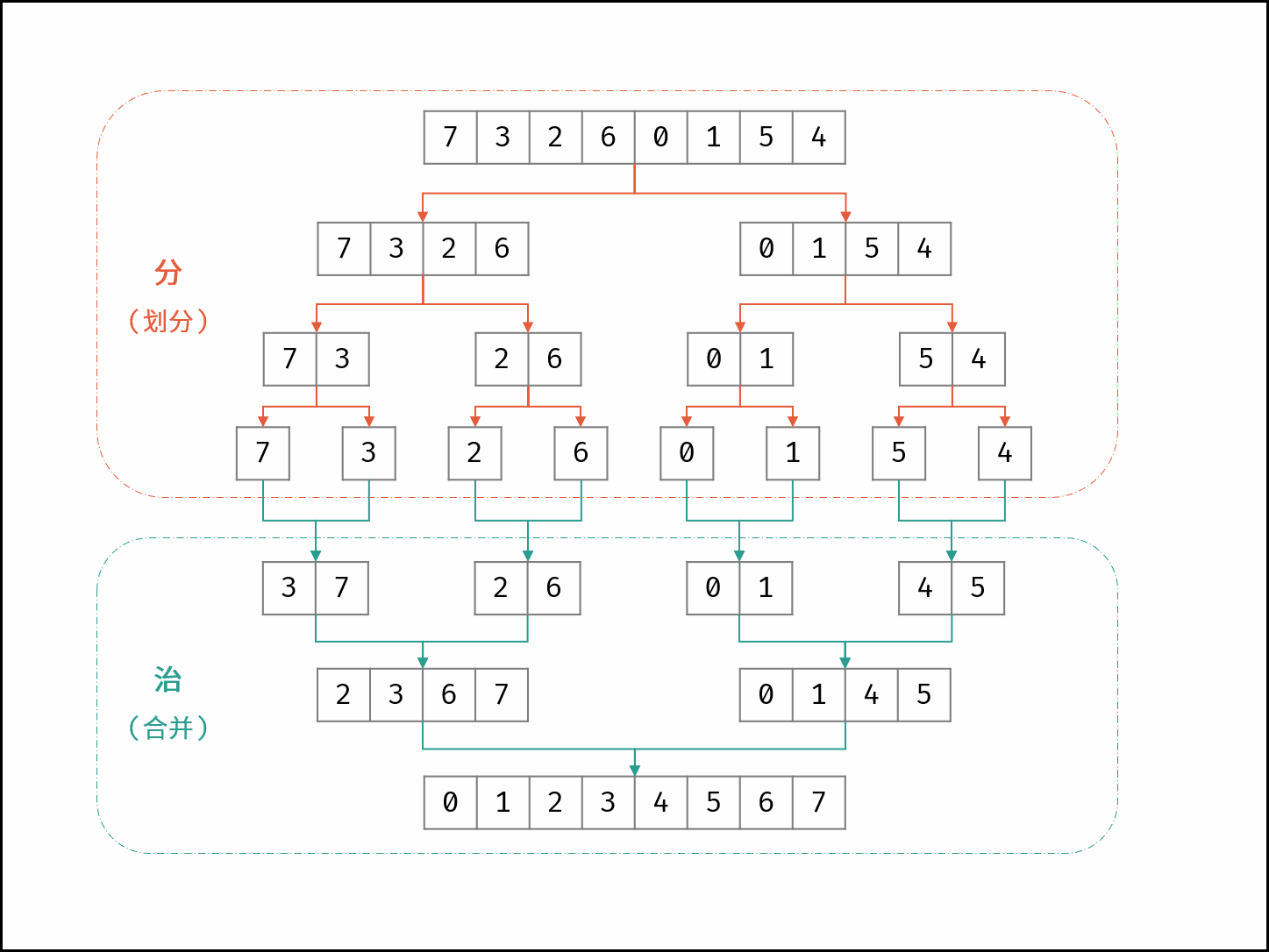

此时在合并过程中可以进行比较
例如左边的i为2，右边的j为0，此时i为左边最小的数字，所以左边数字在i之后的数字都是逆序对，此时j++，并把j的数加入排好序的数组。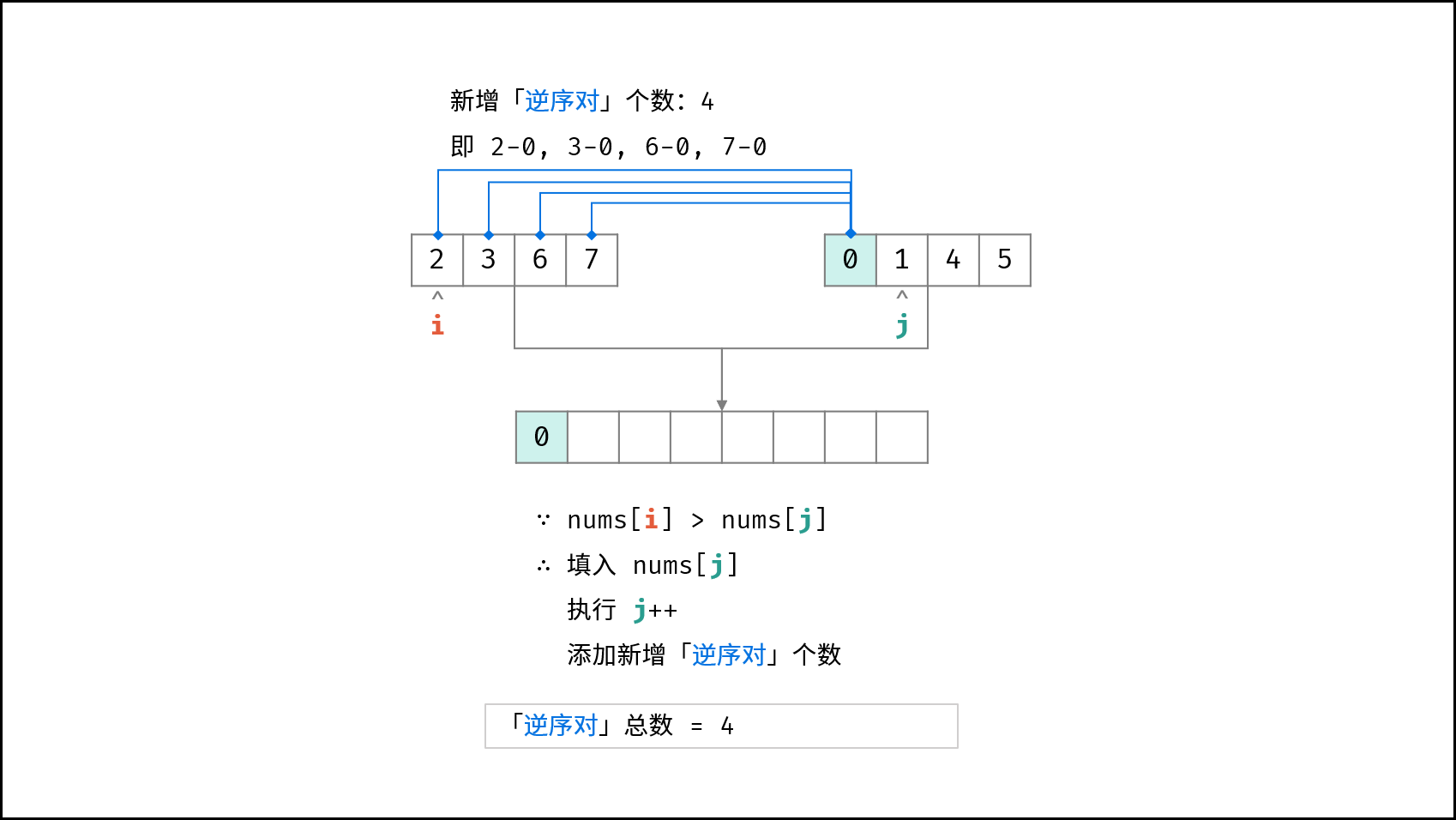

此时也增加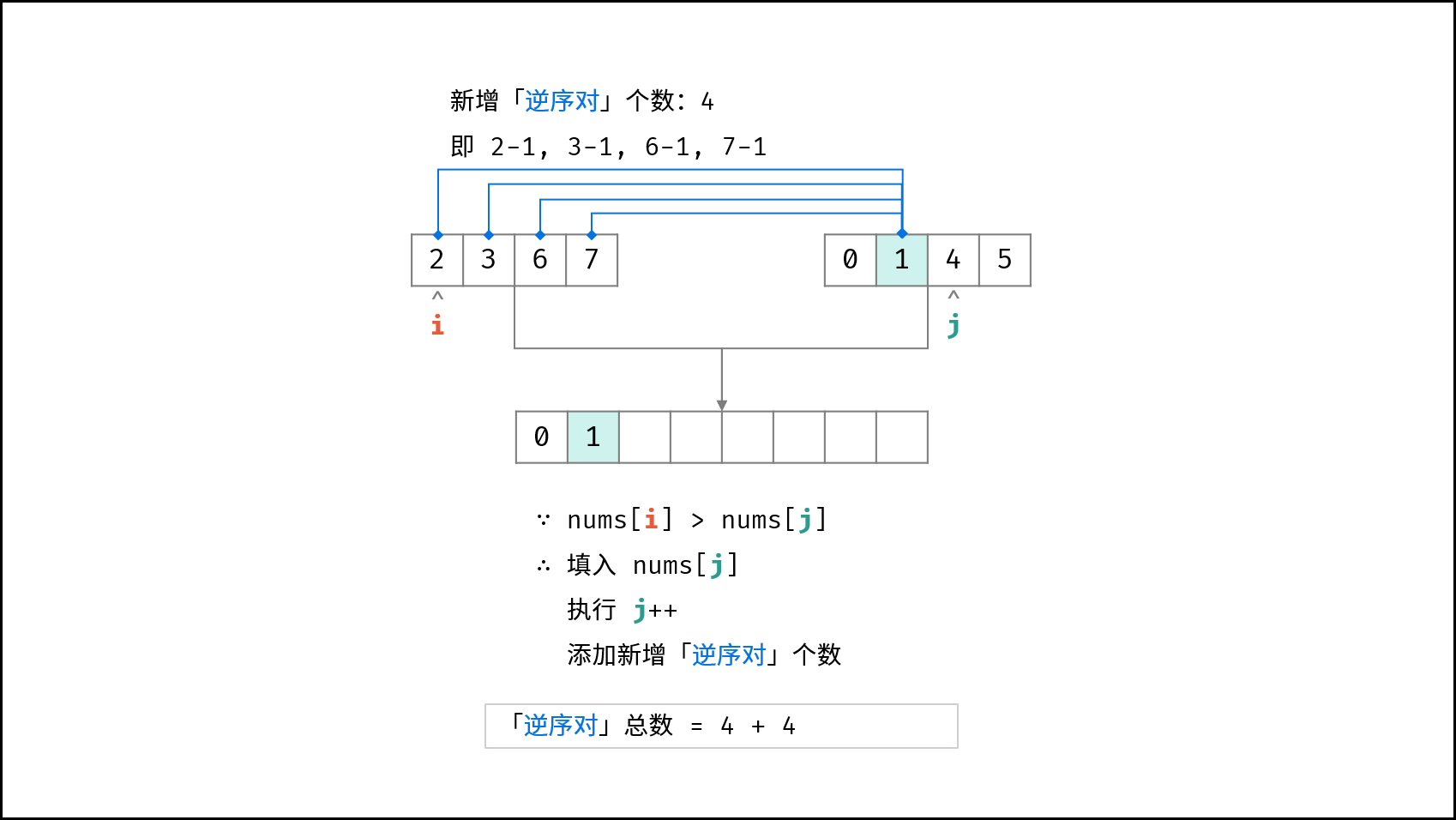

当i的数小于j的数的时候i加入排好序的数组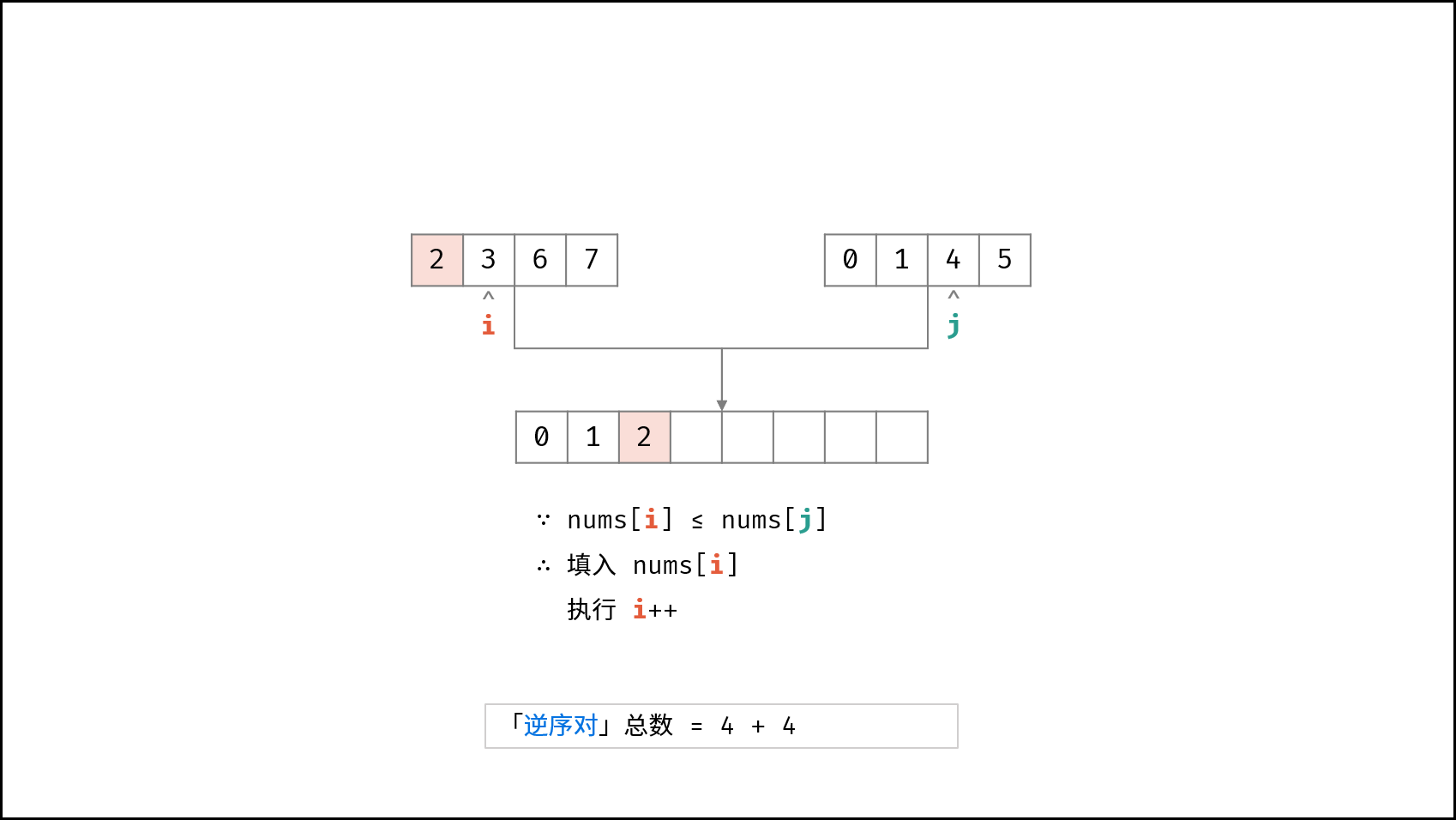

算法流程：

• 终止条件

当有边界小于等于左边界的时候，此时就应该停止递归分割。

• 递归划分： 计算数组中点 mm ，递归划分左子数组 merge_sort(l, m) 和右子数组 merge_sort(m + 1, r) ；
• 合并与逆序对统计：

暂存数组 numsnums 闭区间 [l, r] 内的元素至辅助数组 tmp ；
循环合并： 设置双指针 ii , jj 分别指向左 / 右子数组的首元素；
当 i = m + 1时： 代表左子数组已合并完，因此添加右子数组当前元素 tmp[j] ，并执行 j = j + 1 ；
否则，当 j = r + 1 时： 代表右子数组已合并完，因此添加左子数组当前元素 tmp[i] ，并执行 i = i + 1 ；
否则，当 tmp[i]≤tmp[j] 时： 添加左子数组当前元素 tmp[i]，并执行 i = i + 1；
否则（即 tmp[i] > tmp[j]）时： 添加右子数组当前元素 tmp[j]，并执行 j = j + 1 ；此时构成 m - i + 1 个「逆序对」，统计添加至 res ；

• 返回值： 返回直至目前的逆序对总数 resres ；

public int reversePairs(int[] nums) {
    if (nums.length == 1) return 0;
    this.nums = nums;
    tmp = new int[nums.length];
    return mergeSort(0, nums.length - 1);
}
int[] nums, tmp;
public int mergeSort(int l, int r) {
    if (l >= r) {
        return 0;
    }
    // 递归划分
    int mid = (r + l) / 2;
    int res = mergeSort(l, mid) + mergeSort(mid + 1, r);
    for (int i = l; i <= r; i++) {
        tmp[i] = nums[i];
    }
    // 开始合并
    int i = l, j = mid + 1;
    for (int k = l; k <= r; k++) {
        if (i == mid + 1) {
            nums[k] = tmp[j++];
            // 注意使用tmp来比较，num会被覆盖
        } else if (j == r + 1 || tmp[j] >= tmp[i]) {
            nums[k] = tmp[i++];
        } else {
            nums[k] = tmp[j++];
            res += mid - i + 1;
        }
    }
    return res;
}