简介

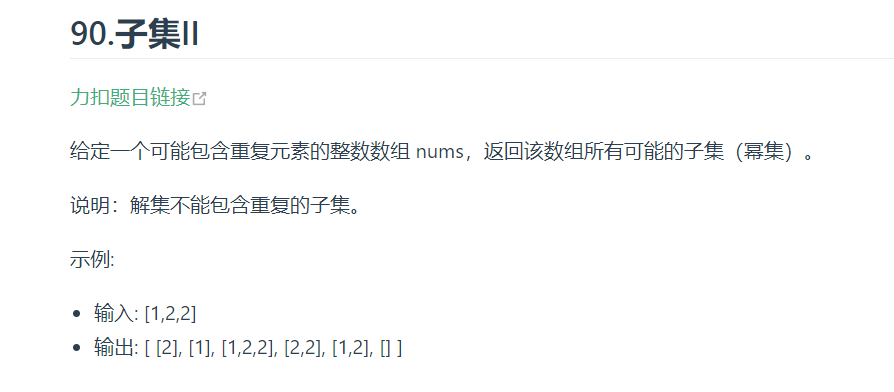
其实子集也是一种组合问题，因为它的集合是无序的，子集{1,2} 和子集{2,1}是一样的。

时间复杂度：O(2^n)，因为每一个元素的状态无外乎取与不取，所以时间复杂度为O(2^n)
空间复杂度：O(n)，递归深度为n，所以系统栈所用空间为O(n)，每一层递归所用的空间都是常数级别，注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为O(n)

78.子集

题目描述

解题思路
递归函数参数

res，path，因为不重复选取所以需要startIndex

递归终止条件

那么什么时候剩余集合为空呢？就是startIndex已经大于数组的长度了，就终止了，因为没有元素可取（加不加都可以，for中已经判断了）

单层搜索逻辑

求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。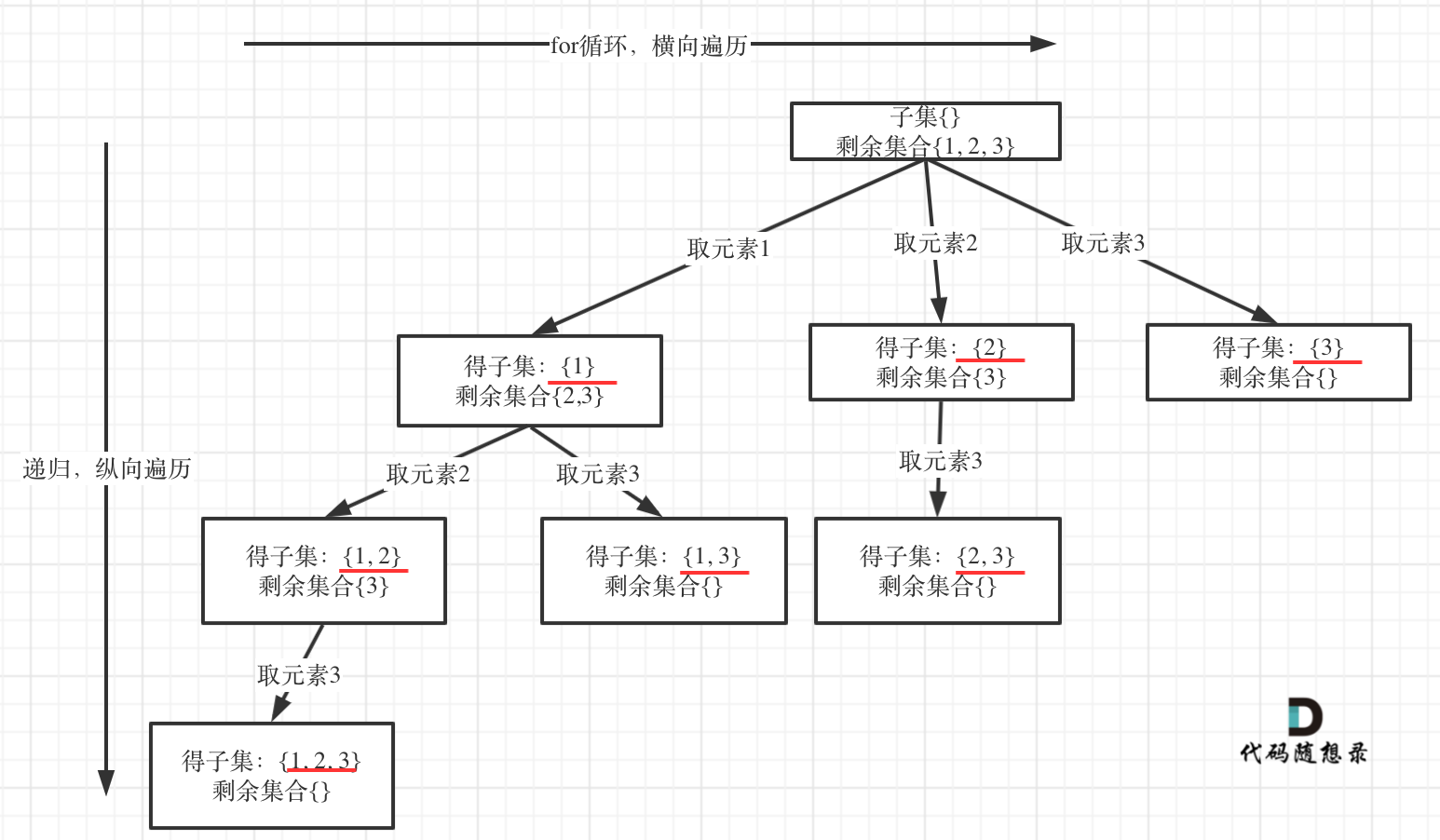

public List<List<Integer>> subsets(int[] nums) {
    if (nums.length == 0) {
        return res;
    }
    backtracking(nums, 0);
    return res;
}
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public void backtracking(int[] nums, int startIndex) {
    // 收集子集，要放在终止添加的上面，否则会漏掉自己
    res.add(new ArrayList<>(path)); // 此时时每层递归都要将路径加入结果集，因为求得时子集
    if (startIndex >= nums.length) {    // 可以不同加终止条件，后面for也满足
        return;
    }
    for (int i = startIndex; i < nums.length; i++) {
        path.add(nums[i]);
        backtracking(nums, i + 1);
        path.removeLast();  // 回溯
    }
}

90.子集II

题目描述

解题思路

注意题目给的是包含重复元素，但结果不能包含重复元素，所以可以使用树层去重，本题和78.子集相差不大。（注意树层去重需要排序）

public List<List<Integer>> subsetsWithDup(int[] nums) {
    if (nums.length == 0) {
        return res;
    }
    Arrays.sort(nums);  // 必须要进行排序，才能达到去重效果
    backtracking(nums, 0, new boolean[nums.length]);
    return res;
}
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public void backtracking(int[] nums, int startIndex, boolean[] used) {
    res.add(new ArrayList<>(path));
    if (startIndex >= nums.length) {
        return;
    }
    for (int i = startIndex; i < nums.length; i++) {
        if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {   // 已经被选择
            continue;
        } else { // 注意不能放在if里面，以为if里面将 i > 0 之后才会进行判断
            path.add(nums[i]);
            used[i] = true;
            backtracking(nums, i + 1, used);
            used[i] = false;
            path.removeLast();
        }
    }
}

树层去重还可以使用哈希表

可以使用set针对同一父节点本层去重，但子集问题一定要排序，为什么呢？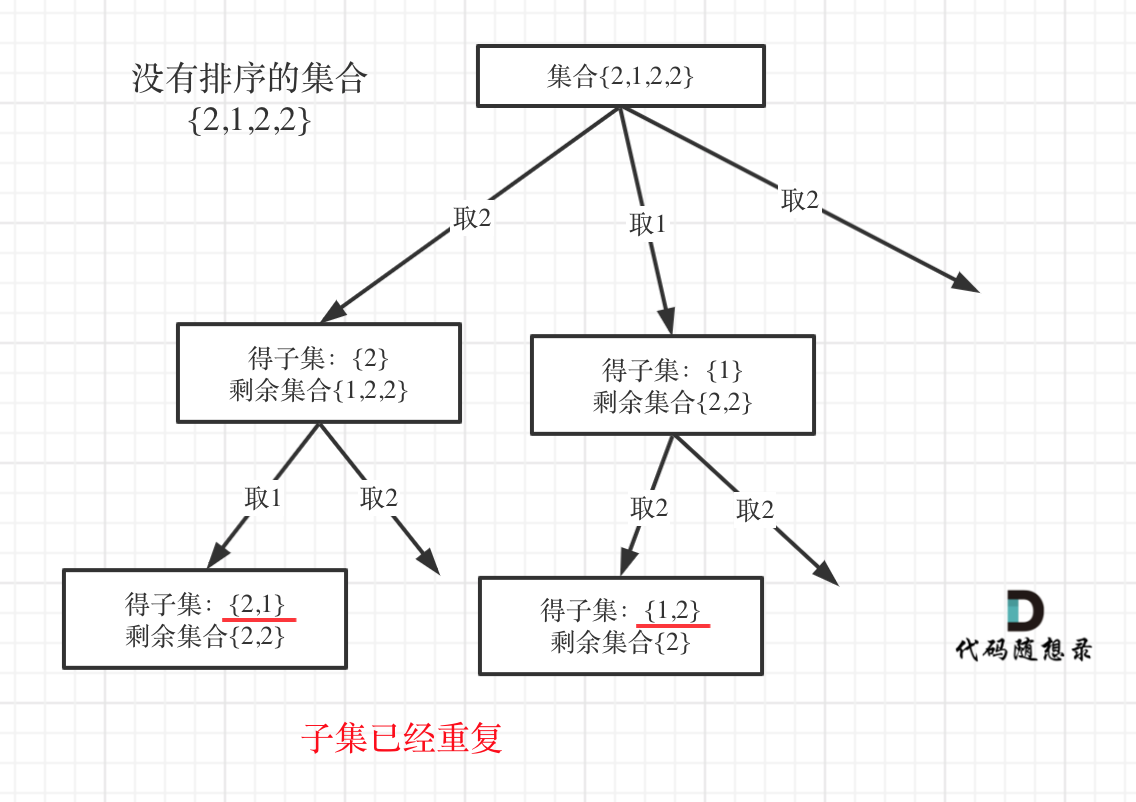

public List<List<Integer>> subsetsWithDup(int[] nums) {
    Arrays.sort(nums);
    //            backtracking(nums, new boolean[nums.length], 0);
    // set做法
    backtracking(nums, 0);
    return res;
}
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
/**
         * 使用set
         *
         * @param nums
         * @param startIndex
         */
public void backtracking(int[] nums, int startIndex) {
    res.add(new ArrayList<>(path));
    if (startIndex >= nums.length) {
        return;
    }
    Set<Integer> set = new HashSet<>();
    for (int i = startIndex; i < nums.length; i++) {
        if (!set.isEmpty() && set.contains(nums[i])) continue;
        set.add(nums[i]);
        path.add(nums[i]);
        backtracking(nums, i + 1);
        path.removeLast();
    }
}

491.递增子序列

题目描述

解题思路

在90.子集II中我们是通过排序，再加一个标记数组来达到去重的目的。
而本题求自增子序列，是不能对原数组经行排序的，排完序的数组都是自增子序列了。
所以不能使用之前的去重逻辑！

递归函数参数

不能重复选取，使用startIndex

终止条件

本题其实类似求子集问题，也是要遍历树形结构找每一个节点，所以和回溯算法：求子集问题！一样，可以不加终止条件，startIndex每次都会加1，并不会无限递归。
但本题收集结果有所不同，题目要求递增子序列大小至少为2。

单层搜索逻辑

在图中可以看出，同一父节点下的同层上使用过的元素就不能在使用了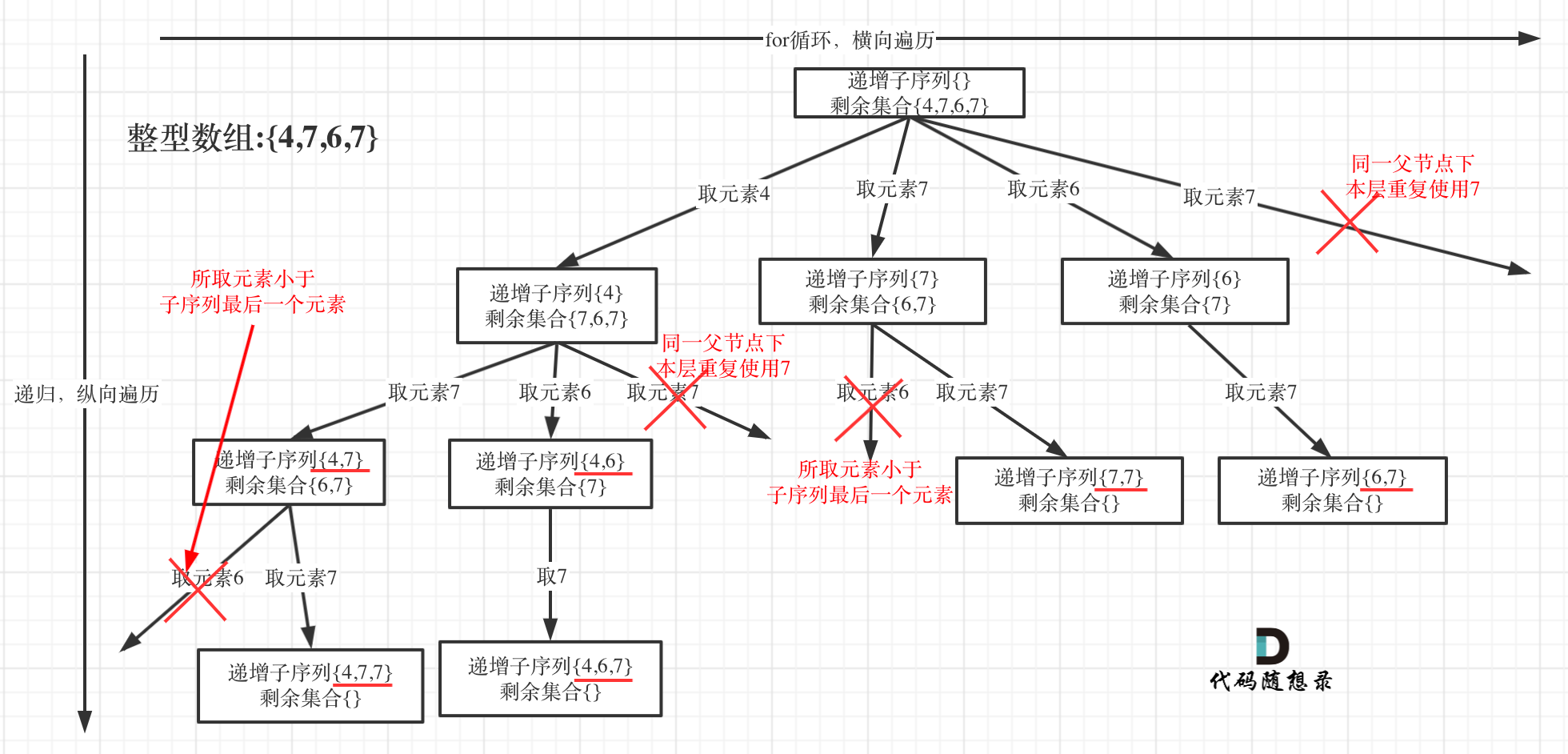

使用map表示哈希表

public List<List<Integer>> findSubsequences(int[] nums) {
    if (nums.length == 0) {
        return res;
    }
    backtracking(nums, 0);
    return res;
}
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
/**
         * 使用hash法来进行判重
         *
         * @param nums
         * @param startIndex
         */
public void backtracking(int[] nums, int startIndex) {
    if (path.size() > 1) {
        res.add(new ArrayList<>(path)); // 取树枝上的值
    }
    Map<Integer, Integer> map = new HashMap<>();    // 用来判断本层是否重复使用，每次for之前，也就是每层都需要重新使用一个map来判断
    for (int i = startIndex; i < nums.length; i++) {
        if (!path.isEmpty() && nums[i] < path.getLast()) {  // 如果2个数不是递增，跳过此次选择
            continue;
        }
        if (map.getOrDefault(nums[i], 0) > 0) { // 本层中已经取过此元素
            continue;
        }
        map.put(nums[i], map.getOrDefault(nums[i], 0) + 1); // 去过就放入map中
        path.add(nums[i]);
        backtracking(nums, i + 1);
        path.removeLast();  // 回溯
    }
}

使用数组来表示哈希表，节约空间

public List<List<Integer>> findSubsequences(int[] nums) {
    backtracking(nums, 0);
    return res;
}
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public void backtracking(int[] nums, int startIndex) {
    // 大小至少为2才可以算作一个递增子序列
    if (path.size() > 1) {
        res.add(new ArrayList<>(path));
    }
    if (startIndex >= nums.length) {
        return;
    }
    // 使用数组来表示哈希表
    // 由于题目给的数是在[-100,100]之间，所以申请201个单元
    int[] used = new int[201];
    for (int i = startIndex; i < nums.length; i++) {
        // 不是递增序列或者同一层出现过，直接跳过此次选取
        // 注意是path的最后一个元素进行比较
        if ((!path.isEmpty() && nums[i] < path.getLast()) || used[nums[i] + 100] == 1) continue;
        path.add(nums[i]);
        used[nums[i] + 100] = 1;
        backtracking(nums, i + 1);
        // 错误操作：此时的哈希表表只代表本层是否使用过，和下一层无关
        // 所以下一次回溯时，和本层是否选取无关系，所以不能回溯
        // 注意和前面排序之后使用used区分
        // used时整个所有数都是用used来判断，所以有关系
        // used[nums[i] + 100] = 0;
        path.removeLast();
    }
}