题目描述

🔗

解题思路

删除节点并不能简单删除，而是需要重构树。

递归法

  • 确定递归函数参数以及返回值

说道递归函数的返回值，在搜索树中的插入操作(opens new window)中通过递归返回值来加入新节点， 这里也可以通过递归返回值删除节点。

  • 确定终止条件

遇到空返回，其实这也说明没找到删除的节点，遍历到空节点直接返回了

  • 单层处理逻辑
    • 第一种情况：没找到删除的节点，遍历到空节点直接返回了
    • 找到删除的节点
      • 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
      • 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
      • 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
      • 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

第五种情况：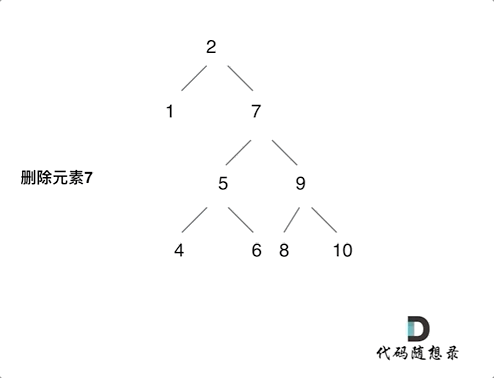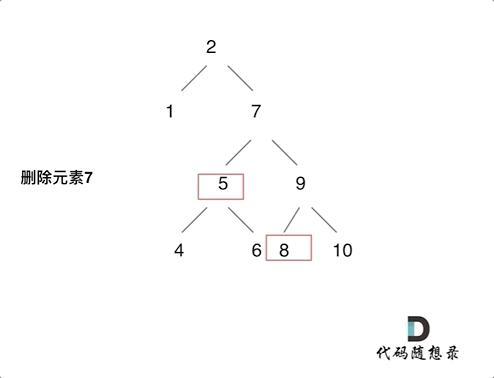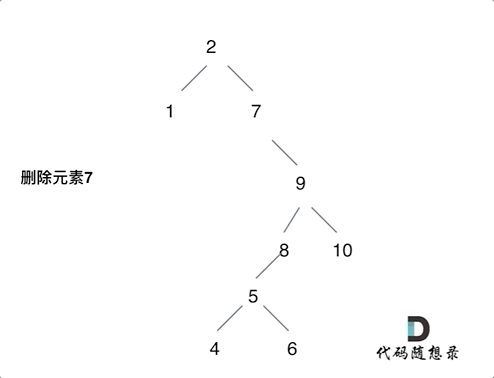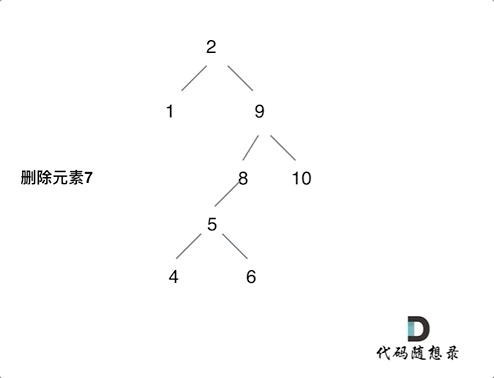
删除二叉搜索树中的节点 - 图1

  1. public TreeNode deleteNode(TreeNode root, int key) {
  2.     if (root == null) {
  3.         return null;
  4.     }
  6.     if (root.val == key) {
  7.         // 情况一：左为空，右不为空
  8.         if (root.left == null && root.right != null) return root.left;
  9.         // 情况二：左不为空，右为空
  10.         else if (root.left != null && root.right == null) return root.right;
  11.         // 情况三：左右都为空，直接删除
  12.         else if (root.left == null && root.right == null) return null;
  13.         // 情况四：左右都不为空，那么左节点放到右节点的最左边的节点
  14.         else {
  15.             // 找到右子树的最左边的节点
  16.             TreeNode cur = root.right;
  17.             while (cur.left != null) {
  18.                 cur = cur.left;
  19.             }
  20.             // 赋值过去
  21.             cur.left = root.left;
  22.             // 删除该节点，返回右子树
  23.             root = root.right;
  24.             return root;
  25.         }
  26.     }
  28.     // 根据二叉搜索树的性质进行递归，并接收返回值
  29.     if (root.val > key) root.left = deleteNode(root.left, key);
  30.     if (root.val < key) root.right = deleteNode(root.right, key);
  31.     return root;
  32. }

迭代法

  1. // 迭代法
  2. public TreeNode deleteNode(TreeNode root, int key) {
  3.     if (root == null) {
  4.         return null;
  5.     }
  7.     TreeNode pre = null;
  8.     TreeNode cur = root;
  9.     while (cur != null) {
  10.         if (cur.val == key) break;
  11.         // 一定放在break后面，因为pre是cur的父节点
  12.         pre = cur;
  13.         if (cur.val > key) cur = cur.left;
  14.         else if (cur.val < key) cur = cur.right;
  15.     }
  17.     if (pre == null) {
  18.         return deleteNodes(cur);
  19.     }
  21.     // 得知道是删除那个节点（也就是知道cur是pre的左节点还是右节点）
  22.     if (pre.left != null && pre.left.val == key) {
  23.         pre.left = deleteNodes(cur);
  24.     }
  26.     if (pre.right != null && pre.right.val == key) {
  27.         pre.right = deleteNodes(cur);
  28.     }
  30.     return root;
  31. }
  33. // 删除节点的4种情况（迭代的删除节点）
  34. public TreeNode deleteNodes(TreeNode target) {
  35.     if (target == null) return target;
  36.     if (target.left == null) return target.right;
  37.     if (target.right == null) return target.left;
  39.     TreeNode cur = target.right;
  40.     while (cur.left != null) {
  41.         cur = cur.left;
  42.     }
  44.     cur.left = target.left;
  45.     return target.right;
  46. }