题目描述

解题思路

如何套入为0-1背包呢？
此题推导公式：
left表示正号的一组，right表示负号的一组。
此时left + right = sum（总个数）
left - (sum - left) = target 即 left = (target + sum) / 2;
由于target和sum固定，所以转化为在固定背包中，找出left的种类数。
此时0-1背包的使用环境也就出来了！！！
此时问题就转化为，装满容量为x背包，有几种方法。
步骤：
此时还有2中情况不满足：
大家看到(S + sum) / 2 应该担心计算的过程中向下取整有没有影响。
例如sum 是5，S是2的话其实就是无解的，所以：
if ((S + sum) % 2 == 1) return 0; // 此时没有方案
同时如果 S的绝对值已经大于sum，那么也是没有方案的。
if (Math.abs(S) > sum) return 0; // 此时没有方案

• 确定dp数组以及下标的含义

dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

• 确定递推公式

不考虑nums[i]的情况下，填满容量为j - nums[i]的背包，有dp[j - nums[i]]种方法。
那么只要搞到nums[i]的话，凑成dp[j]就有dp[j - nums[i]] 种方法。
例如：dp[j]，j 为5，

• 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 dp[5]。
• 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 dp[5]。
• 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 dp[5]
• 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 dp[5]
• 已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 dp[5]

那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。

类似组合求总数的dp公式也是这种！！！

• dp数组如何初始化

dp[0] = 1，理论上也很好解释，装满容量为0的背包，有1种方法，就是装0件物品。
如何初始化为0，那么后面推到出来都是0。

• 遍历顺序

滚动数组注意倒序遍历。

• 举例推导dp数组

输入：nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4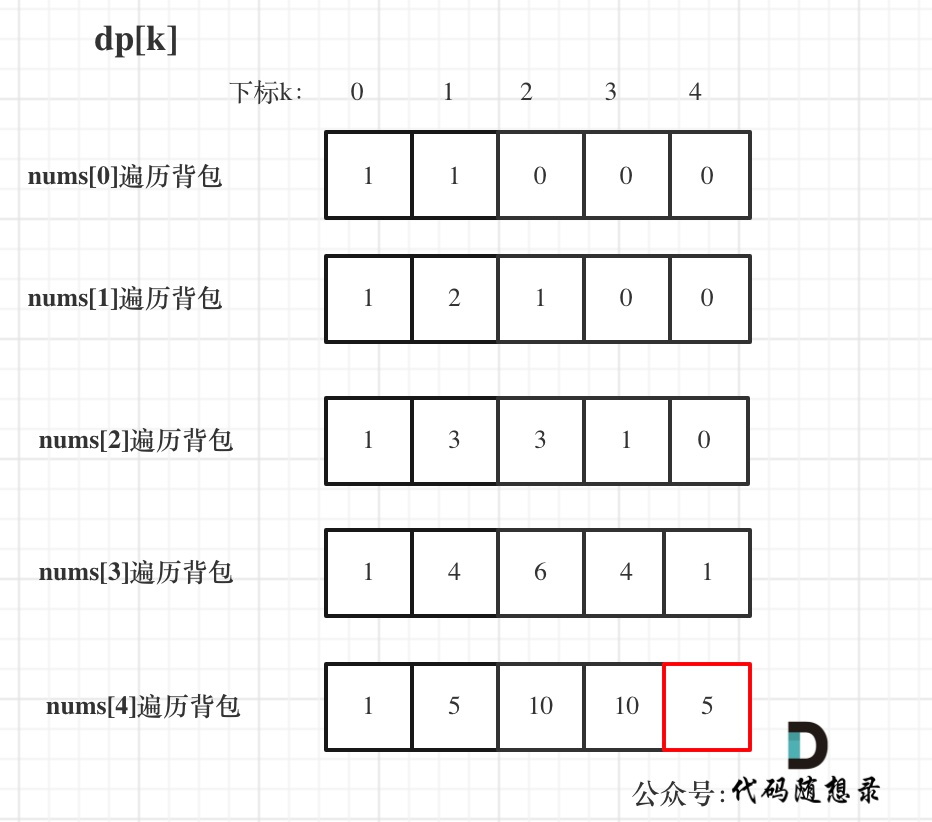

public int findTargetSumWays(int[] nums, int target) {
    int sum = 0;
    for (int i = 0; i < nums.length; i++) {
        sum += nums[i];
    }
    if (Math.abs(target) > sum) return 0;   // 此时绝对值大于sum，已经不满足
    if ((sum + target) % 2 == 1) return 0;  // 例如sum = 5, target = 2，此时就不满足
    int bagSize = (sum + target) / 2;   // 表示最大背包
    // dp[i]表示填满j（包括j）这么大容积的包，有dp[j]种方法
    int[] dp = new int[bagSize + 1];
    dp[0] = 1;  // 凑成总和为0的共有1钟
    for (int i = 0; i < nums.length; i++) {
        for (int j = bagSize; j >= nums[i]; j--) {
            dp[j] += dp[j - nums[i]];
        }
    }
    return dp[bagSize];
}