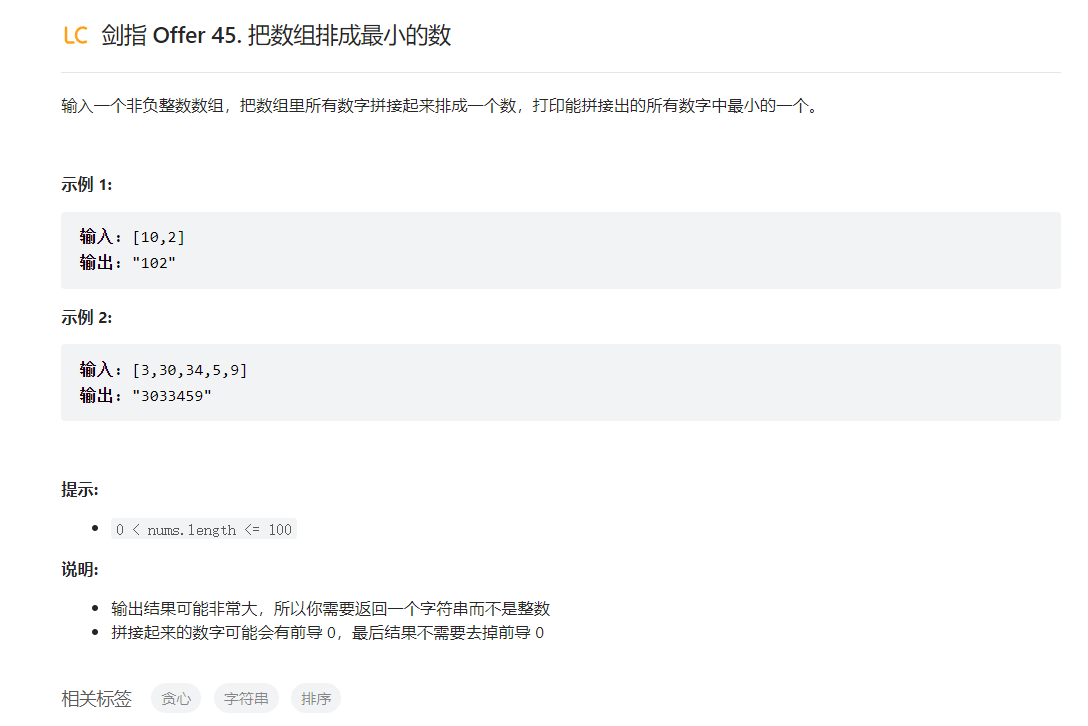
题目描述

解题思路

此题求拼接起来的最小数字，本质上是一个排序问题。设数组 nums 中任意两数字的字符串为 x 和 y ，则规定 排序判断规则 为：

• 若拼接字符串 x + y > y + x ，则 x “大于” y ；
• 反之，若 x + y < y + x ，则 x “小于” y ；

x “小于”y 代表：排序完成后，数组中 x 应在 y 左边；“大于” 则反之。根据以上规则，套用任何排序方法对 nums 执行排序即可。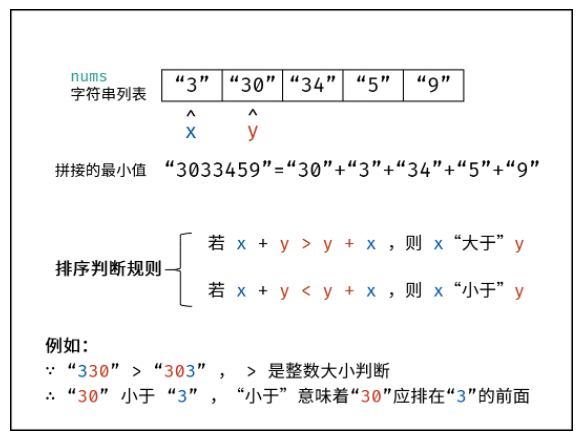

算法流程：

• 初始化： 字符串列表 strs ，保存各数字的字符串格式；
• 列表排序： 应用以上 “排序判断规则” ，对 strs 执行排序；
• 返回值： 拼接 strs 中的所有字符串，并返回。

复杂度分析：

• 时间复杂度 O(NlogN) ： NN 为最终返回值的字符数量（ strs列表的长度 ≤N ）；使用快排或内置函数的平均时间复杂度为 O(NlogN) ，最差为 O(N^2)) 。
• 空间复杂度 O(N) ： 字符串列表 strs 占用线性大小的额外空间。

本题重要的思路为，自定义排序策略，从而符合题目要求谁在前面，谁在后面。

class Solution {
    public String minNumber(int[] nums) {
        String[] array = new String[nums.length];
        for (int i = 0; i < nums.length; i++) {
            array[i] = String.valueOf(nums[i]);
        }
        quickSort(array, 0, array.length - 1);
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < array.length; i++) {
            sb.append(array[i]);
        }
        return sb.toString();
    }
    public void quickSort(String[] array, int l, int r) {
        if (l >= r) {
            return;
        }
        int i = l, j = r;
        while (i < j) {
            while (i < j && (array[j] + array[l]).compareTo(array[l] + array[j]) >= 0) j--;
            while (i < j && (array[i] + array[l]).compareTo(array[l] + array[i]) <= 0) i++;
            swap(array, i, j);
        }
        swap(array, l, i);
        quickSort(array, l, i - 1);
        quickSort(array, i + 1, r);
    }
    public void swap(String[] array, int i, int j) {
        String temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }
}