14. 无重叠区间（435）

一、题目内容 中等

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。
示例1

输入: intervals = [[1,2],[2,3],[3,4],[1,3]] 输出: 1 解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例2：

输入: intervals = [ [1,2], [1,2], [1,2] ] 输出: 2 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例3：

输入: intervals = [ [1,2], [2,3] ] 输出: 0 解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

提示：

• 1 <= intervals.length <= 105
• intervals[i].length == 2
• -5 * 104 <= starti < endi <= 5 * 104

  二、解题思路

  看着这道题，我们先想到的就是排序，排序完了，再去比较区间。
  先来想想排序，按照左边界排序，还是按照右边界排序。
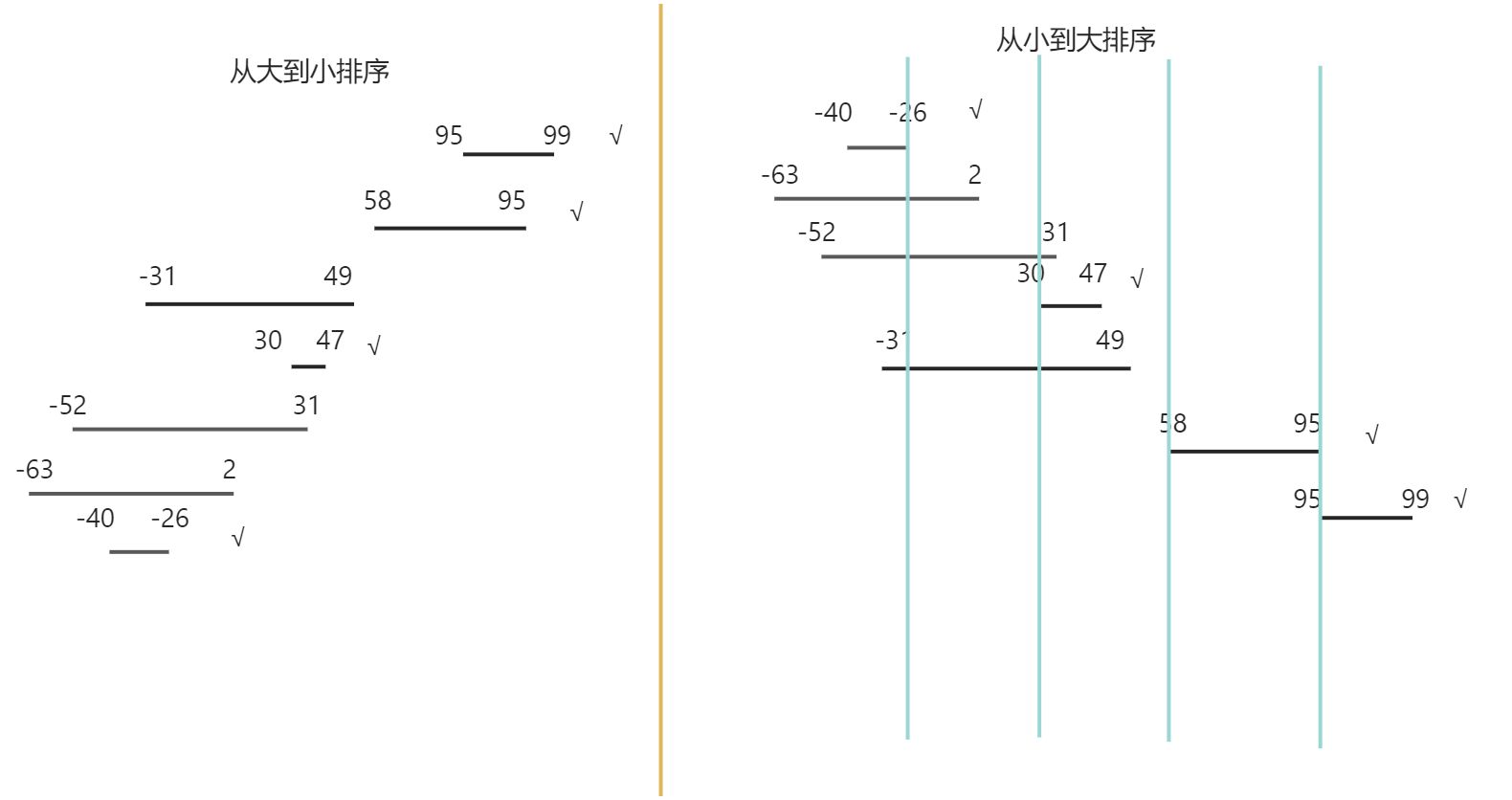
  我们举个例子：[[-52,31],[-31,49],[-62,-49],[95,99],[58,95],[-63,2],[30,47],[-40,-26]]

1. 按照左边界排序
   1. 如果是从小到大排序，你会发现，解不出题。既没法算出不重叠区间个数，也没法算出重叠区间个数
   2. 如果是从大到小排序，然后你把 let [left, right] = intervals[i]的 i 的 left 和 i + 1 的 right 比较，找出不重叠区间个数。然后重叠区间的个数就等于 总数 - 不重叠个数。

1. 按照右边界排序
   1. 如果是从大到小排序，你会发现，解不出题。既没法算出不重叠区间个数，也没法算出重叠区间个数
   2. 如果是从小到大排序，然后你把 let [left, right] = intervals[i]的 i 的 right 和 i + 1 的 left 比较，找出不重叠区间个数。然后重叠区间的个数就等于 总数 - 不重叠个数。

三、具体代码

/**
 * @param {number[][]} intervals
 * @return {number}
 */
var eraseOverlapIntervals = function (intervals) {
  if (intervals.length < 2) return 0
  intervals.sort((a, b) => b[0] - a[0]) // 左边界，从大到小排序
  let count = 1
  let end = intervals[0][0] // 左边界
  for (let i = 1, len = intervals.length; i < len; i++) {
    if (end >= intervals[i][1]) {
      count++
      end = intervals[i][0]
    }
  }
  return intervals.length - count
};

/**
 * @param {number[][]} intervals
 * @return {number}
 */
var eraseOverlapIntervals = function (intervals) {
  if (intervals.length < 2) return 0
  intervals.sort((a, b) => a[1] - b[1]) // 右边界，从小到大排序
  let count = 1
  let end = intervals[0][1]
  for (let i = 1, len = intervals.length; i < len; i++) {
    if (intervals[i][0] >= end) { 
      count++
      end = intervals[i][1]
    }
  }
  return intervals.length - count
};

四、其他解法