一、二叉树的种类

在我们解题过程中二叉树有两种主要的形式：满二叉树和完全二叉树。

1. 满二叉树

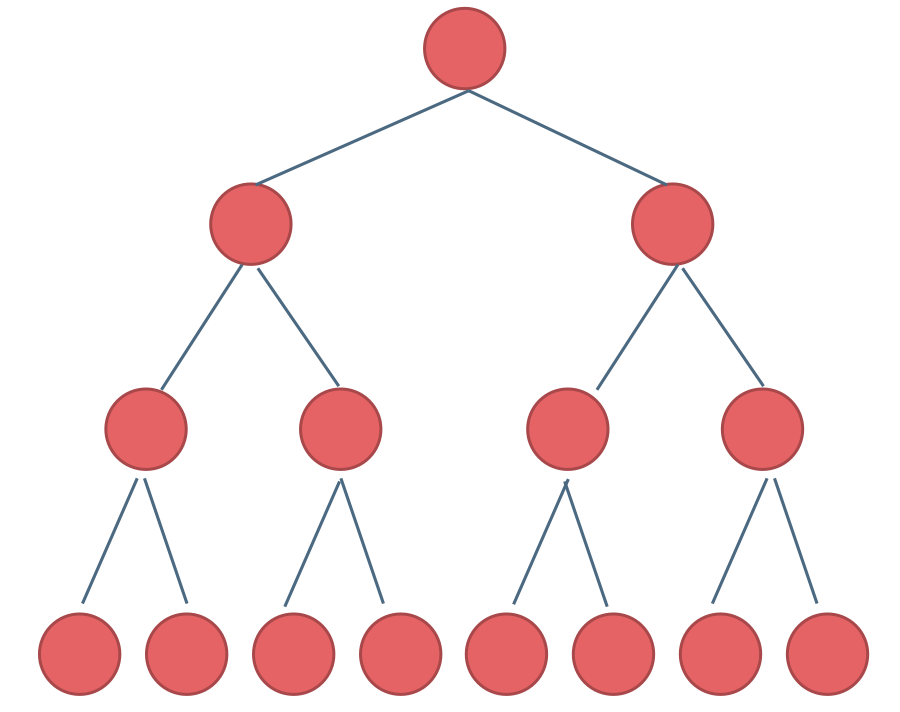
满二叉树：如果一棵二叉树只有度为 0 的结点和度为 2 的结点，并且度为 0 的结点在同一层上，则这棵二叉树为满二叉树。
如图所示

这棵二叉树为满二叉树，也可以说深度为 k，有个节点的二叉树。

2. 完全二叉树

完全二叉树的定义如下：
在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^h -1 个节点。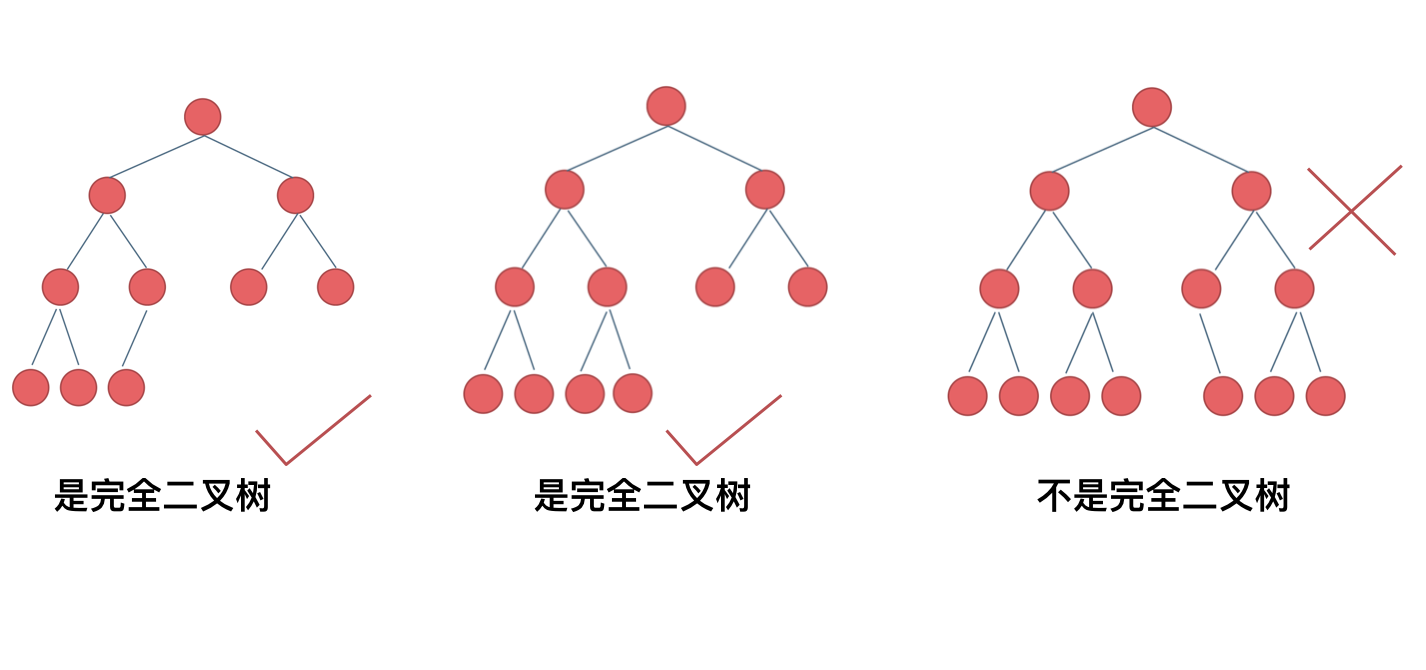

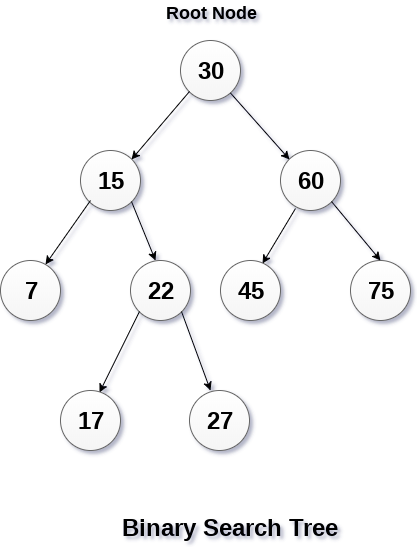
3. 二叉搜索树

二叉查找树又叫二叉搜索树。 二叉搜索树

• 查找时间复杂度为 O(log2N) —— 很好理解，相当于二分搜索

二叉搜索树具有以下性质：

1. 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 它的左、右子树也分别为二叉搜索树。

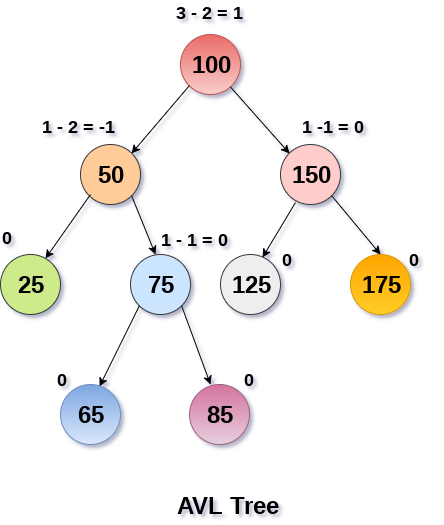
4. 平衡二叉树（AVL Tree）

AVL 树全称 G.M. Adelson-Velsky 和 E.M. Landis，这是两个人的人名。

AVL 树本质上还是一棵二叉搜索树，它的特点是：

1. 本身首先是一棵二叉搜索树。
2. 每个节点的左右子树的高度之差的绝对值（平衡因子）最多为 1。

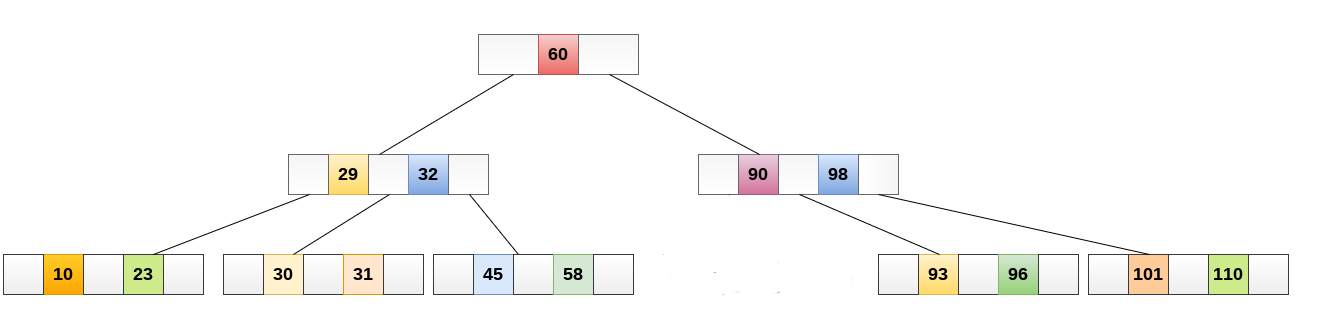
5. B 树

一个 m 阶的 B 树是一个有以下属性的树

1. 每一个节点最多有 m 个子节点
2. 每一个非叶子节点（除根节点）最少有 ⌈m/2⌉ 个子节点，⌈m/2⌉表示向上取整。
3. 如果根节点不是叶子节点，那么它至少有两个子节点
4. 有 k 个子节点的非叶子节点拥有 k − 1 个键
5. 所有的叶子节点都在同一层

6. B+ 树

B+树是从 B 树衍生而来。
跟 B 的不同：
1、B+ 树非叶子节点不存放数据，只存放 keys。
2、B+ 树的叶子节点之间存在指针相连，而且是单链表。

现代操作系统中，磁盘的存储结构使用的是 B+ 树机制，mysql 的 innodb 引擎的存储方式也是 B+ 树机制

二、二叉树的存储

二叉树可以链式存储，也可以顺序存储。
那么链式存储方式就用指针， 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在散落在各个地址的节点串联一起。

1. 链式存储

// JS 定义树节点
function TreeNode(val, left, right) {
    this.val = (val === undefined ? 0 : val)
    this.left = (left === undefined ? null : left)
    this.right = (right === undefined ? null : right)
}

2. 顺序存储

链式存储是大家很熟悉的一种方式，那么我们来看看如何顺序存储呢？
其实就是用数组来存储二叉树，顺序存储的方式如图：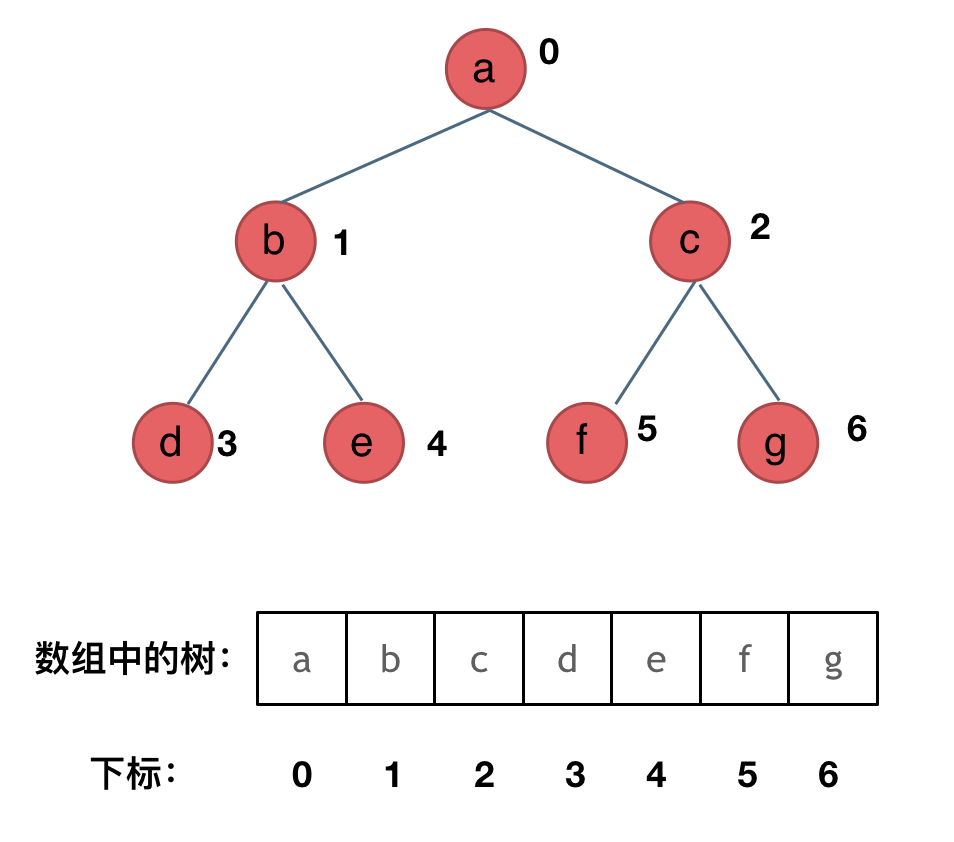

用数组来存储二叉树如何遍历的呢？
如果父节点的数组下标是 i，那么它的左孩子就是 i 2 + 1，右孩子就是 i 2 + 2。
但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。
所以大家要了解，用数组依然可以表示二叉树。

三、二叉树的遍历方式

二叉树主要有两种遍历方式：

1. 深度优先遍历：先往深走，遇到叶子节点再往回走。
   1. 前序遍历（递归法，迭代法）
   2. 中序遍历（递归法，迭代法）
   3. 后序遍历（递归法，迭代法）
2. 广度优先遍历：一层一层的去遍历
   1. 层次遍历（迭代法）

深度优先遍历 DFS

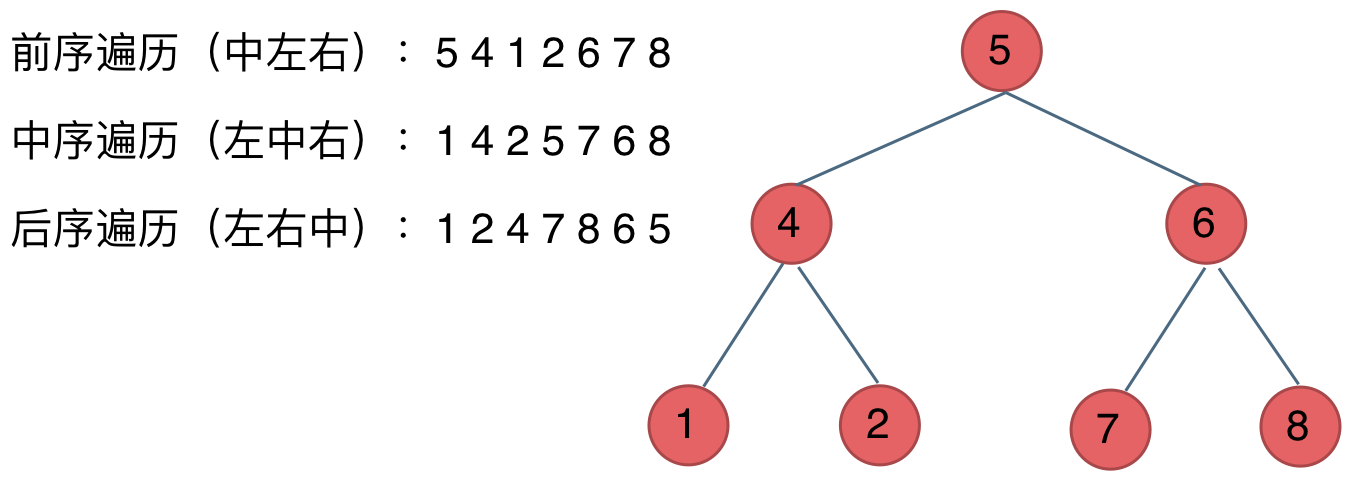
看如下中间节点的顺序，就可以发现，中间节点的顺序就是所谓的遍历方式

• 前序遍历：中左右
• 中序遍历：左中右
• 后序遍历：左右中

// 先序遍历
const preOrder = (root) => {
  if (!root) return;
    console.log(root.val);
  preOrder(root.left);
  preOrder(root.right);
}
// 中序遍历
const inOrder = (root) => {
  if (!root) return;
  preOrder(root.left);
  console.log(root.val);
  preOrder(root.right);
}
// 后序遍历
const postOrder = (root) => {
  if (!root) return;
  preOrder(root.left);
  preOrder(root.right);
  console.log(root.val);
}

广度有限遍历 BFS

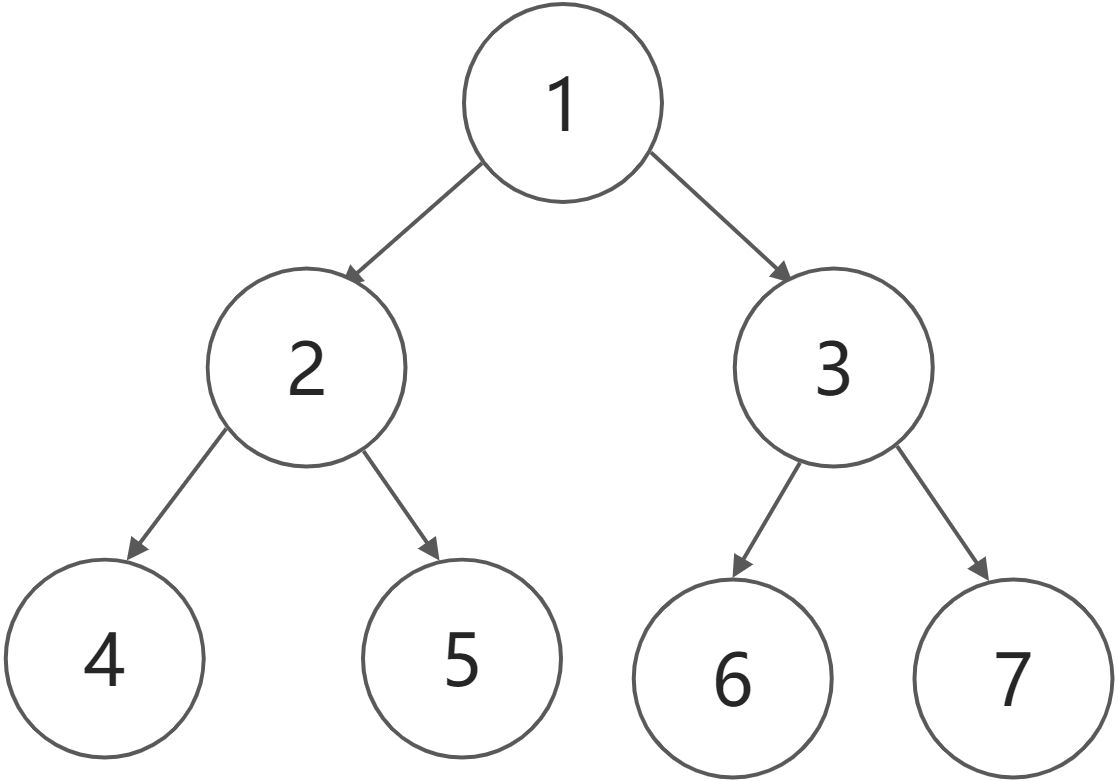
const bfs = (root) => {
    const queue = [root];
  while(queue.length) {
      const node = queue.shift();
    console.log(node.val); // 这一行的 console 代表，对该节点的任意操作
    node.left && queue.push(node.left);
    node.right && queue.push(node.right);
  }
}