21. 删除二叉搜索树中的节点（450）

一、题目内容 中等

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

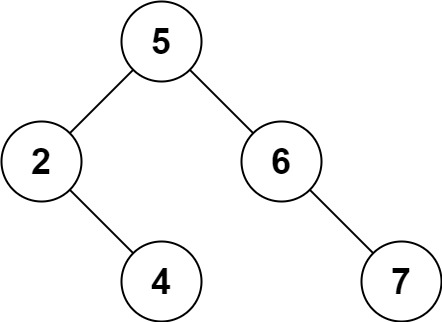
示例1：

输入：root = [5,3,6,2,4,null,7]， key = 3 输出：[5,4,6,2,null,null,7] 解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]

示例2：

输入: root = [5,3,6,2,4,null,7], key = 0 输出: [5,3,6,2,4,null,7] 解释: 二叉树不包含值为 0 的节点

示例3：

输入: root = [], key = 0 输出: []

提示:

• 节点数的范围 [0, 104].
• -105 <= Node.val <= 105
• 节点值唯一
• root 是合法的二叉搜索树
• -105 <= key <= 105

二、解题思路

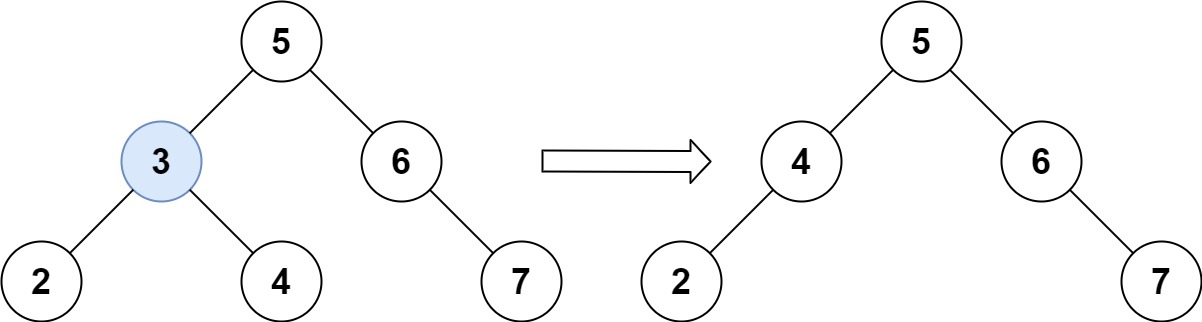
看图说话，要先找到 3。

1. 从 5 开始，3 < 5，往左子树走
2. 走到 3，相等。由于 3 的右子树肯定都大于 3，也就都大于 3 的左子树
   1. 所以，把 3 的左子树都放到右子树的最底层左子树
   2. 然后用 3 的右子树代替节点 3，作为 5 的左子树

三、具体代码

const insertLeft = (root, left) => {
  while (root.left) root = root.left
  root.left = left
}
/**
 * @param {TreeNode} root
 * @param {number} key
 * @return {TreeNode}
 */
var deleteNode = function (root, key) {
  if (!root) return null
  if (root.val < key) root.right = deleteNode(root.right, key)
  else if (root.val > key) root.left = deleteNode(root.left, key)
  else {
    const left = root.left
    const right = root.right
    if (right) {
      insertLeft(right, left)
      return right
    }
    return left
  }
  return root
};

四、其他解法

const insertLeft = (root, left) => {
  while (root.left) root = root.left
  root.left = left
}
/**
 * @param {TreeNode} root
 * @param {number} key
 * @return {TreeNode}
 */
var deleteNode = function (root, key) {
  if (!root) return null
  const queue = [root]
  let p = null // 记录 node 的父节点
  while (queue.length) {
    const node = queue.shift()
    if (node.val < key) {
      if (node.right) queue.push(node.right)
    } else if (node.val > key) {
      if (node.left) queue.push(node.left)
    } else {
      let left = node.left
      let right = node.right
      // 将左子树放到右子树的最底层左子树
      if (right) insertLeft(right, left)
      else right = left
      // 删除节点
      if (!p) return right
      if (!right) {
        if (p.val > key) p.left = null
        else p.right = null
      } else {
        if (p.val > right.val) p.left = right
        else p.right = right
      }
    }
    p = node
  }
  return root
};