5. 二叉树的最小深度（111）

一、题目内容 简单

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。

示例1：

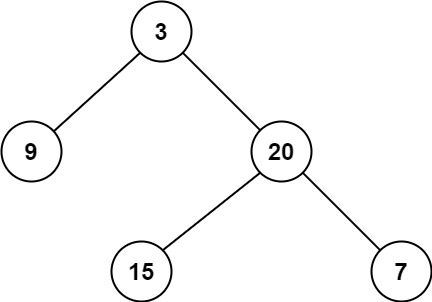
输入：root = [3,9,20,null,null,15,7] 输出：2

示例2：

输入：root = [2,null,3,null,4,null,5,null,6] 输出：5

提示：

• 树中节点数的范围在 [0, 105] 内

• -1000 <= Node.val <= 1000

  二、解题思路

  
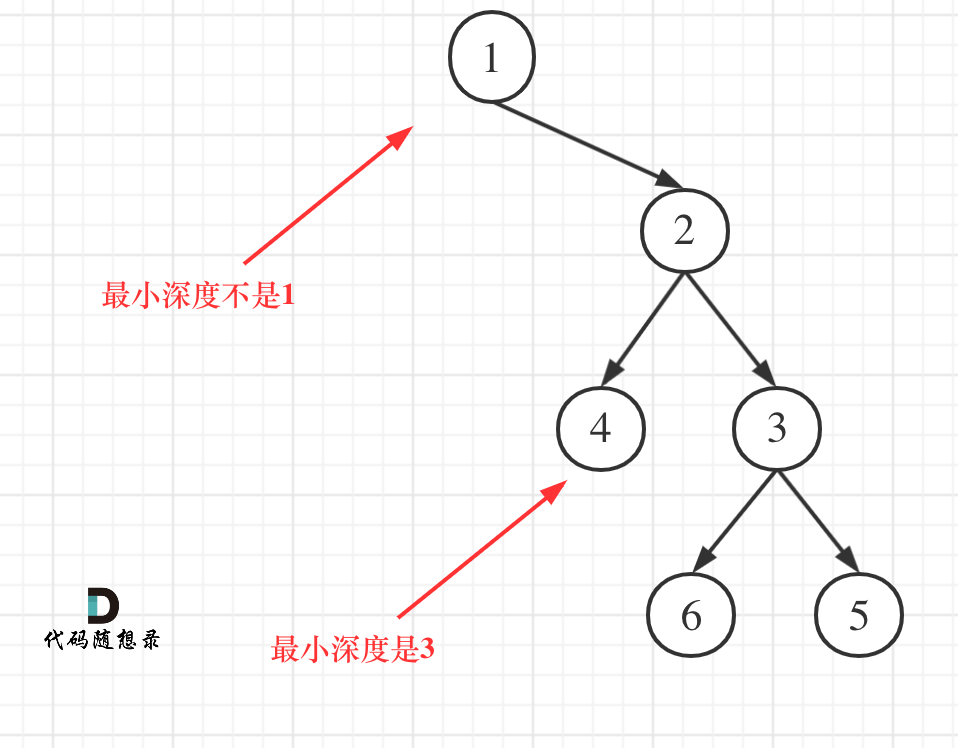
  最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点。
  假设 M 节点的左右子节点为 A，B。
  当 A，B 都不存在时，M 节点的最小深度是 1
  当 A，B 只有一个存在时，选择存在的节点的深度，不存在的深度是 0，存在的深度肯定大
  当 A，B 都存在时，选择两个节点中最小的深度。

  三、具体代码

  /**
  * @param {TreeNode} root
  * @return {number}
  */
  var minDepth = function (root) {
  if (!root) return 0;
  const dfs = (node) => {
    if (!node) return 0
    const leftDeep = dfs(node.left)
    const rightDeep = dfs(node.right)
    if (leftDeep > 0 && rightDeep > 0) return Math.min(leftDeep, rightDeep) + 1
    if (leftDeep > 0 || rightDeep > 0) return Math.max(leftDeep, rightDeep) + 1
    return 1
  }
  return dfs(root)
  };

  四、其他解法

  迭代法

  /**
  * @param {TreeNode} root
  * @return {number}
  */
  var minDepth = function (root) {
  if (!root) return 0
  const queue = [root]
  let minDeep = 0
  while (queue.length) {
    const len = queue.length // 记录下这一层的节点数
    minDeep++ // 进入下一层，就加 1
    // 把这一层的节点 的 左右子节点都放入队列。同时移除这一层的节点
    for (let i = 0; i < len; i++) {
      const node = queue.shift()
      if (node.left) queue.push(node.left)
      if (node.right) queue.push(node.right)
      if (!node.left && !node.right) return minDeep // 如果左右子节点都不存在，说明该节点就是最小深度这一层的节点
    }
  }
  return minDeep
  };