15. 验证二叉搜索树（98）

一、题目内容 中等

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例1：

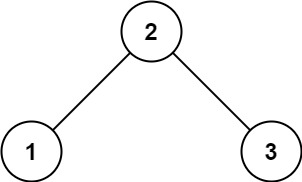
输入：root = [2,1,3] 输出：true

示例2：

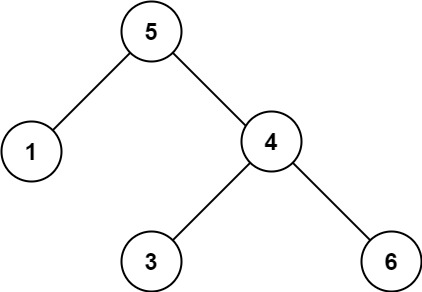
输入：root = [5,1,4,null,null,3,6] 输出：false 解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内

• -231 <= Node.val <= 231 - 1

  二、解题思路

  这个题目有个陷阱：不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了。
  我们要比较的是 左子树所有节点小于中间节点，右子树所有节点大于中间节点。
  例如下面这棵树：6 < 10，不符合要求，不是二叉搜索树。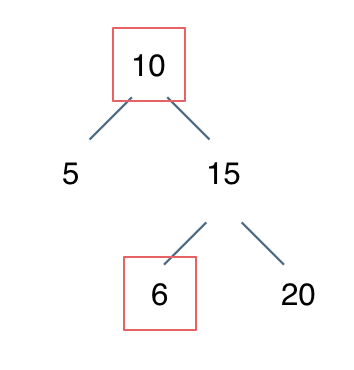
  
  我们来想一想递归可以怎么做，以上面的树为例。
  走到 5 时，是 10 的左节点，小于 10 可以。

• 节点没有子节点，返回 true

• 但是我们假设 5 有子节点来看看情况。5 有左子节点 4，右子节点 6
  • 左子节点 4，需要小于 5，需要小于 10（两个上界，或者说下界无穷小）
  • 右子节点 6，需要大于 5，需要小于 10（下界、上界）

走到 15 时，是 10 的右节点，大于 10 可以。

• 往 15 的左子树走，6 需要小于 15，但需要大于 10（上界、下界）
• 往 15 的右子树走，20 需要大于 15，需要大于 10。（两个下界，或者说上界无穷小）

那么按照这个思路，我们其实遍历每一个节点时，每个节点都是有自己需要满足的上下界。
我们在递归的时候，去改变上下界就好了。那么初始化的时候呢，根节点的上下界是谁？
就试试无穷小、无穷大呗。

const helper = (node, low, high) => {
  if (!node) return true
  if (node.val <= low || node.val >= high) return false
  return helper(node.left, low, node.val) && helper(node.right, node.val, high)
}

三、具体代码

const helper = (node, low, high) => {
  if (!node) return true
  if (node.val <= low || node.val >= high) return false
  return helper(node.left, low, node.val) && helper(node.right, node.val, high)
}
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
  return helper(root, -Infinity, Infinity)
};

/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
  const nums = []
  // 利用二叉搜索树的性质，中序遍历建造有序数组
  // 通过判断数组是否有序，来判断是不是二叉搜索树
  const traversal = (node) => {
    if (!node) return
    traversal(node.left)
    nums.push(node.val)
    traversal(node.right)
  }
  traversal(root)
  if (nums.length < 2) return true
  for (let i = 1, len = nums.length; i < len; i++) {
    if (nums[i] - nums[i - 1] <= 0) return false
  }
  return true
};

四、其他解法

迭代法

这个还真不好想出这么优雅的写法。

/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
  const stack = []
  let pre = null, cur = root
  // 采用中序遍历的方式，先把左节点都压入栈，再抽出 A 节点与 A 节点的左节点比较。
  // 把中间节点压入栈，再把中间节点与其右节点进行比较
  while (cur || stack.length) {
    if (cur) {
      stack.push(cur)
      cur = cur.left        // 记录下左子节点
    } else {
      cur = stack.pop() // 拿出中间节点
      if (pre && pre.val >= cur.val) return false
      pre = cur
      cur = cur.right        // 换到中间节点的右子节点
    }
  }
  return true
};