5. 组合总和II（40）

一、题目内容 中等

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

示例1：

输入: candidates = [10,1,2,7,6,1,5]， target = 8, 输出:[[1,1,6],[1,2,5],[1,7],[2,6]]

示例2：

输入: candidates = [2,5,2,1,2], target = 5, 输出: [ [1,2,2], [5] ]

提示:

• 1 <= candidates.length <= 100
• 1 <= candidates[i] <= 50
• 1 <= target <= 30

二、解题思路

本题的难点在于区别2中：集合（数组candidates）有重复元素，但还不能有重复的组合。
所谓去重，其实就是使用过的元素不能重复选取。 这么一说好像很简单？
组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。
回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。
所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

强调一下，树层去重的话，需要对数组排序！

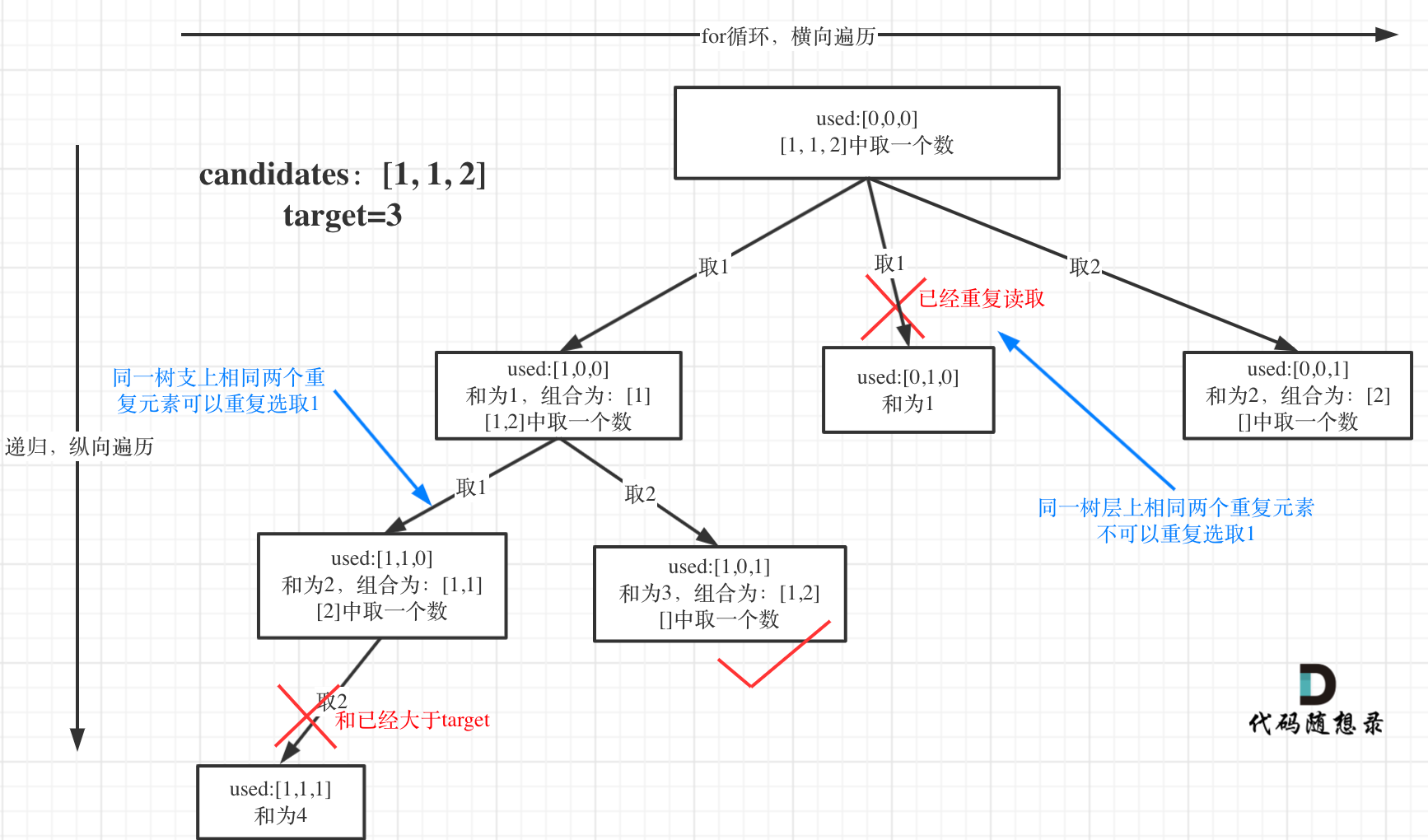
此题需要加一个 bool 型数组 used，用来记录同一树枝上的元素是否使用过。
这个集合去重的重任就是 used 来完成的。

三、具体代码

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum2 = function (candidates, target) {
  candidates.sort((a, b) => a - b) // 对数组进行排序，后续才能在同一层级去重用过的数字
  const result = []
  const path = []
  const used = [] // 用于判断某个数字，是否在同一层级被使用过
  const backTracking = (start, sum) => {
    if (sum > target) return
    if (sum === target) {
      result.push(path.map(i => i))
      return
    }
    for (let i = start; i < candidates.length; i++) {
      // used[i - 1] = true 说明同一树枝使用过
      // used[i - 1] = false 说明同一树层使用过
      if (!used[i - 1] && candidates[i] === candidates[i - 1]) continue
      used[i] = true
      path.push(candidates[i])
      backTracking(i + 1, sum + candidates[i])
      path.pop()
      used[i] = false
    }
  }
  backTracking(0, 0)
  return result
};

四、其他解法