一、题目内容 简单

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩 i ，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j ，都有一个尺寸s[j]
如果s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例1：

输入: g = [1,2,3], s = [1,1] 输出: 1 解释: 你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。 虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。 所以你应该输出1。

示例2：

输入: g = [1,2], s = [1,2,3] 输出: 2 解释: 你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。 你拥有的饼干数量和尺寸都足以让所有孩子满足。 所以你应该输出2.

提示：

  • 1 <= g.length <= 3 * 104
  • 0 <= s.length <= 3 * 104
  • 1 <= g[i], s[j] <= 231 - 1

    二、解题思路

    为了了满足更多的小孩，就不要造成饼干尺寸的浪费。
    大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子，那么就应该优先满足胃口大的。
    这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。
    可以尝试使用贪心策略，先将饼干数组和小孩数组从小到大排序。
    然后从后往前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量。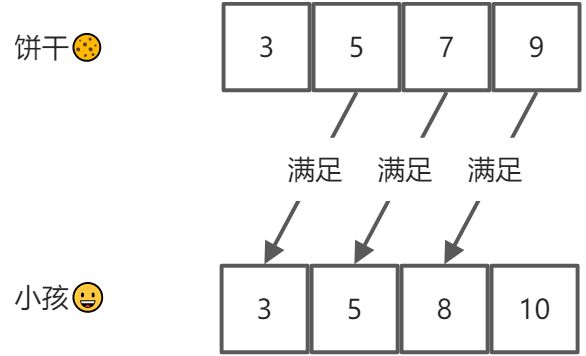
    1. 分发饼干（455） - 图1

    三、具体代码

    1. /**
    2. * @param {number[]} g
    3. * @param {number[]} s
    4. * @return {number}
    5. */
    6. var findContentChildren = function (g, s) {
    7. g.sort((a, b) => a - b)
    8. s.sort((a, b) => a - b)
    9. let j = s.length - 1;
    10. for (let i = g.length - 1; i >= 0; i--) {
    11.   if (s[j] && s[j] >= g[i]) j--
    12. }
    13. return s.length - 1 - j;
    14. };
    15. /**
    16. * 时间复杂度：O(n)
    17. * 空间复杂度：O(1)
    18. */

    四、其他解法