8. 二叉树的所有路径（257）

一、题目内容 简单

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。

示例1：

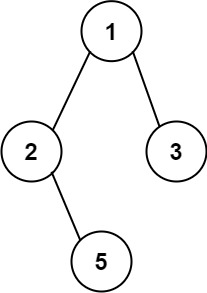
输入：root = [1,2,3,null,5] 输出：["1->2->5","1->3"]

示例2：

输入：root = [1] 输出：[“1”]

提示：

• 树中节点的数目在范围 [1, 100] 内
• -100 <= Node.val <= 100

  二、解题思路

  这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。
  前序遍历以及回溯的过程如图：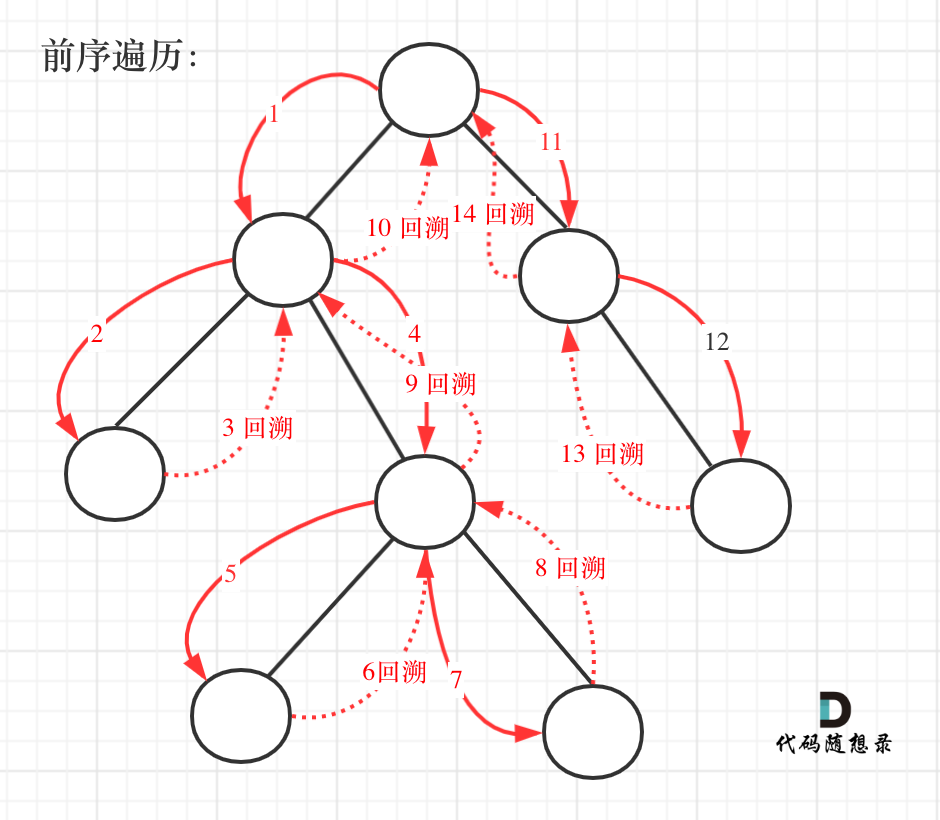

三、具体代码

/**
 * @param {TreeNode} root
 * @return {string[]}
 */
var binaryTreePaths = function (root) {
  const path = []
  const result = []
  const backTracking = (node) => {
    if (!node) return
    path.push(node.val)
    if (!node.left && !node.right) {
      result.push(path.join('->'))
      return
    }
    if (node.left) {
      backTracking(node.left)
      path.pop()
    }
    if (node.right) {
      backTracking(node.right)
      path.pop()
    }
  }
  backTracking(root)
  return result
};

四、其他解法

迭代法

我们可以依然可以使用前序遍历的迭代方式来模拟遍历路径的过程。
遍历过程中的注意事项：

1. 先判断 node.right，再判断 node.left，这样方便做前序遍历
2. paths 和 stack 的顺序保持一致。

var binaryTreePaths = function (root) {
  const stack = [root]
  while (stack.length) {
    // 先从右节点开始，才能方便的前序遍历
    if (node.right) {
      stack.push(node.right)
    }
    if (node.left) {
      stack.push(node.left)
    }
  }
  return result
};

完整代码如下：

/**
 * @param {TreeNode} root
 * @return {string[]}
 */
var binaryTreePaths = function (root) {
  const result = []
  if (!root) return result
  const stack = [root]
  const paths = [root.val]
  while (stack.length) {
    const node = stack.pop()
    const path = paths.pop()
    if (!node.left && !node.right) {
      const tmp = typeof path === 'string' ? path : '' + path
      result.push(tmp)
    }
    // 先从右节点开始，才能方便的前序遍历
    if (node.right) {
      stack.push(node.right)
      paths.push(path + '->' + node.right.val)
    }
    if (node.left) {
      stack.push(node.left)
      paths.push(path + '->' + node.left.val)
    }
  }
  return result
};