力扣题目链接

一、题目内容 中等

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例1：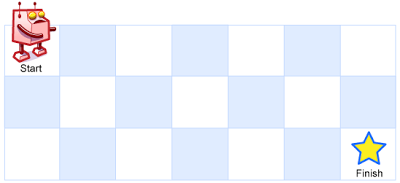
2. 不同路径（62） - 图1

输入：m = 3, n = 7 输出：28

示例2：

输入：m = 3, n = 2 输出：3 解释： 从左上角开始，总共有 3 条路径可以到达右下角。

  1. 向右 -> 向下 -> 向下
  2. 向下 -> 向下 -> 向右
  3. 向下 -> 向右 -> 向下

示例3：

输入：m = 7, n = 3 输出：28

示例4：

输入：m = 3, n = 3 输出：6

二、解题思路

先假设，m = 1，n = 1 的时候，这时有一条路，n 不断增大，还是一条路。
同理，n = 1 时，m 不断增大，还是一条路。

这会是我们后面的初始条件

假设，m = 2，n = 2 的情况，这时有 2 条路
我们把走到的那个格子，上面表上数字，表示走到这个格子，可以有几条路（左上角为原点）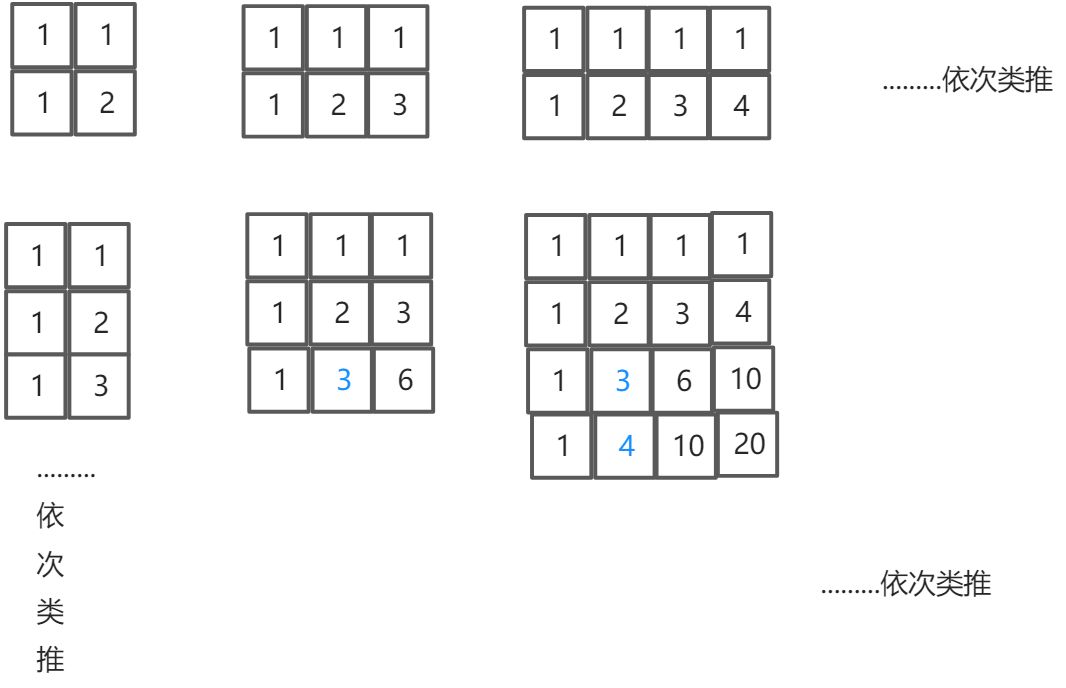
2. 不同路径（62） - 图2

于是，我们可以的得出结论：除了第一行、第一列的格子，其他格子的数 等于 它的上面格子 + 它的左边格子

由于机器人只能往右走、往下走 那么每个格子的道路的数，也就等于 它能从左边来的道路数 + 从上面来的道路数

  1. 我们用 dp 表示格子数组，m 表示对应第几行，n 表示对应第几列
  2. 所以由此写出递推公式： dp[m][n] = dp[m - 1][n] + dp[m][n - 1]
  3. 而我们的初始化：dp[0][n] = 1 dp[n][0] = 1

动规三部曲有了，接下来写代码

三、具体代码

  1. /**
  2.  * @param {number} m
  3.  * @param {number} n
  4.  * @return {number}
  5.  */
  6. var uniquePaths = function (m, n) {
  7.   // 构造一个 m x n 的数组 dp
  8.   // 初始化 dp[0][n] = 1，dp[n][0] = 1
  9.   // 递推公式：dp[m][n] = dp[m-1][n] + dp[m][n-1]
  10.   const dp = new Array(m).fill(1).map(() => new Array(n).fill(1));
  11.   for (let i = 1; i < m; i++) {
  12.     for (let j = 1; j < n; j++) {
  13.       dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
  14.     }
  15.   }
  16.   return dp[m - 1][n - 1]
  17. };
  18. /**
  19.  * 时间复杂度：O(m x n x 2)
  20.  * 空间复杂度: O(m x n)
  21.  */

四、其他解法