• 一种分层数据的抽象模型
• 前端工作中常见的树包括：DOM树、级联选择、树形控件
• JS没有树，但可以用Object和Array构建树
• 树的常见操作：深度/广度优先遍历、先中后序遍历

深度/广度遍历

深度优先遍历

• 概念：尽可能深的搜索树的分支

• 深度优先遍历的 算法口诀

  • 访问根节点
  • 对根节点的children 挨个进行深度优先遍历

    广度优先遍历

• 概念：先访问离根节点最近的节点

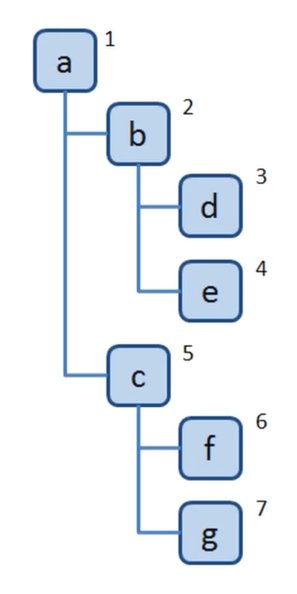
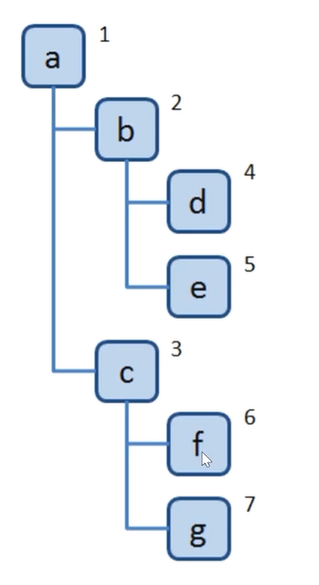
• 广度优先遍历的 算法口诀
  • 1.新建一个队列，把根节点入队
  • 2.把队头出队，并访问
  • 3.把对头的children挨个入队
  • 4.重复第二、第三步，直到队列为空

二叉树

• 二叉树：树中每个节点最多只能由两个子节点
  • 在JS中，常用Object来模拟二叉树

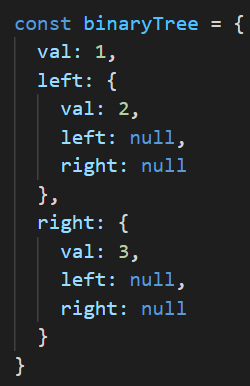
const bt = {
  val: 1,
  left: {
    val: 2,
    left: {
      val: 4,
      left: null,
      right: null,
    },
    right: {
      val: 5,
      left: null,
      right: null,
    }
  },
  right: {
    val: 3,
    left: {
      val: 6,
      left: null,
      right: null
    },
    right: {
      val: 7,
      left: null,
      right: null
    }
  }
}
module.exports = bt;

先序遍历

递归版

• 先序遍历的算法口诀
  • 访问根节点
  • 对根节点的左子树进行先序遍历
  • 对根节点的右子树进行先序遍历

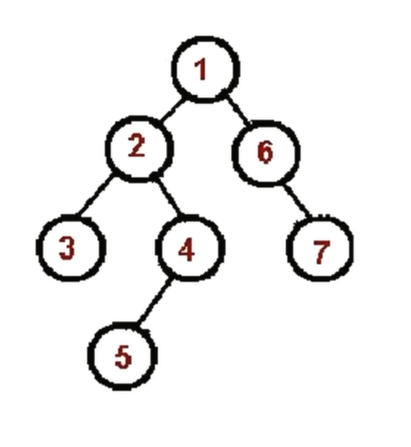
• 对这个树：1—>2—>3—>4—>5—>6—>7

  const preOrder = (root) => {
  if(!root) return;
  console.log(root.val);
  preOrder(root.left);
  preOrder(root.right);
  }

  非递归版

  const preOrder = (root) => {
  if (!root) return;
  const stack = [root]; // 用栈模仿递归的栈
  while (stack.length) {
    const node = stack.pop();
    console.log(node.val);
    if (node.right) stack.push(node.right);
    if (node.left) stack.push(node.left);
  }
  }

  中序遍历

  递归版

• 中序遍历的算法口诀

  • 对根节点的左子树进行中序遍历
  • 访问根节点
  • 对根节点的右子树进行中序遍历

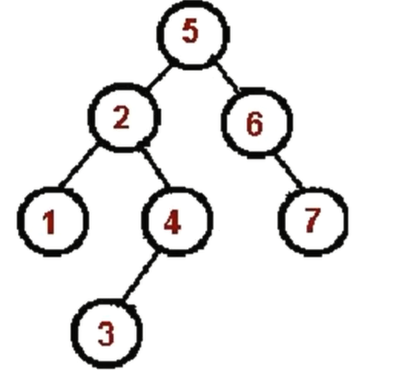
• 对这个树：1—>2—>3—>4—>5—>6—>7

  const inOrder = (root) => {
  if (!root) return;
  inOrder(root.left);
  console.log(root.val);
  inOrder(root.right);
  }

  非递归版

  ```javascript const inOrder = (root) => { if (!root) return; const stack = []; let p = root; // 声明一个指针 while (stack.length || p) { while (p) {

  stack.push(p);
  p = p.left;

  } const node = stack.pop(); console.log(node.val); p = node.right; }

}

<a name="WpzKa"></a>
## 后序遍历
<a name="KbN4Q"></a>
### 递归版
- 后序遍历的算法口诀
   - 对根节点的**左**子树进行后序遍历
   - 对根节点的**右**子树进行后序遍历
   - 访问根节点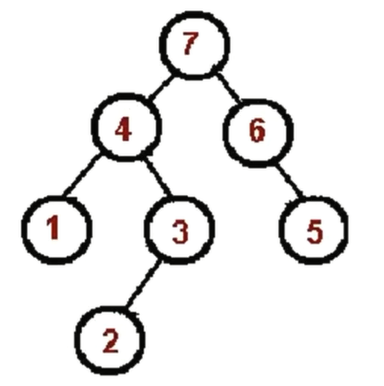
![image.png](https://cdn.nlark.com/yuque/0/2021/png/1174243/1628826838258-11b23a4a-b6ba-43bd-8ad2-ca1124db86c3.png#clientId=uafeef4ad-9357-4&from=paste&height=193&id=u23d611ab&margin=%5Bobject%20Object%5D&name=image.png&originHeight=386&originWidth=384&originalType=binary&ratio=1&size=60448&status=done&style=none&taskId=ub998ee29-5196-4eee-b1f2-88a47dc57dd&width=192)
- 对这个树：1—>2—>3—>4—>5—>6—>7
```javascript
const postOrder = (root) => {
  if(!root) return;
  postOrder(root.left);
  postOrder(root.right);
  console.log(root.val);
}

非递归版

const postOrder = (root) => {
  if (!root) return;
  const stack = [root];
  const outputStack = [];
  while (stack.length) {
    const node = stack.pop();
    outputStack.push(node);
    if (node.left) stack.push(node.left);
    if (node.right) stack.push(node.right);
  }
  while(outputStack.length) {
    const node = outputStack.pop();
    console.log(node.val);
  }
}