一、题目内容 中等

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组[numsl, numsl+1, ..., numsr-1, numsr]，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例1：

输入：target = 7, nums = [2,3,1,2,4,3] 输出：2 解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例2：

输入：target = 4, nums = [1,4,4] 输出：1

示例3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1] 输出：0

提示：

  • 1 <= target <= 109
  • 1 <= nums.length <= 105
  • 1 <= nums[i] <= 105

进阶：

  • 如果你已经实现_ _O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

    二、解题思路

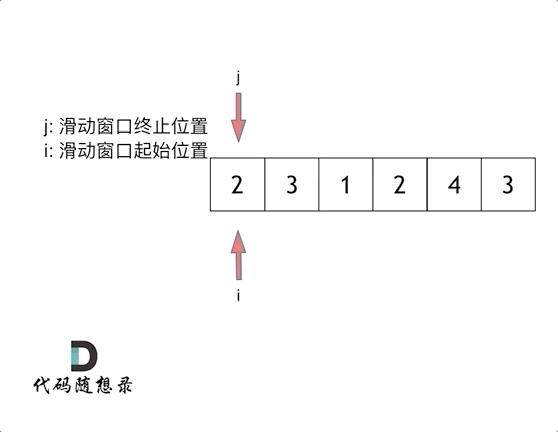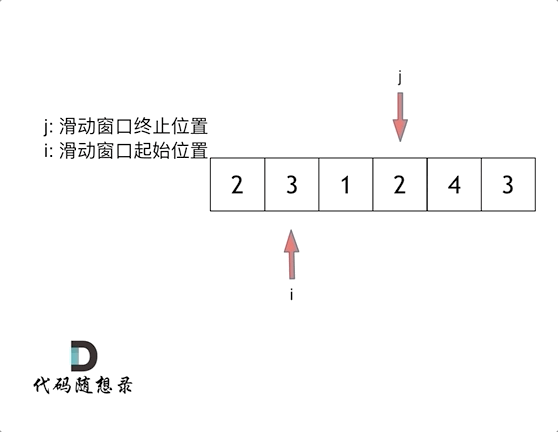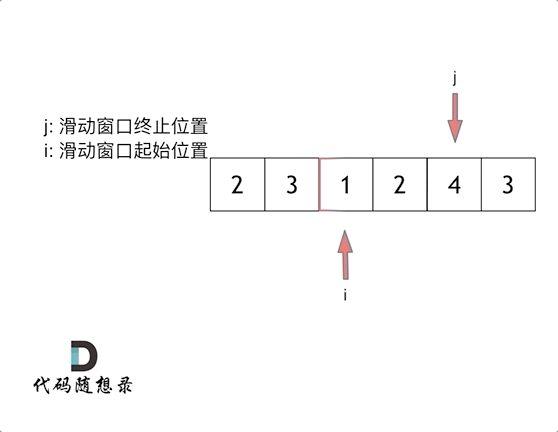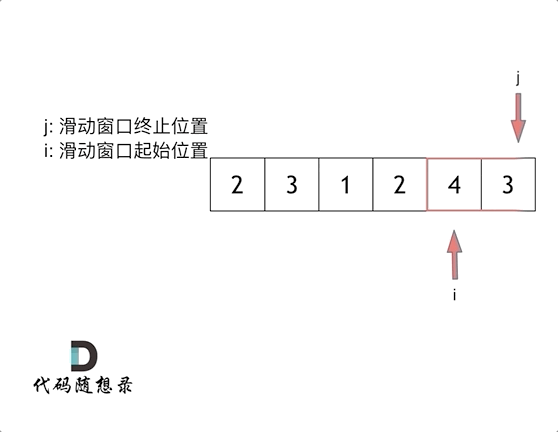
    1. 双指针，做滑动窗口

    由于要找出 连续子数组，那么一个数组找连续，就可以用滑动的窗口，一个指针慢慢向前，一个指针在需要的时候往前，将窗口缩小。
  1. 假设窗口内的总和是 sum，窗口左右指针为 left、right
  2. 我们把将 right 指针先走，sum = nums[right]
  3. 当遇到 sum > target，就考虑将 left 指针往前，缩小窗口，找出最小数组。

4. 长度最小的子数组（209） - 图1

三、具体代码

  1. /**
  2.  * @param {number} target
  3.  * @param {number[]} nums
  4.  * @return {number}
  5.  */
  6. var minSubArrayLen = function (target, nums) {
  7.   let minLen = Infinity
  8.   let sum = 0
  9.   let left = 0
  10.   for (let right = 0; right < nums.length; right++) {
  11.     sum += nums[right]
  12.     if (sum >= target) {
  13.       while (sum >= target) {
  14.         minLen = Math.min(right - left + 1, minLen)
  15.         sum -= nums[left]
  16.         left++
  17.       }
  18.     }
  19.   }
  20.   if (minLen === Infinity) return 0
  21.   return minLen
  22. };
  23. /**
  24.  * 时间复杂度：O(n)
  25.  * 空间复杂度：O(1)
  26.  */

四、其他解法

1. 暴力循环

  1. /**
  2.  * @param {number} target
  3.  * @param {number[]} nums
  4.  * @return {number}
  5.  */
  6. var minSubArrayLen = function (target, nums) {
  7.   let minLen = Infinity
  8.   let sum = 0
  9.   for (let i = 0; i < nums.length; i++) {
  10.     for (let j = i; j < nums.length; j++) {
  11.       sum += nums[j]
  12.       if (sum >= target) minLen = Math.min(j - i + 1, minLen)
  13.     }
  14.     sum = 0
  15.   }
  16.   if (minLen === Infinity) return 0
  17.   return minLen
  18. };
  19. /**
  20.  * 时间复杂度：O(n^2)
  21.  * 空间复杂度：O(1)
  22.  */