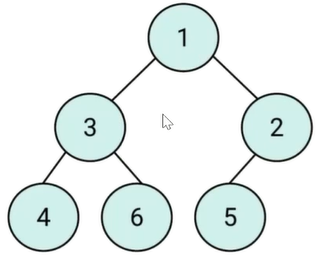
简介
如何创建一个大（小）顶堆
- 插入式建堆
  - 最小堆类的实现
- 原地建堆
  - 自下而上的堆化

简介

堆是一种特殊的完全二叉树
- 完全二叉树：每层节点都完全填满，在最后一层如果不是满的，则只缺少右边的若干节点
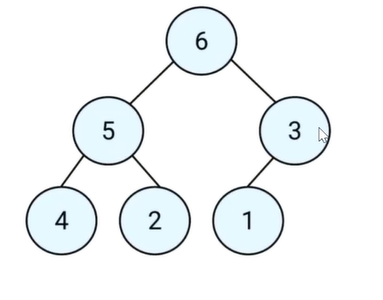
- 满二叉树：特殊的完全二叉树。每一层都是满的

最大堆：所有节点都大于等于其子节点最小堆：所有节点都小于等于其子节点

JS中的堆：数组来表示堆
- 树去广度优先遍历
左侧子节点的位置是2 * index(父节点位置) + 1
右侧子节点的位置是2 * index(父节点位置) + 2
父节点的位置是[index(自己的位置) - 1] / 2，向下取整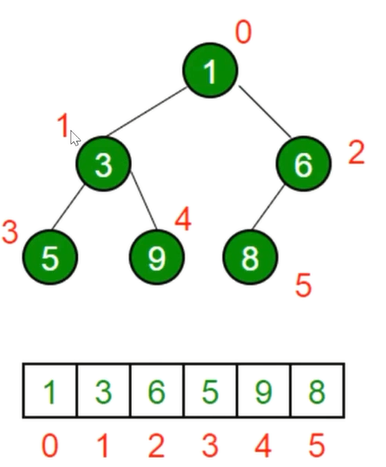

堆的应用
- 堆能高效、快速地找出最大值，最小值
  - 时间复杂度为 O(1)
- 找出第K个最大（小）元素

如何创建一个大（小）顶堆

常用的方式有两种：

插入式创建：每次插入一个节点，实现一个大顶堆（或小顶堆）
原地创建：又称堆化，给定一组节点，实现一个大顶堆（或小顶堆）

插入式建堆

最小堆类的实现
实现步骤
- 在类里，声明一个数组，用来装元素
- 插入
  - 将值插入堆的底部，即数组的尾部
  - 然后上移：将这个值和它的父节点进行交换，直到父节点小于等于这个插入的值
  - 大小为K的堆中，插入元素的时间复杂度为O(logk)
- 删除堆顶
  - 用数组尾部元素替换堆顶(直接删除堆顶会破坏堆结构)
  - 然后下移：将新堆顶和它子节点进行交换，直到子节点大于等于这个新堆顶
  - 大小为k的堆中，删除元素的时间复杂度为O(logk)
- 获取堆顶
  - 返回数组头部
- 获取堆大小
  - 返回数组长度 ```javascript class miniHeap { constructor() { this.heap = []; }
// 获取父节点的位置 getParentIndex(i) { return (i - 1) >> 1; } // 获取左侧子节点 getLeftIndex(i) { return i * 2 + 1; }

// 获取右侧子节点 getRightIndex(i) { return i * 2 + 2; }

swap(i1, i2) { const tmp = this.heap[i1]; this.heap[i1] = this.heap[i2]; this.heap[i2] = tmp; }

// 将节点上移，直到父节点小于等于这个节点 shiftUp(index) { if (index === 0) return; const parentIndex = this.getParentIndex(index); if (this.heap[parentIndex] > this.heap[index]) {
```
this.swap(parentIndex, index);
this.shiftUp(parentIndex);
```
} }

// 将节点进行下移，直到父节点小于等于这个节点 shiftDown(index) { const leftIndex = this.getLeftIndex(index); const rightIndex = this.getRightIndex(index); if (this.heap[leftIndex] < this.heap[index]) {
```
this.swap(leftIndex, index);
this.shiftDown(leftIndex);
```
} if (this.heap[rightIndex] < this.heap[index]) {
```
this.swap(rightIndex, index);
this.shiftDown(rightIndex);
```
} }

pop() { this.heap[0] = this.heap.pop(); this.shiftDown(0); }

insert(value) { this.heap.push(value); this.shiftUp(this.heap.length - 1); } peek() { return this.heap[0]; }

size() { return this.heap.length; } }

const h = new miniHeap();

h.insert(3); h.insert(2); h.insert(1); h.pop();

<a name="TFstA"></a>
### 最大堆类的实现
```javascript
class MaxHeap {
  constructor() {
    this.heap = []
  }
  getParentIndex(index) {
    return index >> 1
  }
  swap(i, j) {
    const tmp = this.heap[i]
    this.heap[i] = this.heap[j];
    this.heap[j] = tmp;
  }
  shiftUp(index) {
    if (index === 0) return;
    const { heap } = this;
    const parentIndex = this.getParentIndex(index);
    if (heap[parentIndex] < heap[index]) {
      this.swap(parentIndex, index);
      this.shiftUp(parentIndex);
    }
  }
  insert(value) {
    this.heap.push(value);
    this.shiftUp(this.heap.length - 1)
  }
  peek() {
    return this.heap[0];
  }
  size() {
    return this.heap.length;
  }
}

原地建堆

原地建堆的方法有两种：

自下而上式堆化 ：将节点与其父节点比较，如果节点大于父节点（大顶堆）或节点小于父节点（小顶堆），则节点与父节点调整位置
自上往下式堆化 ：将节点与其左右子节点比较，如果存在左右子节点大于该节点（大顶堆）或小于该节点（小顶堆），则将子节点的最大值（大顶堆）或最小值（小顶堆）与之交换
自下而上的堆化
```javascript const array = [3, 44, 38, 5, 47, 15, 36, 26, 1, 27, 46, 4, 19, 50, 48];

// 自下而上的建堆 const buildHeap = (arr, heapSize = 1) => { arr.unshift(null); // 在数组的第一个补个空元素，方便建堆 while (heapSize < arr.length - 1) { heapSize++; heapify(arr, heapSize) } arr.shift(); // 把空元素去除 }

// 堆化，比较元素与父元素的大小，依次往上排 const heapify = (arr, i) => { // 由于补了空元素，使得 Math.floor(i / 2) 就是第 i 项的父元素的位置 while (Math.floor(i / 2) > 0 && arr[i] < arr[Math.floor(i / 2)]) { swap(arr, i, Math.floor(i / 2)); i = Math.floor(i / 2) } }

const swap = (arr, i, j) => { const tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp }

buildHeap(array)

console.log(array); // [1, 3, 4, 5, 27, 15, 36, 44, 26, 47, 46, 38, 19, 50, 48]

<a name="LVRz2"></a>
### 自上而下的堆化
```javascript
const array = [3, 44, 38, 5, 47, 15, 36, 26, 1, 27, 46, 4, 19, 50, 48];
// 自上而下的建最大堆
const buildMaxHeap = (arr) => {
  const len = arr.length;
  // 找到元素的父元素
  for (let i = Math.floor(len / 2); i >= 0; i--) {
    heapify(arr, i);
  }
}
// 堆化：
const heapify = (arr, i) => {
  const len = arr.length;
  let left = 2 * i + 1;  // 左子节点
  let right = 2 * i + 2; // 右子节点
  let largest = i;       // 父元素
  if (left < len && arr[left] > arr[largest]) {
    largest = left;
  }
  if (right < len && arr[right] > arr[largest]) {
    largest = right;
  }
  if (largest !== i) {
    swap(arr, i, largest);
    heapify(arr, largest);
  }
}
// 交换元素
const swap = (arr, i, j) => {
  const tmp = arr[i];
  arr[i] = arr[j];
  arr[j] = tmp;
}
buildMaxHeap(array);
console.log(array); // [50, 47, 48, 26, 46, 19, 38,  5,  1, 27, 44,  4,15, 36,  3]

堆

简介

如何创建一个大（小）顶堆

插入式建堆

最小堆类的实现

原地建堆

自下而上的堆化