一、题目内容 简单

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

示例1：

给定二叉树 [3,9,20,null,null,15,7]， 3
/ \
9 20
/ \
15 7

返回它的最大深度 3 。

二、解题思路

我们要查找二叉树的最大深度，那么自然想到深度优先遍历。
我们找该节点的 左子树的最大深度 和 右子树的最大深度。
假如到了最底层，左右子树都为 null，那么返回 0。
如果不是最底层，那么返回该节点 左右子树的最大深度 + 1（返回给上一层，所以该节点的层数要加上）。
好了，这就是一个递归的思路。

三、具体代码

  1. /**
  2.  * @param {TreeNode} root
  3.  * @return {number}
  4.  */
  5. var maxDepth = function (root) {
  6.   const dfs = (node) => {
  7.     if (!node) return 0;
  8.     const leftDepth = dfs(node.left);
  9.     const rightDepth = dfs(node.right);
  10.     const depth = Math.max(leftDepth, rightDepth) + 1;
  11.     return depth;
  12.   }
  13.   return dfs(root);
  14. };
  15. /**
  16.  * 时间复杂度：O(n)
  17.  * 空间复杂度：O(height)，其中 height 表示二叉树的高度
  18.  */

四、其他解法

迭代法

使用迭代法的话，用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。
在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：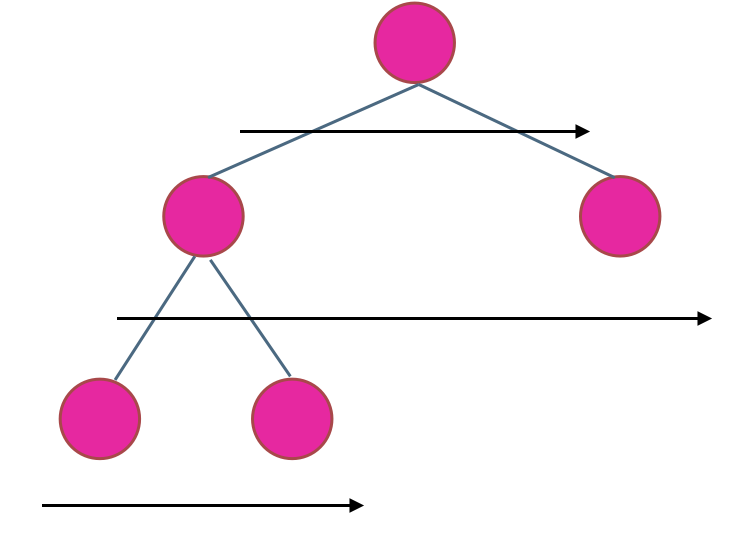
image.png

  1. /**
  2.  * @param {TreeNode} root
  3.  * @return {number}
  4.  */
  5. var maxDepth = function (root) {
  6.   if (!root) return 0
  7.   const queue = [[root, 1]]
  8.   let maxDeep = 0
  9.   while (queue.length) {
  10.     const [node, deep] = queue.shift()
  11.     maxDeep = Math.max(deep, maxDeep)
  12.     if (node.left) queue.push([node.left, deep + 1])
  13.     if (node.right) queue.push([node.right, deep + 1])
  14.   }
  15.   return maxDeep
  16. };
  1. /**
  2.  * @param {TreeNode} root
  3.  * @return {number}
  4.  */
  5. var maxDepth = function (root) {
  6.   if (!root) return 0
  7.   let maxDepth = 0
  8.   const queue = [root]
  9.   while (queue.length) {
  10.     const len = queue.length
  11.     maxDepth++
  12.     for (let i = 0; i < len; i++) {
  13.       const node = queue.shift()
  14.       if (node.left) queue.push(node.left)
  15.       if (node.right) queue.push(node.right)
  16.     }
  17.   }
  18.   return maxDepth
  19. };
  20. /**
  21.  * 时间复杂度：O(n)
  22.  * 空间复杂度：O(n)
  23.  */