一、题目内容 中等

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例1：

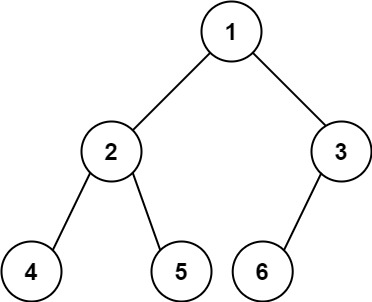
输入：root = [1,2,3,4,5,6] 输出：6 6. 完全二叉树的节点个数（222） - 图1

示例2：

输入：root = [] 输出：0

示例3：

输入：root = [1] 输出：1

提示：

  • 树中节点的数目范围是[0, 5 * 104]
  • 0 <= Node.val <= 5 * 104
  • 题目数据保证输入的树是 完全二叉树

进阶：遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

二、解题思路

暴力方式：一个个数。时间复杂度 O(n)

完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。
对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。
对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

三、具体代码

  1. /**
  2.  * @param {TreeNode} root
  3.  * @return {number}
  4.  */
  5. var countNodes = function (root) {
  6.   if (!root) return 0
  7.   const queue = [root]
  8.   let count = 0
  9.   while (queue.length) {
  10.     const len = queue.length
  11.     count += len
  12.     for (let i = 0; i < len; i++) {
  13.       const node = queue.shift()
  14.       if (node.left) queue.push(node.left)
  15.       if (node.right) queue.push(node.right)
  16.     }
  17.   }
  18.   return count
  19. };
  20. /**
  21.  * 时间复杂度: O（n）
  22.  * 空间复杂度: O（n）
  23.  */
  1. /**
  2.  * @param {TreeNode} root
  3.  * @return {number}
  4.  */
  5. var countNodes = function (root) {
  6.   if (!root) return 0
  7.   let left = root.left
  8.   let right = root.right
  9.   let leftDeep = 0, rightDeep = 0
  10.   while (left) {
  11.     left = left.left
  12.     leftDeep++
  13.   }
  14.   while (right) {
  15.     right = right.right
  16.     rightDeep++
  17.   }
  18.   if (leftDeep === rightDeep) return (2 << leftDeep) - 1
  20.   return countNodes(root.left) + countNodes(root.right) + 1
  21. };
  22. /**
  23.  * 时间复杂度：O(logn * logn)
  24.  * 空间复杂度：O(logn)
  25.  */

四、其他解法