7. 平衡二叉树（110）

一、题目内容 简单

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为： :::info 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。 :::

示例1：

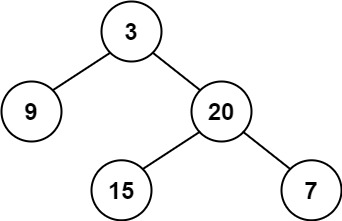
输入：root = [3,9,20,null,null,15,7] 输出：true

示例2：

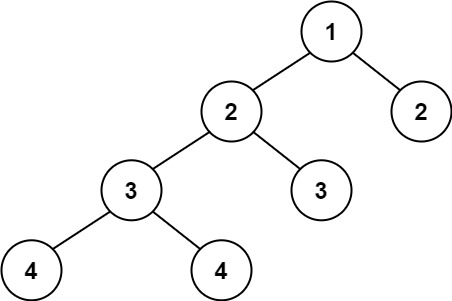
输入：root = [1,2,2,3,3,null,null,4,4] 输出：false

示例 3：

输入：root = [] 输出：true

提示：

• 树中的节点数在范围 [0, 5000] 内

• -104 <= Node.val <= 104

  二、解题思路

  这里强调一波概念：

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。

• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

但 leetcode 中强调的深度和高度很明显是按照节点来计算的，如图：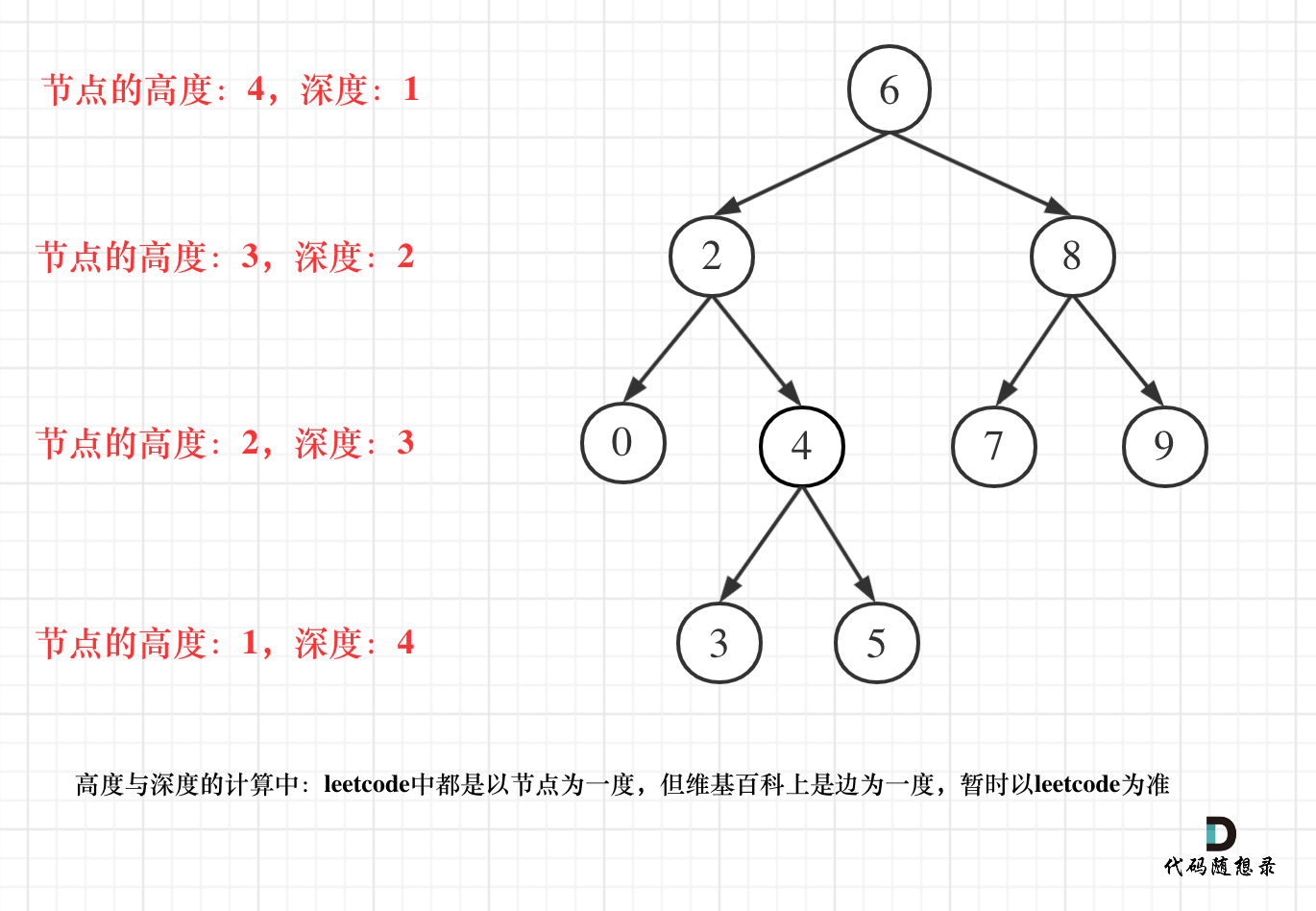

我们用递归计算的思路。递归嘛，化归到最少的元素，就 [4, 3 ,5]吧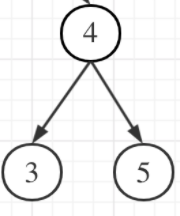

首先，从 4 开始，递归到 3 。那 3 往下了，没有 left、right，那么可以知道 3 的高度是 0。
返回，回到 4，拿到了左子树的高度，现在拿右子树的高度，同理，知道 5 的高度是 0。
回到 4，开始比较左右子树的高度差，是否小于等于 1。如果符合，那么该树是平衡二叉树。

const dfs = (node) => {
  if (!node) return 0
  const leftHeight = dfs(node.left)
  const rightHeight = dfs(node.right)
  if (Math.abs(leftHeight - rightHeight) < 2) return Math.max(leftHeight, rightHeight) + 1
  // 不符合平衡二叉树，就会走到这里
}

但是等等，这样就完了吗，如果，下面拿到了不符合的情况，怎么向上层传递？
如果不符合，我们需要给点标志吧，那就用 -1 吧。 当接受到 -1，就让他一直往上冒泡就好了。

const dfs = (node) => {
  if (!node) return 0
  const leftHeight = dfs(node.left)
  if (leftHeight === -1) return -1    // 往上冒泡
  const rightHeight = dfs(node.right)
  if (rightHeight === -1) return -1 // 往上冒泡
  if (Math.abs(leftHeight - rightHeight) < 2) return Math.max(leftHeight, rightHeight) + 1
  // 不符合平衡二叉树，就会走到这里
  return -1
}

三、具体代码

/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isBalanced = function (root) {
  if (!root) return true
  const dfs = (node) => {
    if (!node) return 0
    const leftHeight = dfs(node.left)
    if (leftHeight === -1) return -1
    const rightHeight = dfs(node.right)
    if (rightHeight === -1) return -1
    if (Math.abs(leftHeight - rightHeight) < 2) return Math.max(leftHeight, rightHeight) + 1
    return -1
  }
  return dfs(root) === -1 ? false : true
};

四、其他解法