title: LTR技术用于精排
subtitle: Learning to Rank
date: 2020-07-21
author: NSX
catalog: true
tags:
- 技术
- Learning to Rank
- 什么是排序学习?
- 排序评价指标(NDCG)
- LTR三种训练方式(Pointwise/Pairwise/Listwise)
- LTR面临的三大挑战
- LTR公开数据集
- LTR开源库
- LTR在大厂的应用
- LTR检索排序探索与实践
- 检索召回
- 精准排序⭐️
- 拓展:LTR常用算法详细介绍
- Pointwise Ranker(LR / GBDT / DNN)
- Pairwise Ranker(RankSVM / RankNet / LambdaRank / LambdaMART)
- Listwise Ranker(LambdaRank / LambdaMART)
前言
Elasticsearch 内部有几种不同的算法来评估相关度(relevance):TF-IDF、BM25、BM25F等。但是这种模型 #card=math&code=f%28q%2Cd%29&id=uDNCc) 其实是简单的概率模型,评估 query 在 doc 中出现的位置、次数、频率等因素,但是不能有效的根据用户反馈(点击/停留时间)来持续优化搜索结果。比如说用户搜索了某些关键词,点击了某些结果,而这些结果并不是排在最前面的,但确实是用户最想要的。那有没有什么方法可以使它们排在前面呢?
Learning to Rank
信息展示个性化的典型应用主要包括搜索列表、推荐列表、广告展示等等。很多人不知道的是,看似简单的个性化信息展示背后,涉及大量的数据、算法以及工程架构技术,这些足以让大部分互联网公司望而却步。究其根本原因,个性化信息展示背后的技术是排序学习问题(Learning to Rank)。——-深入浅出排序学习:写给程序员的算法系统开发实践
什么是排序学习?
传统的排序方法通过构造相关度函数,按照相关度对于每一个文档进行打分,得分较高的文档,排的位置就靠前。但是,随着相关度函数中特征的增多,使调参变得极其的困难。所以我们自然而然的想到使用机器学习来优化搜索排序,这就导致了排序学习 LTR (Learning to rank)的诞生。
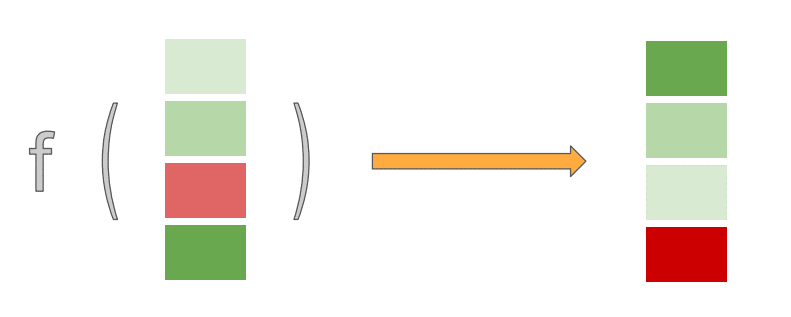
可以将LTR归纳为这样一个问题:基于q-d特征向量,通过机器学习算法训练来学习一个最佳的拟合公式,从而对文档打分并排序。在这个过程中,可以选定学习器(如神经网络、树模型、线性模型等),去自动学习对应的权重应该是多少?学习权重的时候需要确定损失函数,以最小化损失函数为目标进行优化即可得到学习器的相关参数。损失函数的作用相当于告诉学习器应该沿着那个方向去优化,才能保证获得最优的权重。
LTR的目标
排序学习是机器学习在信息检索系统里的应用,其目标是构建一个排序模型,根据用户的行为反馈来对多路召回的 item 进行打分,从而实现对多个条目的排序。LTR 相比传统的排序方法,优势有很多:
- 整合大量复杂特征并自动进行参数调整,自动学习最优参数;
- 融合多方面的排序影响因素,降低了单一考虑排序因素的风险;
- 能够通过众多有效手段规避过拟合问题。
- 实现个性化需求(推荐)
- 多种召回策略的融合排序推荐(推荐)
排序评价指标
Binary Relevance
Precision and Recall(P-R)
本评价体系通过准确率(Precision)和召回率(Recall)两个指标来共同衡量列表的排序质量。对于一个请求关键词,所有的文档被标记为相关和不相关两种。
Precision的定义如下:

Recall的定义如下:
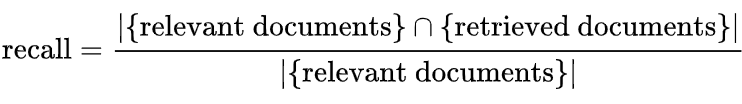
Mean Average Precision (MAP):
Average Precision (AP):
%3D%5Cfrac%7B%5Csum%7Bk%3D1%7D%5E%7Bm%7D%20P%20%40%20k%20%5Ccdot%20I%5Cleft%5C%7Bl%7B%5Cpi-1%7D(k)%3D1%5Cright%5C%7D%7D%7Bm%7B1%7D%7D%0A#card=math&code=%5Cmathrm%7BAP%7D%28%5Cpi%2C%20l%29%3D%5Cfrac%7B%5Csum%7Bk%3D1%7D%5E%7Bm%7D%20P%20%40%20k%20%5Ccdot%20I%5Cleft%5C%7Bl%7B%5Cpi-1%7D%28k%29%3D1%5Cright%5C%7D%7D%7Bm%7B1%7D%7D%0A&id=DS8e3)
如果想要衡量一个模型的好坏,就需要对多次排序结果的AP值求平均,这样就得到MAP. MAP它反映了查询结果中前 k 名的相关性。
MRR(Mean Reciprocal Rank)
对于给定查询q,如果第一个相关的文档的位置是R(q),则%3D1%2FR(q)%3Drank_i#card=math&code=MRR%28q%29%3D1%2FR%28q%29%3Drank_i&id=MuTKk)。
Graded Relevance
Discounted Cumulative Gain(DCG)
P-R的有两个明显缺点:
- 所有文章只被分为相关和不相关两档,分类显然太粗糙。
- 没有考虑位置因素。
DCG解决了这两个问题。对于一个关键词,所有的文档可以分为多个相关性级别,这里以rel1,rel2…来表示。文章相关性对整个列表评价指标的贡献随着位置的增加而对数衰减,位置越靠后,衰减越严重。
系统通常为某用户返回一个item列表,假设列表长度为K,这时可以用NDCG@K评价该排序列表与用户真实交互列表的差距。
解释:
- Gain: 表示列表中每一个item的相关性分数(标签增益)
%3D%7B2%5E%7Br(i)%7D-1%7D%0A#card=math&code=Gain%28i%29%3D%7B2%5E%7Br%28i%29%7D-1%7D%0A&id=tN3r6)
其中,%7D#card=math&code=%7Br%28i%29%7D&id=APBMy)表示第 i 个文档的真实相关度;
- Cumulative Gain:表示对K个item的Gain进行累加
%0A#card=math&code=%5Cmathrm%7BCG%7D%40%7BK%7D%3D%5Csum_%7Bi%3D1%7D%5E%7BK%7D%20Gain%28i%29%0A&id=wqVaG)
- Discounted Cumulative Gain (DCG@K):考虑排序顺序的因素,使得排名靠前的item增益更高,对排名靠后的item进行折损 (把每个位置对应的标签增益乘以位置折扣,最后累加到一起):
位置折扣 #card=math&code=%5Ceta%28i%29&id=YT4kC) 的常用设置:
%3D%5Cfrac%7B1%7D%7B%5Clog%20(j%2B1)%7D%0A#card=math&code=n%28j%29%3D%5Cfrac%7B1%7D%7B%5Clog%20%28j%2B1%29%7D%0A&id=fJ2DS)
从中可以看出DCG的一个特性:排名靠前的doc增益更高,对排名靠后的doc进行折损
- Normalized Discounted Cumulative Gain:DCG能够对一个用户的推荐列表进行评价,如果用该指标评价某个推荐算法,需要对所有用户的推荐列表进行评价,而不同用户之间的DCG相比没有意义(不同用户兴趣不同,对同样的item排名前后不同)。所以要对不同用户的指标进行归一化,自然的想法就是对每个用户计算一个理想情况(或者说是实际情况)下的DCG分数,用IDCG表示,然后用每个用户的DCG与IDCG之比作为每个用户归一化后的分值,最后对每个用户取平均得到最终的分值,即NDCG。
IDCG的定义如下: %7D-1%7D%7B%5Clog%20%7B2%7D(i%2B1)%7D%0A#card=math&code=%5Cmathrm%7BIDCG%7D%7B%5Cmathrm%7BK%7D%7D%3D%5Csum%7Bi%3D1%7D%5E%7B%7CR%20E%20L%7C%7D%20%5Cfrac%7B2%5E%7Br%28i%29%7D-1%7D%7B%5Clog%20%7B2%7D%28i%2B1%29%7D%0A&id=KnVmH)
DCG中的相关性得分#card=math&code=r%28i%29&id=f7LnV)是根据预测概率,来对相关度label进行排序;
IDCG中的相关性得分#card=math&code=r%28i%29&id=SWRQY)是根据实际label大小,来对相关度label进行排序;
图示: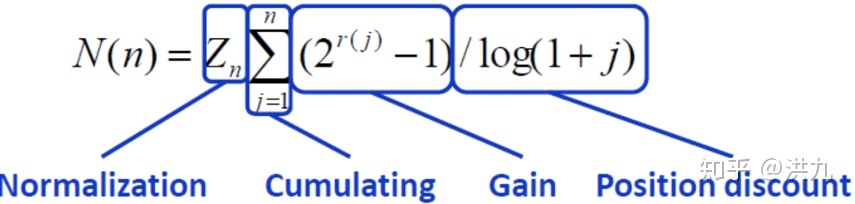
PS: NDCG(Normalized Discounted Cumulative Gain) 是一种综合考虑模型排序结果和真实序列之间的关系的一种指标,也是最常用的衡量排序结果的指标,越相关的结果排到越前,分数越高;
- NDCG的形象理解 https://blog.csdn.net/anshuai_aw1/article/details/83117012
- NDCG的Python实现可参考链接
Expected Reciprocal Rank(ERR)
与DCG相比,除了考虑位置衰减和允许多种相关级别(以R1,R2,R3…来表示)以外,ERR更进了一步,还考虑了排在文档之前所有文档的相关性。举个例子来说,文档A非常相关,排在第5位。如果排在前面的4个文档相关度都不高,那么文档A对列表的贡献就很大。反过来,如果前面4个文档相关度很大,已经完全解决了用户的搜索需求,用户根本就不会点击第5个位置的文档,那么文档A对列表的贡献就不大。ERR的定义如下:
%20R%7Br%7D%0A#card=math&code=E%20R%20R%3D%5Csum%7B%5Cmathrm%7Br%7D%3D1%7D%5E%7B%5Cmathrm%7Bn%7D%7D%20%5Cfrac%7B1%7D%7B%5Cmathrm%7Br%7D%7D%20%5Cprod%7B%5Cmathrm%7Bi%7D%3D1%7D%5E%7B%5Cmathrm%7Br%7D-1%7D%5Cleft%281-R%7B%5Cmathrm%7Bi%7D%7D%5Cright%29%20R_%7Br%7D%0A&id=Z2BUP)
LTR训练算法
参考《推荐系统中排序学习的三种设计思路》
在训练阶段输入是n个query对应的doc集合,通常数据来源有两种,一种是人工标注,即通过对实际系统中用户query返回的doc集合进行相关性标注,标签打分可以是三分制(相关,不相关,弱相关),也可以是更细的打分标准。另外一种是点击日志中获取,通过对一段时间内的点击信息进行处理获得优质的点击数据。这些输入的doc的表示形式是多个维度的特征向量,特征的设计也尤其重要,对网页系统检索而言,常用的有查询与文档匹配特征,其中细化了很多角度的匹配,比如紧密度匹配,语义匹配,精准匹配等等,还有通过将文档分为不同域后的各个域的匹配特征,关键词匹配特征,bm系列特征, 以及通过dnn学习得到的端到端的匹配特征。
通过排序模型的不断迭代,当一个用户输入一个query之后,排序系统会根据现有模型计算各个doc在当前特征下的得分,并根据得分进行排序返回给用户。
Learning to rank需要以排序的评价指标作为优化目标,来让整体排序效果更佳。但是评判排序好坏的这些指标的特点是不平滑、不连续(?),无法求梯度,因此无法直接用梯度下降法求解。所以诞生了3种近似求解的训练方法(优化策略):
- Pointwise
- Pairwise
- Listwise
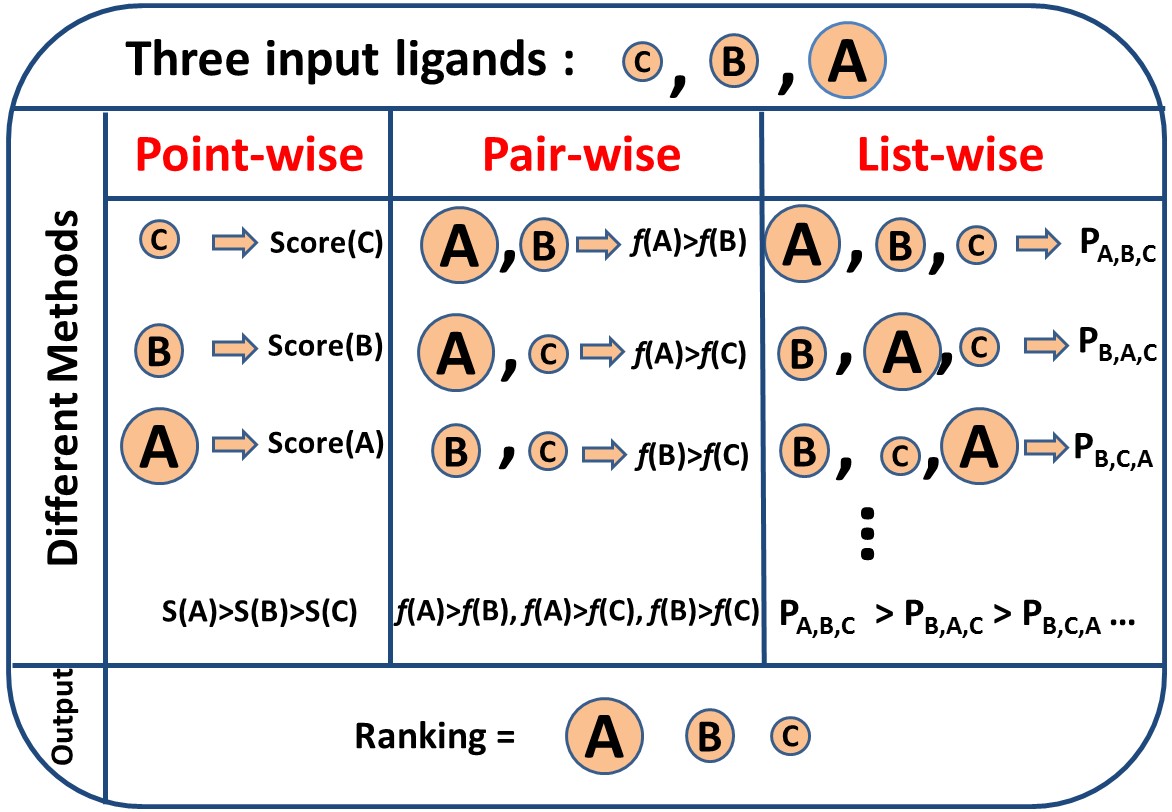
其中pointwise将其转化为多类分类或者回归问题,pairwise将其转化为pair分类问题,Listwise为对查询下的一整个候选集作为学习目标,三者的区别在于loss不同、以及相应的标签标注方式和优化方法的不同。

Pointwise
该方法将排序问题转化为分类问题或者回归问题,只考虑query和单个文档的绝对相关度作为标签,而不考虑其他文档和query的相关度。比如标签有三档,问题就变为多类分类问题,模型有McRank,svm,最大熵等。另一种思想是将query与doc之间的相关程度作为分数利用回归模型拟合,经典回归模型有线性回归,dnn,mart等。
输入数据应该是如下的形式:

- 输入空间:doc 的特征向量
#card=math&code=%28x_i%2Cy%29&id=KfaeX)
- 输出空间:每个doc的相关性分数
损失函数:回归loss,分类loss
%2Cy)%3D%5Csum%7Bi%3D1%7D%5En%7Bl(f(x_i)%2Cy_i)%7D%3D%5Csum%7Bi%3D1%7D%5En%7Bf(xi)log(y_i)%7D%0A#card=math&code=L%28f%28x%29%2Cy%29%3D%5Csum%7Bi%3D1%7D%5En%7Bl%28f%28xi%29%2Cy_i%29%7D%3D%5Csum%7Bi%3D1%7D%5En%7Bf%28x_i%29log%28y_i%29%7D%0A&id=OwaOz)
Pointwise 方法存在的问题:
Pointwise 方法通过优化损失函数求解最优的参数,可以看到 Pointwise 方法非常简单,工程上也易实现,但是 Pointwise 也存在很多问题:
- Pointwise 只考虑单个文档同 query 的相关性,没有考虑文档间的关系,然而排序追求的是排序结果,并不要求精确打分,只要有相对打分即可;
- 通过分类只是把不同的文档做了一个简单的区分,同一个类别里的文档则无法深入区别,虽然我们可以根据预测的概率来区别,但实际上,这个概率只是准确度概率,并不是真正的排序靠前的预测概率;
- Pointwise 方法并没有考虑同一个 query 对应的文档间的内部依赖性。一方面,导致输入空间内的样本不是 IID 的,违反了 ML 的基本假设,另一方面,没有充分利用这种样本间的结构性。其次,当不同 query 对应不同数量的文档时,整体 loss 将容易被对应文档数量大的 query 组所支配,应该每组 query 都是等价的才合理。
- 很多时候,排序结果的 Top N 条的顺序重要性远比剩下全部顺序重要性要高,因为损失函数没有相对排序位置信息,这样会使损失函数可能无意的过多强调那些不重要的 docs,即那些排序在后面对用户体验影响小的 doc,所以对于位置靠前但是排序错误的文档应该加大惩罚。
Pairwise
Pairwise是目前比较流行的方法,相对pointwise他将重点转向文档顺序关系。比如对于query 1返回的三个文档 doc1,doc2,doc3, 有三种组对方式,

- 输入空间:同一查询的一对文档
#card=math&code=%28x_i%2Cx_j%2Cy%29&id=k78rj)
- 输出空间:两个文档的相对关系
- 损失函数:铰链损失( hinge loss)、交叉熵损失( cross entropy loss)
ir 领域一个被广泛使用的 pairwise loss 就是 Hingle Loss,其基本形式为:%3D%5Csum%7Bi%7D%20%5Csum%7B%5C%7Bj%2C%20k%5C%7D%2C%20y%7Bi%2C%20j%7D%20%5Csucc%20y%7Bi%2C%20k%7D%7D%20%5Cmax%20%5Cleft(0%2C1-f%5Cleft(q%7Bi%7D%2C%20d%7Bi%2C%20j%7D%5Cright)%2Bf%5Cleft(q%7Bi%7D%2C%20d%7Bi%2C%20k%7D%5Cright)%5Cright)%0A#card=math&code=%5Cmathcal%7BL%7D%28f%20%3B%20%5Cmathcal%7BQ%7D%2C%20%5Cmathcal%7BD%7D%2C%20%5Cmathcal%7BY%7D%29%3D%5Csum%7Bi%7D%20%5Csum%7B%5C%7Bj%2C%20k%5C%7D%2C%20y%7Bi%2C%20j%7D%20%5Csucc%20y%7Bi%2C%20k%7D%7D%20%5Cmax%20%5Cleft%280%2C1-f%5Cleft%28q%7Bi%7D%2C%20d%7Bi%2C%20j%7D%5Cright%29%2Bf%5Cleft%28q%7Bi%7D%2C%20d%7Bi%2C%20k%7D%5Cright%29%5Cright%29%0A&id=mQGyk)
还有一个 Pairwise 的损失函数就是上文提到的 RankNet 中使用的基于交叉熵的损失函数及其改进型 LambdaRank,但是应用似乎并不广泛,可能原因是在 IR 的 Matching 任务中,query 对应的 doc 之间没有很明显的等级关系,而通常是 0-1 的相关与否,并且多数只有一个正样本,因此 RankNet 中的 Pairwise Loss 并不能有效的起到作用。%20%5Cln%20(1-a)%5D%0A#card=math&code=C%3D-%5Cfrac%7B1%7D%7Bn%7D%20%5Csum_%7Bx%7D%5By%20%5Cln%20a%2B%281-y%29%20%5Cln%20%281-a%29%5D%0A&id=MWu9O)
式中,x 表示样本; n 表示样本总数; y 为期望输 出; a 为神经元实际输出,并且交叉熵具有非负性,当 a 和 y 接近时,损失函数接近于 0。 - 常用算法:Ranking SVM (ICANN 1999)、RankBoost (JMLR 2003)、RankNet (ICML 2005)、lambdaRank (NIPS 2006)、LambdaMART (inf.retr 2010)
这里讨论下,关于人工标注标签怎么转换到 pairwise 类方法的输出空间:
Pairwise 方法的输出空间应该是包括所有文档的两两文档对的偏序关系(pairwise preference),其取值为 {+1,−1},+1 表示文档对中前者更相关,-1 则表示文档对中后者更相关,我们可以把不同类型的人工标注的标签转换到 Pairwise 的真实标签。
- 如果标注直接是相关度
(即单点标注),则文档对
#card=math&code=%28xu%2Cx_v%29&id=RIWvn) 的真实标签定义为 ,相关度打分
,
- 如果标注是 pairwise preference
,则 doc pair
#card=math&code=%28xu%2Cx_v%29&id=Rd464) 的真实标签定义为 
- 如果标注是整体排序 π,则 doc pair
#card=math&code=%28xu%2Cx_v%29&id=AdoSq) 的真实标签定义为 
Pairwise 方法存在的问题:
Pairwise 方法通过考虑两两文档之间的相关对顺序来进行排序,相比 Pointwise 方法有明显改善。但 Pairwise 方法仍有如下问题:
- 使用的是两文档之间相关度的损失函数,而它和真正衡量排序效果的指标之间存在很大不同,甚至可能是负相关的,如可能出现 Pairwise Loss 越来越低,但 NDCG 分数也越来越低的现象。
- 只考虑了两个文档的先后顺序,且没有考虑文档在搜索列表中出现的位置,导致最终排序效果并不理想。
- 不同的查询,其相关文档数量差异很大,转换为文档对之后,有的查询可能有几百对文档,有的可能只有几十个,这样不加均一化地在一起学习,模型会优先考虑文档对数量多的查询,减少这些查询的 loss,最终对机器学习的效果评价造成困难。
- Pairwise 方法的训练样例是偏序文档对,它将对文档的排序转化为对不同文档与查询相关性大小关系的预测;因此,如果因某个文档相关性被预测错误,或文档对的两个文档相关性均被预测错误,则会影响与之关联的其它文档,进而引起连锁反应并影响最终排序结果。
Listwise
Pointwise将训练集里每一个文档当做一个训练实例,pairwise方法将同一个査询的搜索结果里任意两个文档对作为一个训练实例,Listwise方法是将每一个查询对应的所有搜索结果列表整体作为一个训练实例,根据这些训练样例训练得到最优评分函数 #card=math&code=F%28%29&id=e4fgO)
- 输入空间:Set of documents
- 输出空间:Ranked list
- 假设空间:Sort function
#card=math&code=F%28x%29&id=KjsPt)
- 损失函数:常见的模型比如ListNet使用正确排序与预测排序的排列概率分布之间的KL距离(交叉熵)作为损失函数,LambdaMART的框架其实就是MART,主要的创新在于中间计算的梯度使用的是Lambda,将IR评价机制如NDCG这种无法求导的IR评价指标转换成可以求导的函数,并且富有了梯度的实际物理意义
PS: 我们的输入是整个List,直接优化NDCG。但NDCG非凸且不可导,该怎么办呢? 既然无法定义一个符合要求的loss,那就直接定义一个符合我们要求的梯度。*策略算法工程师之路-损失函数设计

上述推导过程就不必细看了,直接看最后的结果。

而我们可以根据业务需求自定义:
既然如此回到我们的优化目标NDCG,就可以定义:
为对特定List,将Ui,Uj的位置调换,NDCG值的变化。所以我们就做到在NDCG非凸且不可导的情况下直接优化NDCG了。
- 常用算法:AdaRank (SIGIR 2007)、SVM-MAP (SIGIR 2007)、SoftRank (LR4IR 2007)、ListNet (ICML 2007)、LambdaMART (inf.retr 2010)(也可以做Listwise)
推荐中使用较多的 Listwise 方法是 LambdaMART(LambdaMART是LambdaRank的提升树版本,而LambdaRank又是基于pairwise的RankNet。因此LambdaMART本质上也是属于pairwise排序算法,只不过引入Lambda梯度后,还显示的考察了列表级的排序指标,如NDCG等,因此,也可以算作是listwise的排序算法!!!)
列表法和配对法的中间解法
第三种思路某种程度上说是第一种思路的一个分支,因为很特别,这里单独列出来。其特点是在纯列表法和配对法之间寻求一种中间解法。具体来说,这类思路的核心思想,是从 NDCG 等指标中受到启发,设计出一种替代的目标函数。这一步和刚才介绍的第一种思路中的第一个方向有异曲同工之妙,都是希望能够找到替代品。
找到替代品以后,接下来就是把直接优化列表的想法退化成优化某种配对。这第二步就更进一步简化了问题。这个方向的代表方法就是微软发明的 LambdaRank 以及后来的 LambdaMART。微软发明的这个系列算法成了微软的搜索引擎 Bing 的核心算法之一,而且 LambdaMART 也是推荐领域中可能用到一类排序算法。
三类训练方法对比
在工业界用的比较多的应该还是Pairwise,因为构建训练样本相对方便,并且复杂度也还可以。
| L2R | 优点 | 缺点 | 输入 | 时间复杂度 |
|---|---|---|---|---|
| PointWise | 简单,只需以单个文档作为训练数据 | 只考虑单个文档同 query 的相关性,没有考虑文档间的关系 | ||
| PairWise | 对文档对进行分类,得到文档集的偏序关系 | 只考虑每对文档之间的偏序关系 预测错误的文档对可能会引起连锁反应 无法衡量真正的排序指标 |
||
| ListWise | 直接对文档结果进行优化,效果最好 | 很难找到合适的优化算法进行求解 |
 |
 |
|---|---|
在线排序架构三大挑战
在线排序架构主要面临三方面的挑战:特征、模型和召回。
- 特征挑战包括特征添加、特征算子、特征归一化、特征离散化、特征获取、特征服务治理等。
- 模型挑战包括基础模型完备性、级联模型、复合目标、A/B实验支持、模型热加载等。
- 召回挑战包括关键词召回、LBS召回、推荐召回、粗排召回等。
三大挑战内部包含了非常多更细粒度的挑战,孤立地解决每个挑战显然不是好思路。在线排序作为一个被广泛使用的架构值得采用领域模型进行统一解决。Domain-driven design(DDD)的三个原则分别是:领域聚焦、边界清晰、持续集成。
基于以上分析,我们构建了三个在线排序领域模型:召回治理、特征服务治理和在线排序分层模型。
召回治理
召回就是找到用户可能喜欢的几百条资讯,召回总体而言分成四大类:
- 关键词召回,我们采用Elasticsearch解决方案。
- 距离召回,我们采用K-D tree的解决方案。
- 粗排召回。
- 推荐类召回。
特征服务治理
传统的视角认为特征服务应该分为用户特征(User)、查询特征(Query)和文档特征(Doc),如下图:
这是比较纯粹的业务视角,并不满足DDD的领域架构设计思路。由于特征数量巨大,我们没有办法为每个特征设计一套方案,但是我们可以把特征进行归类,为几类特征分别设计解决方案:
- Doc特征:类别category_id、总体点击率、最近一周点击率、发布时间、更新时间-新鲜度、标题向量、文章长度、来源source、点赞数、点击反馈、高亮字数
- Query-Doc相关性特征:向量相似度(cosine、TF-IDF、vsm、BOW)、query 和 doc 之间的词共现特性、点击次数和点击率、bm25
- context特征:页数、曝光顺序位置SearchOrder、请求时间段等;
- 后延统计特征:在一段时间内的点击数和点击率CTR、交叉特征
- 稀疏特征:docID、itemID、answerID、pageNum、pageSize、baseCode、botCode、projectCode
其中ID类特征和交叉特征是离散型特征,相关特征和统计特征是连续型特征. ID 特征也是有重要意义的,在特征工程中应该予以考虑。用户特征和Query特征暂不考虑。
在线排序分层模型
如下图所示,典型的排序流程包含六个步骤:场景分发(Scene Dispatch)、流量分配(Traffic Distribution)、召回(Recall)、特征抽取(Feature Retrieval)、预测(Prediction)、排序(Ranking)等等。

智能重排序的实现方案与算法原理
- 事先计算型智能重排序
重排序引擎通过处理用户行为日志,并基于用户兴趣将用户聚类后,再构建排序模型,为每一个聚类生成唯一的排序结果并存放到数据库中,当用户在产品(即APP)上访问该列表时,智能重排序web服务模块将该列表的排序结果取出来并在前端展现给用户。 - 实时装配型智能重排序
近实时地计算出用户特征向量与每个标的物特征向量的内积(该内积即用户对该标的物的偏好得分),并对列表中所有标的物的偏好得分降序排列- FAISS向量近似搜索方案
- TensorFlow Serving方案,需要事先训练出一个排序模型,将用户特征和item特征按照某种方式灌入该模型
- 先对所有标的物排序再筛选
对标的物也只需要计算一次排序,并且排序结果也可以事先存储起来。在提供服务时只需要进行过滤就够了
排序任务的公开数据集
公开的数据集 (LETOR datasets)
LTR开源库
- LEROT:用python 在线学习编写排名框架。另外,数据集的列表也不那么详细,但列表更长:https://bitbucket.org/ilps/lerot#rst-header-data
- IPython演示 to Rank.ipynb)学习排名
- LambdaRank的实现 (在Python中专门用于kaggle排名竞赛)
- TF-Ranking ⭐2K
- Github:TensorFlow Ranking
- Steps to get started:Tutorial: TF-Ranking for sparse features
- 论文:TF-Ranking: Scalable TensorFlow Library for Learning-to-Rank
TF-Ranking 是 google 在 2018 年底开源的基于 tf 设计的 ltr 算法框架,目的是形成可扩展、适用于系数特征的 dnn 的 ltr 算法。TF-Ranking提供了一个统一的框架,包含了一系列state-of-arts排序学习算法,并提供了灵活的API,支持了多种特性,如:自定义pairwise 或 listwise 损失函数,评分函数,指标等;非平滑排序度量指标的直接优化LamdaLoss;无偏的排序学习方法。同时,TF-Ranking还能够利用Tensorflow提供的深度学习特性,如稀疏特征的embedding,大规模数据扩展性、泛化性等。
- XGBoost
早期版本的 XGBoost 通过目标函数(objective) 中 rank:pairwise 来实现 ltr 任务,官方的教程也是这么写的。这里是一种使用交叉熵的 pairwise 实现,可以看做是不考虑 [公式] 的 LambdaMART。大概是 18 年(记不清了)的时候增加了 rank:ndcg 的实现,也就是完整版的 LambdaMART 实现。配合上 xgboost 在 gbm 基础上的各种优化,理论上 xgboost 中的 LambdaMART 可以有着比 Ranklib 更好的性能。
- lightGBM ⭐12.2K
另一个非常著名的 gbm 实现就是有微软开源的 lightGBM,lightGBM 当年在已有 xgboost 在前的情况下通过一系列对模型具体实现的优化从而在速度上占据了优势。
- Pyltr ⭐346
Python learning to rank (LTR) toolkit - Ranknet ⭐187
My (slightly modified) Keras implementation of RankNet and PyTorch implementation of LambdaRank. - Awesome Search ⭐68
it’s all about search and its awesomeness - DeepCTR ⭐4.6K
DeepCTR是基于深度学习的CTR模型的易于使用,模块化和可扩展的软件包,以及许多可用于轻松构建自定义模型的核心组件层。包含Wide & Deep、DeepFM、Deep & Cross Network、Deep Interest Network、DIEN、FiBiNET等Models。
LTR模型在大厂的应用
- WSDM Cup 2020 DiggSci 2020赛题冠军队伍成员
- 给了一堆LTR相关的资料链接和大厂的实践指南!
- 信息量非常大!
大众点评搜索基于知识图谱的深度学习排序实践—-LambdaDNN
由GBDT升级到DNN模型,这么做主要是考虑到两点:
- 数据量变大之后,DNN能够实现更复杂的模型,而GBDT的模型容量比较有限。
- 新的研究成果都是基于深度学习的研究,采用深度神经网络之后可以更好的应用新的研究成果,比如后面介绍的多目标排序。
DNN排序模型整体是在谷歌开源的TF-Ranking[1] 框架的基础上开发,包括特征输入、特征转化、模型打分和损失计算等几个独立的模块。深度模型之Wide&Deep、DeepFM模型、DCN模型、DIN模型、DIEN模型*Pointwise*类型的语义相似模型,如文本匹配库matchzoo,构建MV-LSTM、DRMM和DUET这三类使用较多的文本匹配模型
Unbias LTR
在使用用户点击日志作为训练数据时,点击日志中的一些噪声会对训练带来一定的负面影响。其中最常见的噪声就是Position bias,由于用户的浏览行为是从上到下的,所以同样的内容出现的位置越靠前越容易获得点击。解决方案:对Position bias建模。用户实际点击 = 真实点击率+ Position Bias- Context Aware LTR
借鉴了CV 中的 SE Block[4] 结构 - 尝试融合模型 Ensemble( BERT(pairwise) + LightGBM(pairwise) )
``` WSDM Cup 2020检索排序评测任务第一名经验总结 https://www.zhuanzhi.ai/document/24ad9f7f873da90dc072b0c777e1acfe
开源的代码,也包括了集成的部分 https://github.com/myeclipse/wsdm_cup_2020_solution
<a name="cc000168"></a># 检索排序探索与实践❤❤❤> [WSDM Cup 2020检索排序评测任务第一名经验总结](https://www.zhuanzhi.ai/document/24ad9f7f873da90dc072b0c777e1acfe)检索排序包括“检索召回”和“精准排序”两个阶段。其中,检索召回阶段负责从候选集中高效快速地召回候选Documents,从而缩减问题规模,降低排序阶段的复杂度,此阶段注重召回算法的效率和召回率;精准排序阶段负责对召回数据进行重排序,采用Learning to Rank相关策略进行排序最优解求解。典型的搜索排序算法框架如下图所示,分为线下训练和线上排序两个部分。模型包括相关性模型、时效性模型、个性化模型和**点击模型**等。特征包括Query特征、Doc特征、User特征和Query-Doc匹配特征等。日志包括展现日志、点击日志和Query日志。**点击模型介绍**点击模型又称为**点击调权**,搜索引擎根据用户对搜索结果的点击,可以挖掘出哪些结果更符合查询的需求。点击模型基于如下基本假设:1. 用户的浏览顺序是从上至下的。2. 需求满足好的结果,整体点击率一定高。3. 同一个query下,用户点击的最后一个结果之后的结果,可以假设用户已经不会去查看了(一定程度上减弱了位置偏见)。4. 用户进行了翻页操作,或者有效的query变换,则可以认为前页的结果用户都浏览过,并且不太满意。5. 用户点击的结果,如果引发后继的转化行为(比如电商搜索中的加购物车),则更有可能是用户满意的结果。<a name="70b243b6"></a>## 检索召回(Recall)- **目标任务**:使用高效的匹配算法对候选集进行粗筛,为后续精排阶段缩减候选排序的数据规模。- **性能要求**:召回阶段的方案需要权衡召回覆盖率和算法效率两个指标,一方面召回覆盖率决定了后续精排算法的效果上限,另一方面单纯追求覆盖率而忽视算法效率则不能满足评测时效性的要求。- **检索召回方案** :比赛过程中对比实验了两种召回方案,基于“文本语义向量表征“和“基于空间向量模型 + Bag-of-Ngram”。由于本任务文本普遍较长且专有名词较多等数据特点,实验表明“基于空间向量模型 + Bag-of-Ngram”的召回方案效果更好,下表中列出了使用的相关模型及其实验结果(recall@200)。可以看到相比于传统的BM25和TFIDF等算法,F1EXP、F2EXP等公理检索模型(Axiomatic Retrieval Models)可以取得更高的召回覆盖率,该类模型增加了一些公理约束条件,例如基本术语频率约束, 术语区分约束和文档长度归一化约束等等。为了提升召回算法的效果,我们使用倒排索引技术对数据进行建模,然后在此基础上实现了F1EXP、DFR、F2EXP、BM25、TFIDF等多种检索算法,极大了提升了召回部分的运行效率。为了平衡召回率和计算成本,最后使用F1EXP、BM25、TFIDF 3种算法各召回50条结果融合作为后续精排候选数据,在验证集上测试,召回覆盖率可以到70%。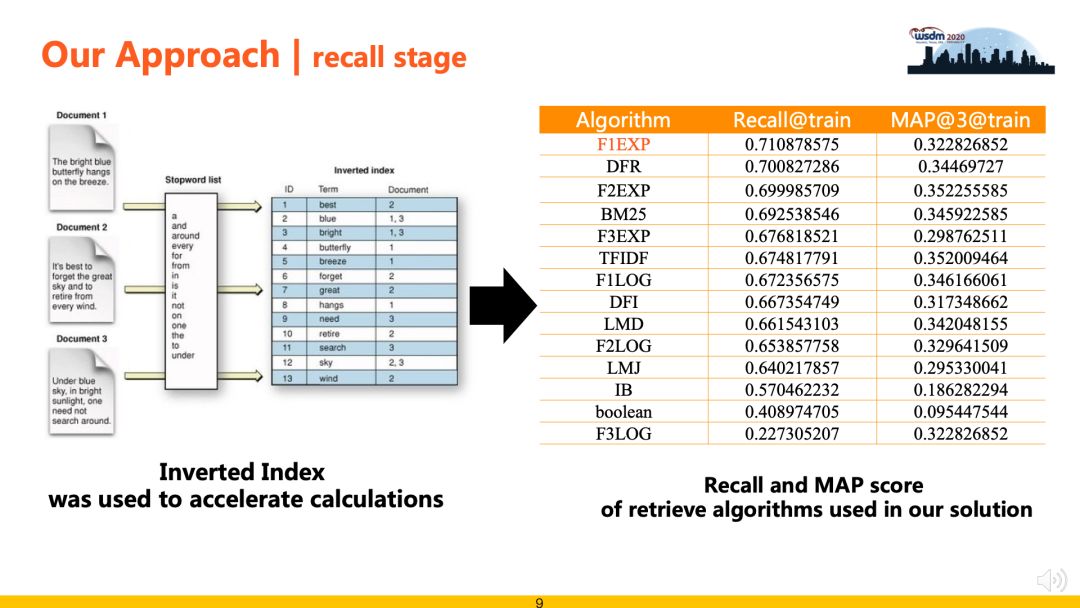<a name="99c10de0"></a>## 精准排序(Ranking)> 参考 [jiangnanboy / learning_to_rank](https://github.com/jiangnanboy/learning_to_rank)> [利用lightgbm做(learning to rank)排序学习](https://my.oschina.net/u/4585416/blog/4398683/print)从整体框架的角度看,当用户每次请求时,系统就会将当前请求的数据写入到日志当中,利用各种数据处理工具对原始日志进行清洗,格式化,并存储到文件中。在训练时,我们利用特征工程,从处理过后的数据集中选出训练、测试样本集,并借此进行线下模型的训练和预估。我们采用多种机器学习算法,并通过线下AUC、NDCG、Precision等指标来评估他们的表现。线下模型经过训练和评估后,如果在测试集有比较明显的提高,会将其上线进行线上AB测试。同时,我们也有多种维度的报表对模型进行数据上的支持。Ranking的主要职责如下:- 获取所有列表实体进行预测所需特征。- 将特征交给预测模块进行预测。- 对所有列表实体按照预测值进行排序。<a name="08058dcc"></a>### 数据采集- 人工标注 ground truth从搜索日志中随机选取一部分Query,让受过专业训练的数据评估员对”Query-Url对”给出相关性判断。常见的是5档的评分:(0:差、1:一般、2:好、3:优秀、4:完美)。以此作为训练数据。人工标注是标注者的主观判断,会受标注者背景知识等因素的影响。- 日志挖掘:当搜索引擎搭建起来之后用户的点击数据就变得非常好使,用户点击记录是可以当做机器学习方法训练数据的一个替代品,比如用户发出一个查询,搜索引擎返回搜索结果,用户会点击其中某些网页,可以假设用户点击的网页是和用户查询更加相关的页面。点击数据隐式反映了同Query下搜索结果之间相关性的相对好坏。在搜索结果中,高位置的结果被点击的概率会大于低位置的结果,这叫做”点击偏见”(Click Bias)。但采取以上的方式,就绕过了这个问题。因为我们只记录发生了”点击倒置”的高低位结果,使用这样的”偏好对”作为训练数据。但是日志抽取也存在问题:> 1. 用户总是习惯于从上到下浏览搜索结果> 1. 用户点击有比较大的噪声> 1. 一般头查询(head query)才存在用户点击**在实际场景中,**- **我们使用搜索积累的大量用户行为数据(如点击、点赞等), 这些行为数据可以作为弱监督训练数据。**使用到的用户行为日志表如下:- 输入日志(input表)详细记录了用户每次的输入,用于和点击/转化数据做联合分析;- 推荐日志(output表)详细打印了每次请求的参数信息和返回信息,如userid、输入的问题、请求时间、第几页、返回的搜索结果及对应的顺序位置;- 点击日志(click表)详细记录了每次点击行为(点击item列表及其对应的参数信息);- 我们把query与搜索结果的**相关性标签分为三档,即弱相关,相关与不相关**。- 在query的选择上,通过对近六个月的query进行统计挖掘<a name="710e4164"></a>### [数据去噪](https://blog.csdn.net/v_july_v/article/details/81319999)- 数据清洗- 考虑哪些信息对于模型结果是有效的,去掉脏数据- 补齐缺省值(中位数补齐、平均数补齐)- **样本去噪**- 无意义单字Query过滤。由于单字Query表达的语义通常不完整,用户点击行为也比较随机,这部分数据如果用于训练会影响最终效果。我们去除了包含无意义单字Query的全部样本。- 正样本(点击label=1,点赞label=2),若quey=doc情况下的doc未被点击,强制令其label=1;- 负样本中存在大量噪声数据,需要针对语料补充对应的过滤规则来过滤数据;- 数据采样- 一般来说,负样本远远多于正样本,导致样本不均衡。分类问题中样本不均衡,会导致模型整体偏向样本多的那个类别,导致其他类别不准确。解决方法主要有: 上采样、随机负采样、收集更多数据、数据增强EDA、修改损失函数(如** focal loss**)<a name="b2de4c49"></a>### [特征工程★](https://blog.csdn.net/v_july_v/article/details/81319999)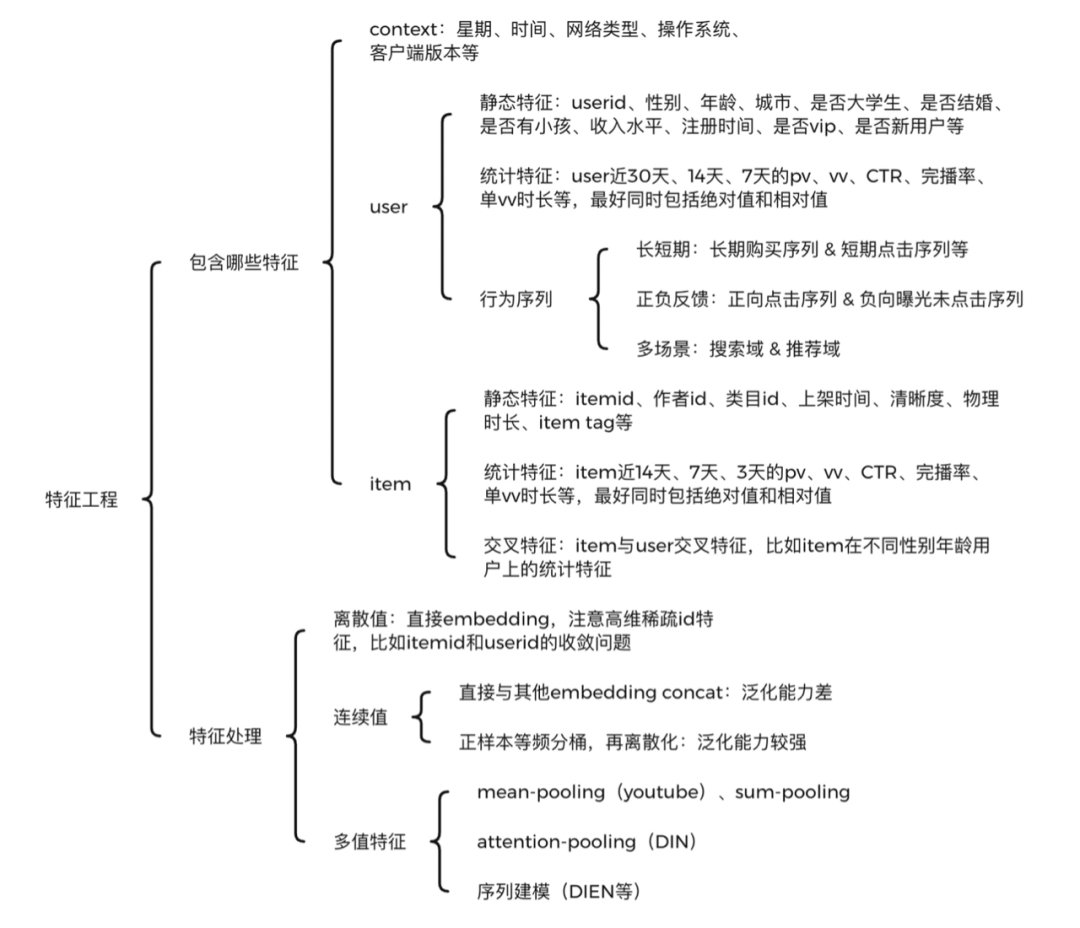**(一)主要有哪些特征**<br /><br />**精排是特征的艺术** ,虽然特征工程远远没有深度模型那么fancy,但在实际业务中,基于特征工程优化,比基于模型更稳定可靠,且效果往往不比优化模型低。特征工程一定要结合业务理解,在具体业务场景上,想象自己就是一个实际用户,会有哪些特征对你是否点击、是否转化有比较大的影响。一般来说,可以枚举如下特征:- **context特征** :如星期、时间、网络类型、操作系统、客户端版本等。- **user特征** ,也就是常说的用户画像,可以共享其他兄弟APP或者同一APP不同场景内的,用户各个维度的特征,主要包括**三部分** :- 静态特征:userid、性别、年龄、城市、职业、收入水平、是否大学生、是否结婚、是否有小孩、注册时间、是否vip、是否新用户等。静态特征一般区分度还是挺大的,比如不同性别、年龄的人,兴趣会差异很大。再比如是否有小孩,会直接决定母婴类目商品是否有兴趣。- 统计特征:比如user近30天、14天、7天的pv、vv、CTR、完播率、单vv时长等,最好同时包括绝对值和相对值。毕竟2次曝光1次点击,和200次曝光100次点击,CTR虽然相同,但其置信度天差地别。统计特征大多数都是后验特征,对模型predict帮助很大。统计特征一定要注意数据穿越问题,构造特征时千万不要把当天的统计数据也计算进去了。- 行为序列特征:这一块目前研究很火,也是精排模型提升的关键。可以构建用户短期点击序列和长期购买序列,也可以构建用户正反馈点击购买序列和负反馈曝光未点击序列。序列长度目前是一个痛点,序列过长时,Transformer等模型计算量可能很大,导致模型RT和P99等指标扛不住,出现大量超时。- **item特征** ,这一块不像用户画像容易兄弟APP共享,不同APP可能itemid等重要特征不能对齐,导致无法领域迁移。主要有如下特征:- 静态特征:如itemid、作者id、类目id、上架时间、清晰度、物理时长、item tag等。这些特征一般由机器识别、人工打标、用户填写运营审核等方式产出,十分重要。- 统计特征:如item近14天、7天、3天的pv、vv、CTR、完播率、单vv时长等,最好同时包括绝对值和相对值。跟user侧统计特征一样,要注意数据穿越问题。- 交叉特征:item与user交叉特征,比如item在不同性别年龄用户上的统计特征。虽然模型可以实现自动特征交叉,但是否交叉得好就要另说了。手工构造关键的交叉特征,还是很有意义的。**(二)怎么处理特征**特征的处理主要有如下几种情况:- **离散值**:比如“一天中哪个时间段”,直接embedding,注意高维稀疏id特征,比如one-hot编码- **连续值**:比如“页浏览时长”,主要有两种方式:- 直接与其他embedding concat:操作简单,但泛化能力差。- 正样本等频分桶,再离散化:泛化能力较强,是目前通用的解决方案。- **多值特征**:最典型的就是用户行为序列,主要方法有:- mean-pooling(youtube)、sum-pooling:将行为序列中item特征,逐个进行mean-pooling或者sum-pooling,比如youtube的论文。这个方法十分粗糙,完全没有考虑序列中不同item对当前的打分,以及行为的时序转化关系。- att-pooling:将行为序列中各item,与待打分target item,进行attention计算再平均,也就是加权平均,比如DIN。这个方法考虑了item的重要程度,也支持引入item的重要side info,通过引入item index,其实也可以带有一定的时序信息,可以作为序列建模的baseline。- 序列建模:将行为序列中各item,通过GRU等RNN模型,进行建模,取出最后一个位置的输出即可,比如DIEN。此方法考虑了用户行为的时序关系和兴趣迁移,目前基本都使用Transformer来进行时序建模,可以缓解反向传播梯度弥散、长序列建模能力差、串行耗时高等问题。- 文本型- 词袋模型(映射成稀疏向量)- Jaccard、Levenshtein、Simhash、TF-idf、Bm25- 幅度调整:提高梯度下降法的收敛速度- 归一化:`sklearn.preprocessing.MinMaxScaler` 把数据幅度调整到[0,1]范围内- 标准化:`sklearn.preprocessing.scale` 处理后的数据符合标准正态分布,即均值为0,标准差为1- **树形模型不需要特征归一化也不必担心缺失值,因为它们不关心变量的值,而是关心变量的分布和变量之间的条件概率,如决策树、随机森林!**在实际场景下,我们收集了如下几类特征:- 文档组成- query- primary question- similar question- answer- 特征分类- 交叉特征<br />主要是搜索的相关性特征,即计算用户Query和候选Doc两者之间相关度![参考]()- BM25相似度- TF-IDF相似度- ES返回的Score- String Cosine相似度- Embedding相似度(基于Glove、Doc2vec、BERT得到Query和Doc的表示向量,然后计算余弦相似度.)- 编辑距离、词共现- query关键词出现次数及比例- jaccard相似度- Query-Doc点击次数和点击率- 单边特征- [query词权重](https://mp.weixin.qq.com/s?__biz=MzU1NTMyOTI4Mw==&mid=2247508936&idx=2&sn=78be7e9852a78ddf0da07198b6c7978b&chksm=fbd711a4cca098b245bcdba6932d42927a95ebf01fb949f3e4dbf8d74efc63e6c619357fc702&mpshare=1&scene=1&srcid=1013bKeTJiZPMKWHeGyO8il8&sharer_sharetime=1602575301868&sharer_shareid=1539cddeb9761bf9ab11f818eaf32ccd&key=0e194573360c8aa2a4aac7e900023ab49de9e41da0eed6dfefe4c448b54365646757fa4353f3c564de211b8858ac1b7a4aeebdad0b447f8cec6eacb8bb0bb911a6b67814994175cb4fda6c6602f8c6cd7a81c45a1632431fba29863fe20ac7c9af9fd488973d9c3feed2ba51cf484002e291a847faaf3be2e21a76dc31b8e830&ascene=1&uin=MjM2MDA1NjcyMQ%3D%3D&devicetype=Windows+10+x64&version=6300002f&lang=zh_CN&exportkey=A8ykpIlyUpzN8fKs63fFFqM%3D&pass_ticket=Ci2XyVC7HEwQ1U4ddZ%2BTa0dDdVzykUszBehfKZob3hleSuYqaB%2Bj56ke%2FGHlx9Pa&wx_header=0)- query长度- Doc长度- Doc时间戳(问题的新鲜度)- Doc更新时间- Doc的具体信息,包括xxx- ID类特征(docID、itemID、answerID、baseCode、botCode、projectCode)- ~~点击率~~- ~~来源source、点赞数、点击反馈、高亮字数~~- 全局特征- 召回阶段doc的全局位置特征SearchOrder- 召回阶段doc所在的当前页面- 请求时间段<a name="9140604a"></a>### [特征筛选](https://blog.csdn.net/v_july_v/article/details/81319999)各种特征处理之后会产生很多特征,他们之间会存在如下问题:- 冗余:部分特征的相关度太高了,消耗计算性能- 噪声:部分特征是对预测结果有**负影响**针对这两个问题,咱们便得做下特征选择 & 降维:- 特征选择是指踢掉原本特征里和结果预测关系不大的- SVD或者PCA确实也能解决一定的高维度问题从众多特征中挑选出少许有用特征。与学习目标不相关的特征和冗余特征需要被剔除,如果计算资源不足或者对模型的复杂性有限制的话,还需要选择丢弃一些不重要的特征。**特征选择方法常用的有以下几种:****1 过滤型**评估单个特征和结果值之间的相关程度,排序留下Top相关的特征部分。而计算相关程度可以用Pearson相关系数、互信息、距离相关度来计算。这种方法的缺点是:没有考虑到特征之间的关联作用,可能把有用的关联特征误踢掉。```pythonfrom sklearn.datasets import load_irisfrom sklearn.feature_selection import SelectKBestfrom sklearn.feature_selection import chi2iris = load_iris()X,y = iris.data, iris.targetX. shape# (150, 4)X_new = SelectKBest(chi2, k=2).fit_transform(X,y)X_new.shape# (150, 2)
2 包裹型
包裹型是指把特征选择看做一个特征子集搜索问题,筛选各种特征子集,用模型评估效果。典型的包裹型算法为 “递归特征删除算法”(recursive feature elimination algorithm)。
比如用逻辑回归,怎么做这个事情呢?
- 用全量特征跑一个模型
- 根据线性模型的系数(体现相关性),删掉5-10%的弱特征,观察准确率/auc的变化
- 逐步进行,直至准确率/auc出现大的下滑停止
3 嵌入型
嵌入型特征选择是指根据模型来分析特征的重要性,比如决策树的featureimportances属性,返回的重要性是按照决策树种被用来分割后带来的增益(gain)总和进行返回。
gbm.feature_importance()
训练样本构建
首先,需要将数据格式处理成 libsvm格式,作为 LightGBM 的输入:
- 每一行的行首是该样本的因变量y,是我们要预测的目标值,比如{1, -1};
- y后面跟着的是各个自变量,即各维度的特征。但是注意这些自变量不是直接排在因变量后面,而是以 “索引: 取值” 的方式依次排在后面——索引就是第几个自变量;依次类推。如果样本中某个自变量的取值为0,那么该自变量的可以不出现,例如,如果第20个自变量取值为0,那么可以采用“19:XXXX 21:XXXX”形式,跳过“20:0”,这样做可以减少内存的使用,并提高做矩阵内积时的运算速度。
模型训练与评估

我们选择 IR 领域是最先进的LambdaMART模型,基于 lightGBM 的 GBDT 树模型进行训练,方便dump和load模型,采用 lambdarank 损失来进行训练,以 NDCG 指标作为优化方向。
- GBDT(Gradient Boosting Decision Tree) 又叫 MART(Multiple Additive Regression Tree),一种迭代的决策树算法
- LambdaRank pairwise loss 引入RankNet的Lambda梯度,直接用
乘以
得到 LambdaRank 的 Lambda
%7D%5Cright)%20%5Ccdot%5Cleft%7C%5CDelta%20Z%7Bi%20j%7D%5Cright%7C#card=math&code=C%7Bi%20j%7D%3D%5Clog%20%5Cleft%281%2Be%5E%7B-%5Csigma%5Cleft%28s%7Bi%7D-s%7Bj%7D%5Cright%29%7D%5Cright%29%20%5Ccdot%5Cleft%7C%5CDelta%20Z_%7Bi%20j%7D%5Cright%7C&id=E0y60)
使用到的一些参考资源:
- LambdaRank,基于xgboost实现,参考:https://github.com/dmlc/xgboost/tree/master/demo/rank
- LambdaMART,基于LightGBM实现,参考:https://github.com/jiangnanboy/learning_to_rank
- Wide&Deep基于TensorFlow实现,参考:https://github.com/tensorflow/ranking
Lightgbm代码示例
Xgboost代码示例
tensorflow_ranking代码示例
- Implement Listwise LTR using
[tensorflow](https://everdark.github.io/k9/notebooks/ml/learning_to_rank/learning_to_rank.html)
模型预测
preds_test = gbm.predict(X, num_iteration=best_iteration, num_threads=1)# 根据group切分预测概率并排序rank = ut.Sort.resort(preds_test)
模型分发
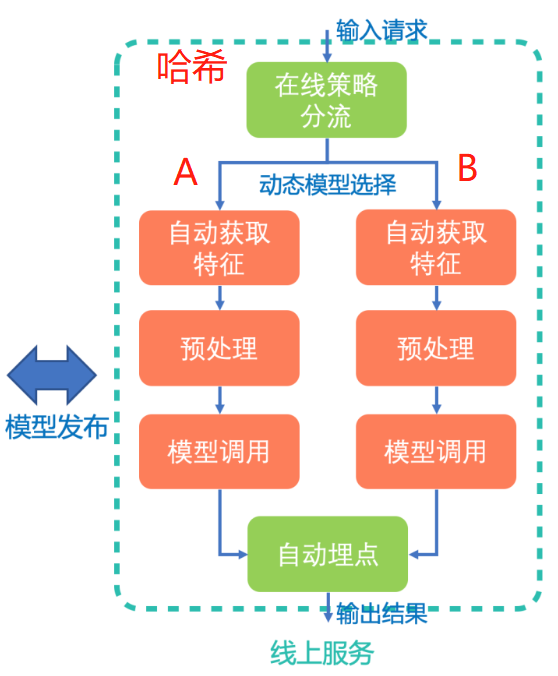
模型分发的目标是把在线流量分配给不同的实验模型,具体而言要实现三个功能:
- 为模型迭代提供在线流量,负责线上效果收集、验证等。
- A/B测试,确保不同模型之间流量的稳定、独立和互斥、确保效果归属唯一。
- 确保与其他层的实验流量的正交性。
采用如下步骤将流量分配到具体模型上面去:
- 把所有流量分成N个桶。
- 每个具体的流量Hash到某个桶里面去。
- 给每个模型一定的配额,也就是每个策略模型占据对应比例的流量桶。
- 所有策略模型流量配额总和为100%。
- 当流量和模型落到同一个桶的时候,该模型拥有该流量。
拓展:LTR模型详细介绍
模型分类
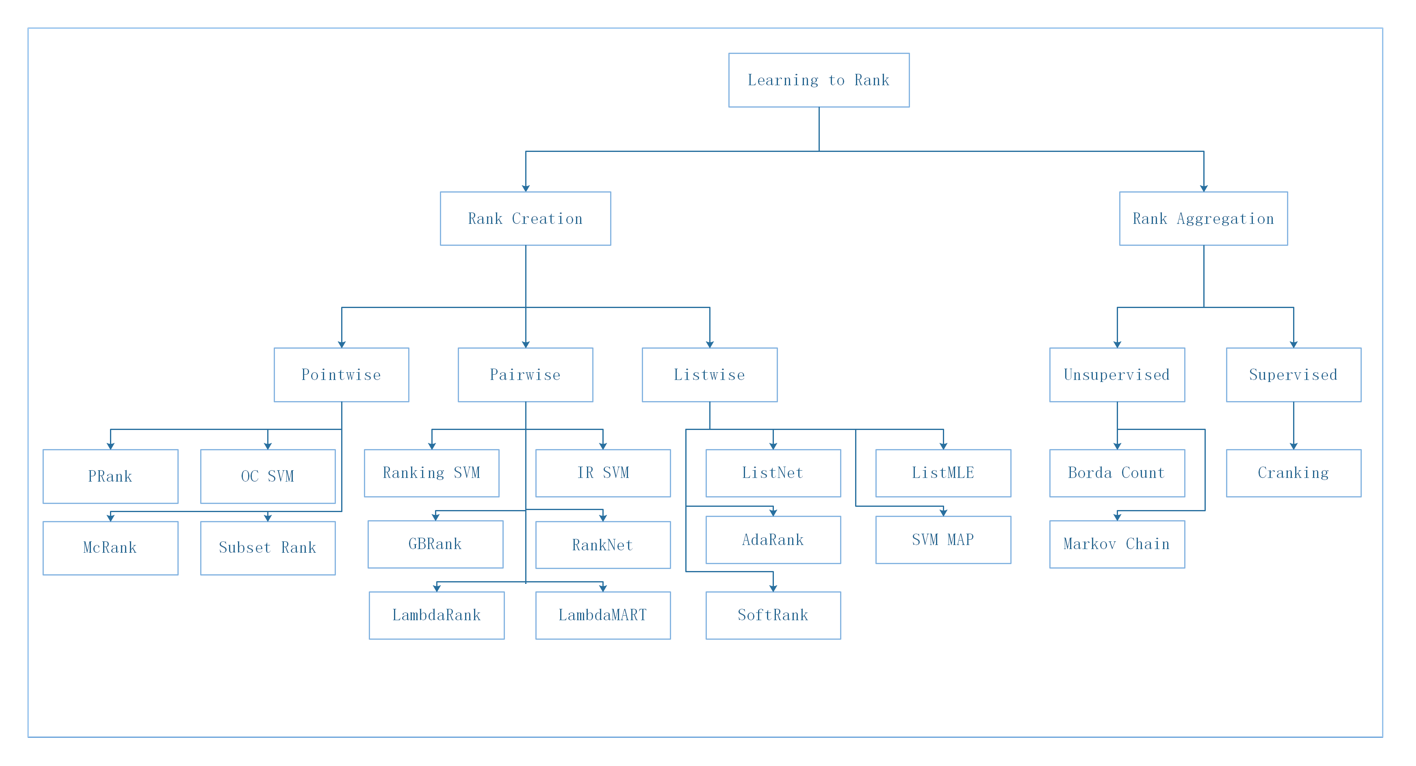
已发表并广泛接受的重排或者 LTR 工作分为这么几类(参考):
Point-wise 模型:和经典的 CTR 模型基本结构类似,如 DNN [8], WDL [9] 和 DeepFM [10]。和排序相比优势主要在于实时更新的模型、特征和调控权重。LTR 对于调控权重的能力还是基于单点的,没有考虑到商品之间互相的影响,因此并不能保证整个序列收益最优。
Pair-wise 模型:通过 pair-wise 损失函数来比较商品对之间的相对关系。具体来说,RankSVM [12], GBRank [13] 和 RankNet [2] 分别使用了 SVM、GBT 和 DNN。但是,pair-wise 模型忽略了列表的全局信息,而且极大地增加了模型训练和预估的复杂度。
List-wise 模型:建模商品序列的整体信息和对比信息,并通过 list-wise 损失函数来比较序列商品之间的关系。LambdaMart [14]、MIDNN [3]、DLCM[6]、PRM [5] 和 SetRank [4] 分别通过 GBT、DNN、RNN、Self-attention 和 Induced self-attention 来提取这些信息。但是由于最终还是通过贪婪策略进行排序,还是不能真正做到考虑到排列特异性的上下文感知。随着工程能力的升级,输入序列的信息和对比关系也可以在排序阶段中提取出来。
Pointwise Ranker
首先介绍Pointwise排序模型,这种模型直接对标注好的pointwise数据,学习#card=math&code=P%28y%7C%5Cboldsymbol%7Bx%7D%29&id=JhmLA)或直接回归预测
。从早期的线性模型LR,到引入自动二阶交叉特征的FM和FFM,到非线性树模型GBDT和GBDT+LR,到最近全面迁移至大规模深度学习排序模型。
LR
LR(logistics regression),是CTR预估模型的最基本的模型,也是工业界最喜爱使用的方案,排序模型化的首选。实际优化过程中,会给样本添加不同权重,例如根据反馈的类型点击、浏览、收藏、下单、支付等,依次提高权重,优化如下带权重的损失:
%3D-%5Cfrac%7B1%7D%7Bm%7D%5Csum%7Bi%3D1%7D%5Em%20w_i%20%5Ccdot%20%5CBig(%20y_i%20log(%5Csigma%5Ctheta(%5Cboldsymbol%7Bx%7Di))%2B(1-y_i)log(1-%5Csigma%5Ctheta(%5Cboldsymbol%7Bx%7Di))%5CBig)%0A#card=math&code=J%28%5Ctheta%29%3D-%5Cfrac%7B1%7D%7Bm%7D%5Csum%7Bi%3D1%7D%5Em%20wi%20%5Ccdot%20%5CBig%28%20y_i%20log%28%5Csigma%5Ctheta%28%5Cboldsymbol%7Bx%7Di%29%29%2B%281-y_i%29log%281-%5Csigma%5Ctheta%28%5Cboldsymbol%7Bx%7D_i%29%29%5CBig%29%0A&id=oAI8J)
其中,是样本的权重,
是样本的标签。
%3D%5Cfrac%7B1%7D%7B1%2Be%5E%7B-(%5Cboldsymbol%7B%5Ctheta%7D%5Ccdot%20%5Cboldsymbol%7Bx%7D%2B%20%5Cboldsymbol%7Bb%7D)%7D%7D#card=math&code=%5Csigma_%7B%5Ctheta%7D%28%5Cboldsymbol%7Bx%7D_i%29%3D%5Cfrac%7B1%7D%7B1%2Be%5E%7B-%28%5Cboldsymbol%7B%5Ctheta%7D%5Ccdot%20%5Cboldsymbol%7Bx%7D%2B%20%5Cboldsymbol%7Bb%7D%29%7D%7D&id=OhjKQ)。
模型优点是可解释性强。通常而言,良好的解释性是工业界应用实践比较注重的一个指标,它意味着更好的可控性,同时也能指导工程师去分析问题优化模型。但是LR假设各特征间是相互独立的,忽略了特征间的交互关系,因此需要做大量的特征工程。同时LR对非线性的拟合能力较差,限制了模型的性能上限。通常LR可以作为Baseline版本。
GBDT
GBDT (梯度提升决策树) 又叫 MART(Multiple Additive Regression Tree),是一种表达能力比较强的非线性模型。GBDT是基于Boosting 思想的ensemble模型,由多棵决策树组成,具有以下优点:
- 处理稠密连续值特征(特征的量纲、取值范围无关,故可以不用做归一化)
- 学习模型可以输出特征的相对重要程度,可以作为一种特征选择的方法
- 对数据字段缺失不敏感
- 根据熵增益自动进行特征转换、特征组合、特征选择和离散化,挖掘高维的组合特征,省去了人工转换的过程,并且支持了多个特征的Interaction
GBDT的主要缺陷是依赖连续型的统计特征,对于高维度稀疏特征、时间序列特征不能很好的处理。如果我们需要使用GBDT的话,则需要将很多特征统计成连续值特征(或者embedding),这里可能需要耗费比较多的时间。鉴于此Facebook提出了一种GBDT+LR的方案。
GBDT+LR
GBDT+LR方法是Facebook2014年提出在论文Practical Lessons from Predicting Clicks on Ads at Facebook提出的点击率预估方案。其动机主要是因为LR模型中的特征组合很关键, 但又无法直接通过特征笛卡尔积解决,只能依靠人工经验,耗时耗力同时并不一定会带来效果提升。如何自动发现有效的特征、特征组合,弥补人工经验不足,缩短LR特征实验周期,是亟需解决的问题。
GBDT+LR的核心思想是利用GBDT训练好的多棵树,某个样本从根节点开始遍历,可以落入到不同树的不同叶子节点中,将叶子节点的编号作为GBDT提取到的高阶特征,该特征将作为LR模型的输入。原论文中的模型结构如下:
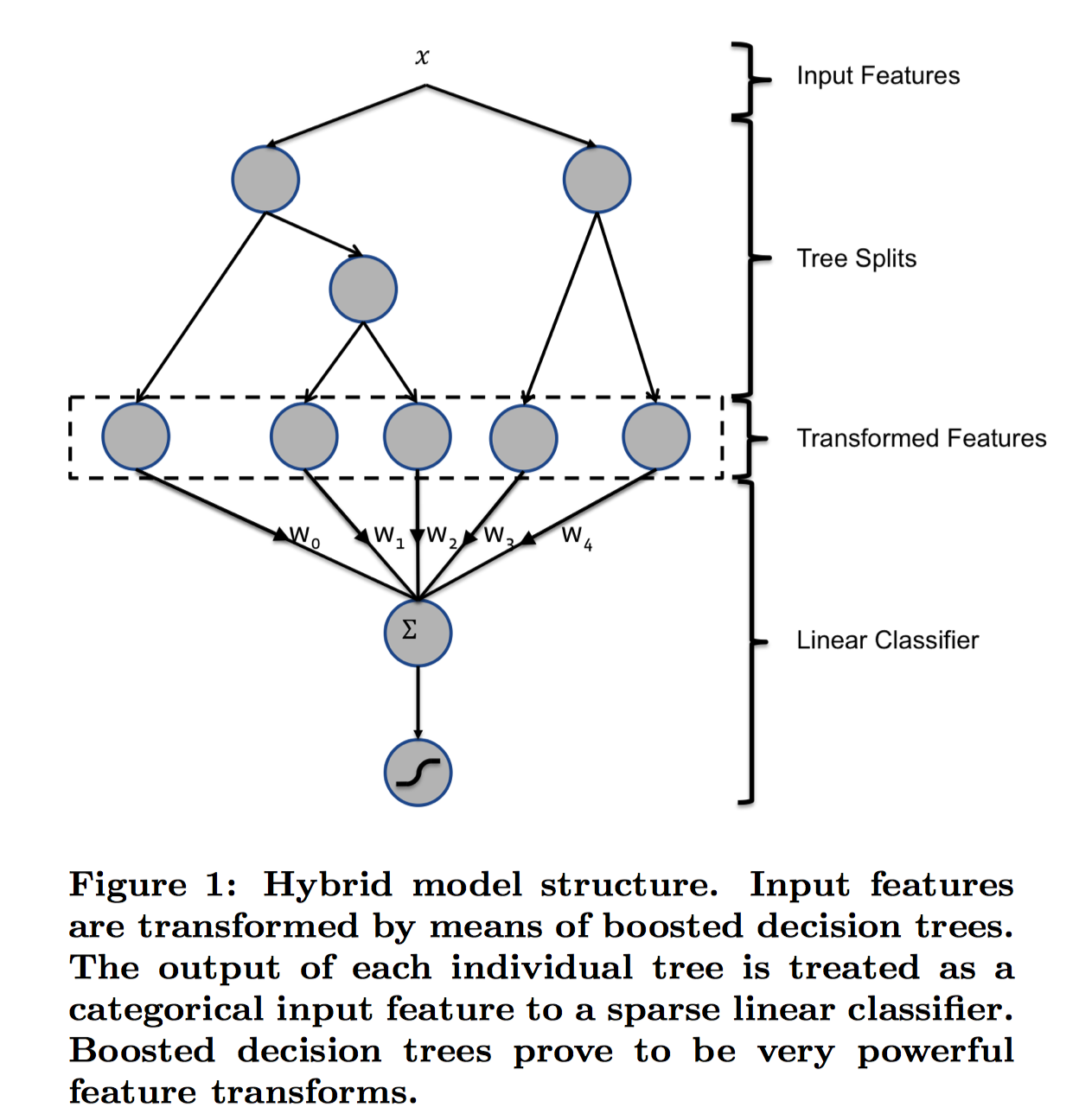
图中是一个样本,
两个子节点对应两棵子树Tree1、Tree2为通过GBDT模型学出来的两颗树。遍历两棵树后,
样本分别落到两棵树的不同叶子节点上,每个叶子节点对应提取到的一个特征,那么通过遍历树,就得到了该样本对应的所有特征。由于树的每条路径,是通过最小化均方差等方法最终分割出来的有区分性路径,根据该路径得到的特征、特征组合都相对有区分性,效果理论上不会亚于人工经验的处理方式。 最后,将提取到的叶子节点特征作为LR的输入。
实验结果表明:GBDT-LR 比单独的 GBDT 模型,或者单独的 LR 模型都要好。另外,GBDT树模型可以使用目前主流的XGBoost或者LightGBM替换,这两个模型性能更好,速度更快。
GBDT+FM
GBDT+LR排序模型中输入特征维度为几百维,都是稠密的通用特征。这种特征的泛化能力良好,但是记忆能力比较差,所以需要增加高维的(百万维以上)内容特征来增强推荐的记忆能力,包括物品ID,标签,主题等特征。GBDT不支持高维稀疏特征,如果将高维特征加到LR中,一方面需要人工组合高维特征,另一方面模型维度和计算复杂度会是#card=math&code=O%28n%5E2%29&id=iRlr5)级别的增长。所以设计了GBDT+FM的模型如图所示,采用Factorization Machines模型替换LR。

该模型既支持稠密特征,又支持稀疏特征。其中,稠密特征通过GBDT转换为高阶特征(叶子节点编号),并和原始低阶稀疏特征作为FM模型的输入进行训练和预测,并支持特征组合。且根据上述,FM模型的复杂度降低到#card=math&code=O%28n%29&id=wVvLx)(忽略隐向量维度常数)。
DNN 深度模型
进入深度模型时代后,精排模型发展更为迅猛,借用王喆老师的一张图,如下: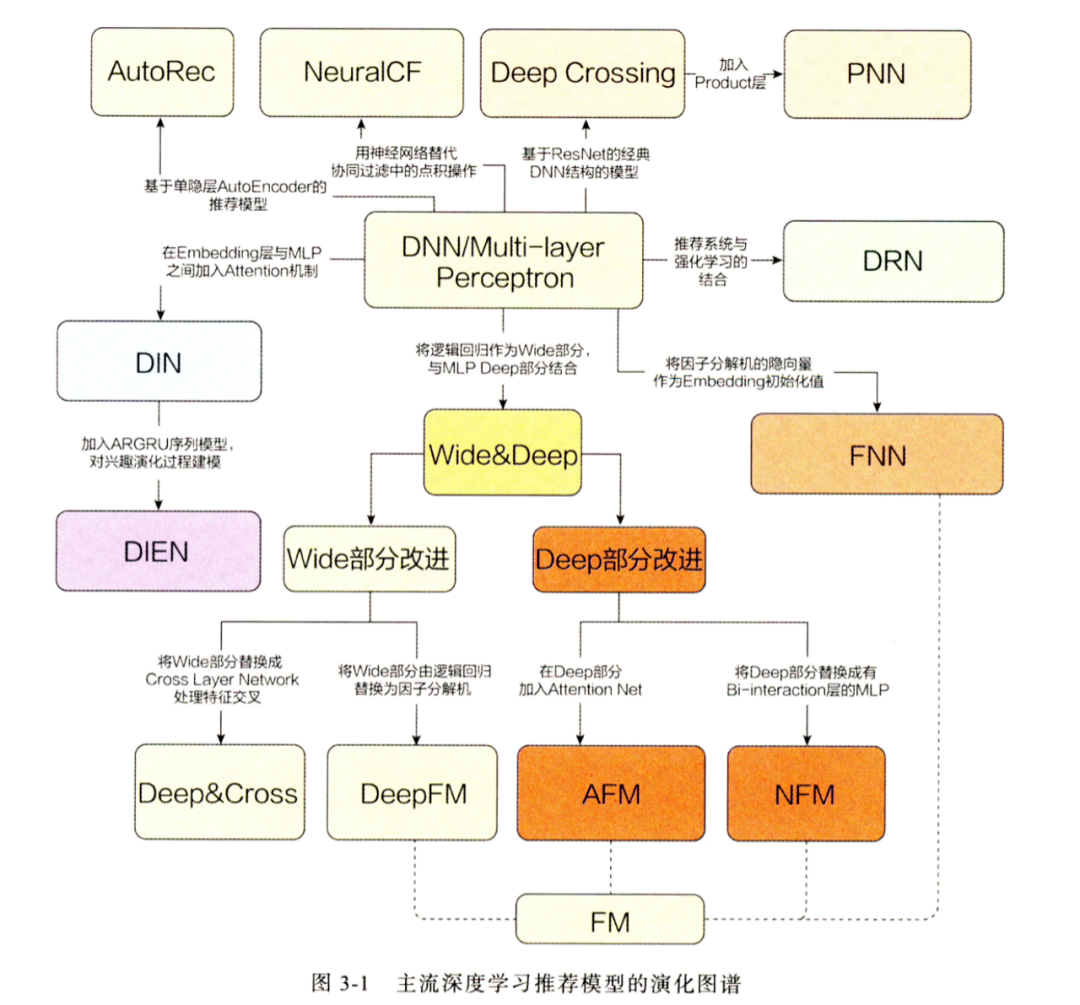
YouTube 2016发表了一篇基于神经网络的推荐算法Deep Neural Networks for YouTube Recommendations。文中使用神经网络分别构建召回模型和排序模型。简要介绍下召回模型。召回模型使用基于DNN的超大规模多分类思想,即在时刻,为用户
(上下文信息
)在视频库
中精准的预测出用户想要观看的视频为
的概率,用数学公式表达如下:
%3D%5Cfrac%7Be%5E%7Bvi%5ET%20u%7D%7D%7B%5Csum%7Bj%20%5Cin%20V%7D%20e%5E%7Bvj%5ETu%7D%7D%0A#card=math&code=p%28w_t%3Di%7CU%2CC%29%3D%5Cfrac%7Be%5E%7Bv_i%5ET%20u%7D%7D%7B%5Csum%7Bj%20%5Cin%20V%7D%20e%5E%7Bv_j%5ETu%7D%7D%0A&id=J87RJ)
向量是信息的高维embedding,而向量
则是视频的embedding向量,通过u与v的点积大小来判断用户与对应视频的匹配程度。所以DNN的目标就是在用户信息和上下文信息为输入条件下学习视频的embedding向量
以及用户的embdedding向量
。

分为离线计算和在线服务两个部分。离线计算的时候,通过embedding提取用户的不同特征(历史观影序列、搜索词),同类型特征先average,然后再将不同类型特征concat起来,作为MLP的输入,最后一层隐藏层的输出作为用户的embedding向量,再和视频的embedding向量点乘,并用于预测该视频概率。(输出层神经元由所有视频构成,最后一层隐藏层和该视频对应的输出层某个神经元相连接的权重向量就是该视频的embedding)。在线服务的时候,利用学习到的用户embedding和视频embedding,并借助近似近邻搜索,求出TopN候选结果(这里的问题是最后使用的video vectors如何构建的问题,是直接使用最后全连接层的权重还是使用最底下embedded video watches中的各视频的embedding。这个问题已有大神讨论过,见关于’Deep Neural Networks for YouTube Recommendations’的一些思考和实现)
排序模型和上述几乎一样,只不过最后一层输出不是softmax多分类问题,而是logistic regression二分类问题,并且输入层使用了更多的稀疏特征和稠密特征。之所以在候选阶段使用softmax,是因为候选阶段要保证多样性等,因此面向的是全量片库,使用softmax更合理。而在排序阶段,需要利用实际展示数据(impression data)、用户反馈行为数据来对候选阶段的结果进行校准,由于召回阶段已经过滤了大量的无关物品,因此排序阶段可以进一步提取描述视频的特征、用户和物品关系的特征等。
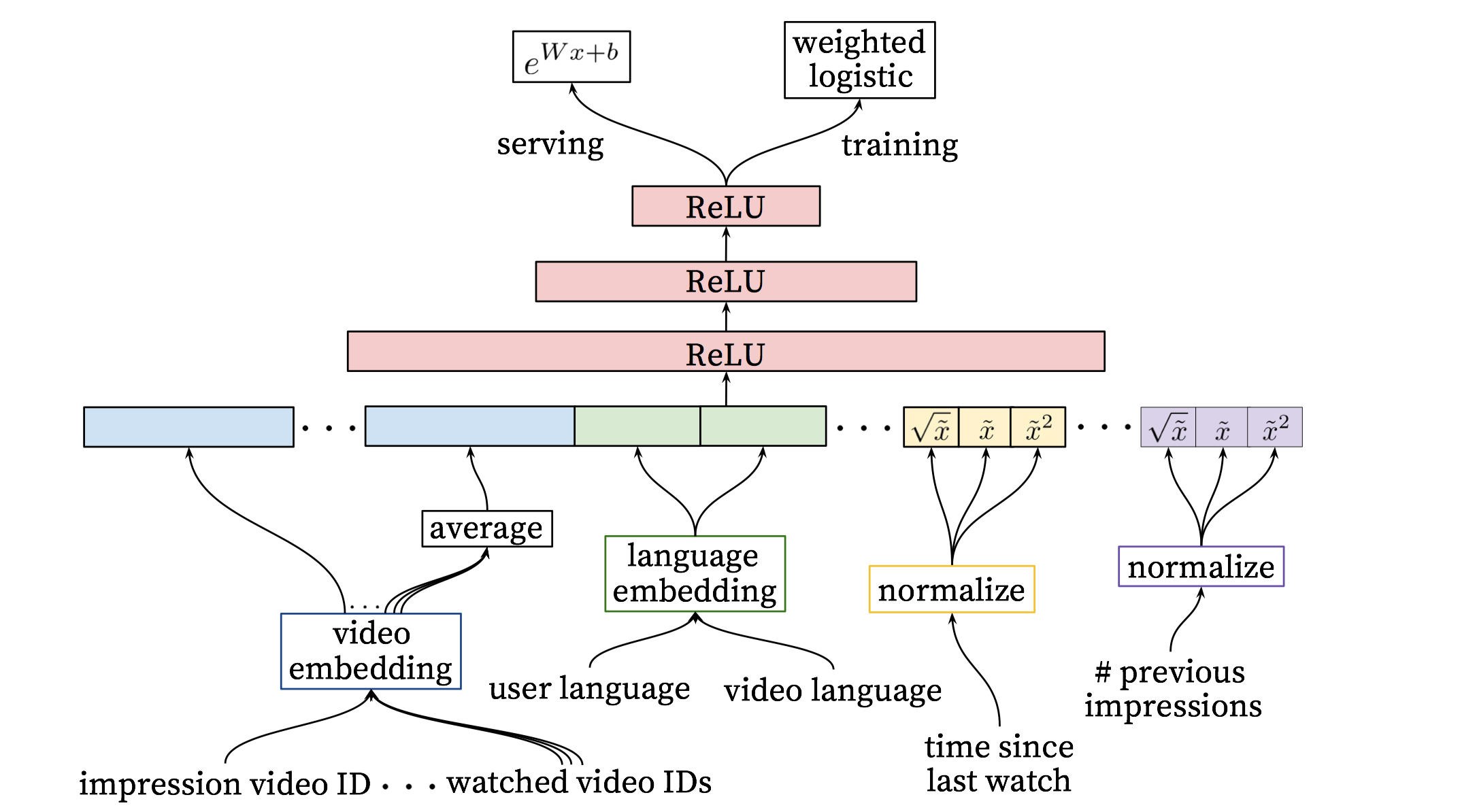
同样分为训练部分和服务部分。训练时,提取了更多关于视频、用户、上下文的特征,其中,稀疏特征通过embedding方式传入,稠密特征通过归一化、幂率变换等传入,最后使用加权的logistic regression来训练,权重使用观看时长表示,最大化#card=math&code=P%28y%7C%5Cboldsymbol%7Bx%7D%29&id=VB9sa)的概率。
训练好后,使用来计算得分并排序即可(不需要进行sigmoid操作,排序时二者等价)。
- Wide & Deep Learning
该模型是Google 2016论文 Wide & Deep Learning for Recommender Systems 提出的,用于Google Play应用中app的推荐。该模型结合了LR线性模型的记忆能力和DNN深度模型的泛化能力,即:广义线性模型表达能力不强,容易欠拟合;深度神经网络模型表达能力太强,容易过拟合。二者结合就能取得平衡。
宽度学习组件 linear model:LM 的输入主要是稀疏特征以及稀疏特征间转换后的交叉特征,能够实现记忆性,记忆性体现在从历史数据中直接提取特征的能力;
深度学习组件 neural network:NN 的输入包括了稠密特征以及稀疏特征,其中稀疏特征通过embedding方式转换成稠密特征,能够实现泛化性,泛化性体现在产生更一般、抽象的特征表示的能力。
我们希望在宽深度模型中的宽线性部分可以利用交叉特征去有效地记忆稀疏特征之间的相互作用,而在深层神经网络部分通过挖掘特征之间的相互作用,提升模型之间的泛化能力。下图是宽深度学习模型框架:
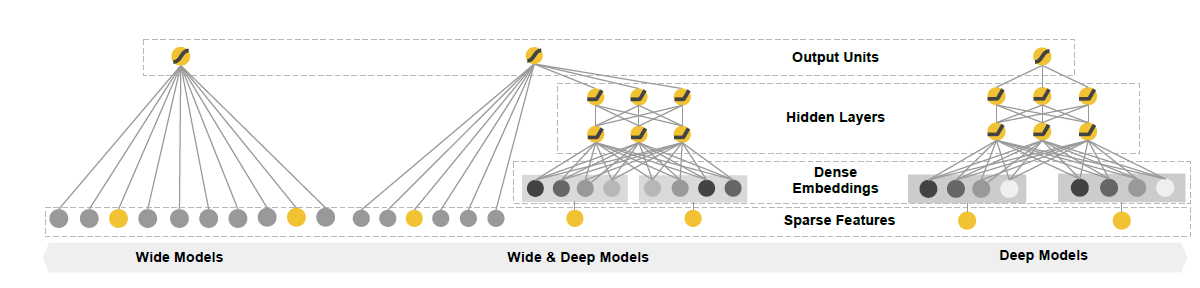
wide learning 形式化为:%5C%7D%20%2B%20b#card=math&code=y%3DW_%7B%5Ctext%7Bwide%7D%7D%5ET%20%5C%7B%5Cboldsymbol%7Bx%7D%2C%20%5Cphi%28%5Cboldsymbol%7Bx%7D%29%5C%7D%20%2B%20b&id=JXd6X),其中
是原始稀疏特征,
#card=math&code=%5Cphi%28%5Cboldsymbol%7Bx%7D%29&id=mXCVd)是手动精心设计的、变换后的稀疏特征,
%5C%7D#card=math&code=%5C%7B%5Cboldsymbol%7Bx%7D%2C%20%5Cphi%28%5Cboldsymbol%7Bx%7D%29%5C%7D&id=mAptu)表示特征拼接。
deep learning形式化为:,deep组件的输入包括连续值特征以及稀疏特征。其中稀疏特征通过embedding方式转换成稠密特征。sigmoid激活后:
%20%3D%20%5Csigma(W%5ET%7B%5Ctext%7Bwide%7D%7D%5C%7B%5Cboldsymbol%7Bx%7D%2C%5Cphi(%5Cboldsymbol%7Bx%7D)%5C%7D%20%2B%20W%5ET%7B%5Ctext%7Bdeep%7D%7Da%5E%7B(lf)%7D%2B%20bias)%0A#card=math&code=P%28%5Chat%7Br%7D%7Bui%7D%3D1%7Cx%29%20%3D%20%5Csigma%28W%5ET%7B%5Ctext%7Bwide%7D%7D%5C%7B%5Cboldsymbol%7Bx%7D%2C%5Cphi%28%5Cboldsymbol%7Bx%7D%29%5C%7D%20%2B%20W%5ET%7B%5Ctext%7Bdeep%7D%7Da%5E%7B%28l_f%29%7D%2B%20bias%29%0A&id=s07e6)
其中,表示正反馈行为,
#card=math&code=P%28%5Chat%7Br%7D_%7Bui%7D%3D1%7Cx%29&id=Qwqq2)是正反馈行为的概率。
- Deep FM(wide侧改进)
DeepFM(Deep Factorization Machine)是哈工大Guo博士在华为诺亚实验室实习期间,提出的一种深度学习方法,它基于Google的经典论文Wide&Deep基础上,通过将原论文的wide部分(LR部分)替换成FM,从而改进了原模型依然需要人工特征工程的缺点,得到一个end-to-end 的深度学习模型。

- DCN:Deep&Cross(wide侧改进)
上一小节讲到为了加强低阶特征的表达能力,将W&D中的LR线性部分替换成FM。FM的本质是增加了低纬特征间的二阶交叉能力,为了挖掘更高阶的特征交叉的价值提出了DCN (Deep &Cross Network)模型。

比较DCN与DeepFM的网络架构,可以发现本质区别是将DeepFM的FM结构替换为Cross Network结构。在输入侧,稀疏特征通过embedding层转化为稠密特征后,和连续特征concat起来,一起作为模型的输入。因此,输入层面只有embedding column+continuous column, 特征组合在网络结构中自动实现。上图右侧是常见的MLP深度网络,左侧是本文提出的交叉网络。下面看下什么是Cross Network? 以及Cross Network是如何实现高阶特征组合的?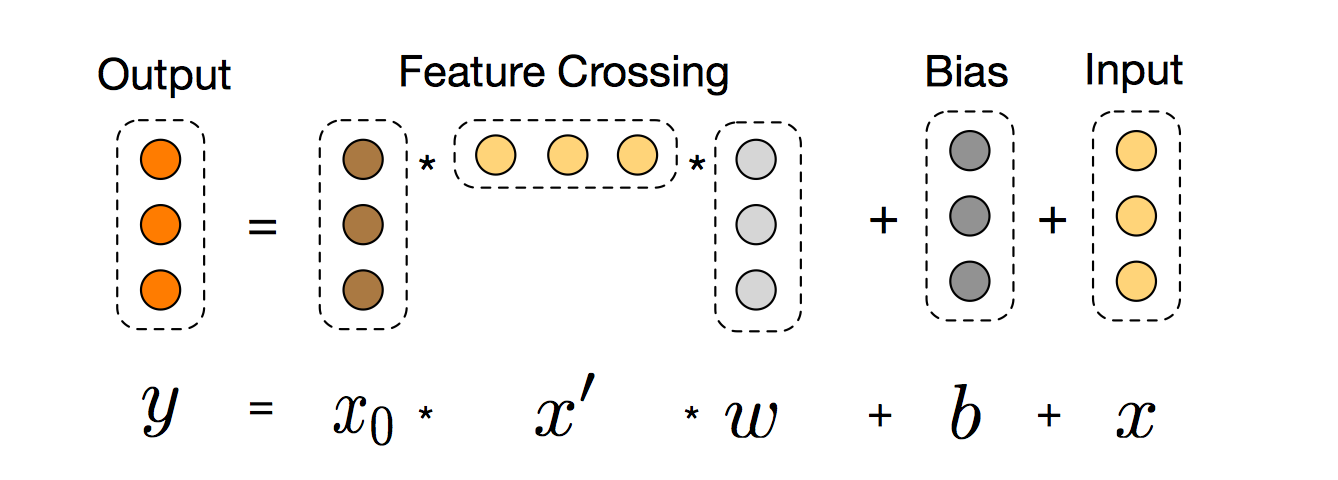
Cross Network整体看是一个递推结构:
%20%2B%20xl%0A#card=math&code=x%7Bl%2B1%7D%20%3D%20x_0%20x_l%5ETw_l%20%2B%20b_l%20%2B%20x_l%20%3D%20f%28x_l%2Cw_l%2Cb_l%29%20%2B%20x_l%0A&id=pq3PB)
首先, 为输入的特征(第一层输入),
为第 L 层的输入,
(
)和
(
)为第
层的参数矩阵。结合图可以看出Cross Network通过矩阵乘法实现特征的组合。每一层的特征都由其上一层的特征进行交叉组合,并把上一层的原始特征重新加回来。这样既能做特征组合,自动生成交叉组合特征,又能保留低阶原始特征,随着cross层的增加,是可以生成任意高阶的交叉组合特征(而DeepFM模型只有2阶的交叉组合特征)的,且在此过程中没有引入更多的参数(仅仅为
),有效控制了模型复杂度。
同时为了缓解网络性能”退化“的问题,还引入了残差的思想:
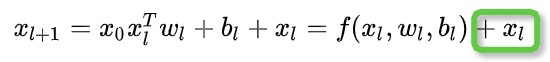
总结一下,DCN提出了一种新的交叉网络,在每个层上明确地应用特征交叉,能够有效地捕获有限度的有效特征的相互作用,学会高度非线性的相互作用,不需要人工特征工程或遍历搜索,并具有较低的计算成本。此外Cross Network可以看成是对FM的泛化,而FM则是Cross Network在阶数为2时的特例。
- NFM(deep侧改进)
NFM则对W&D的deep部分进行了改进,它在embedding层和DNN层之间,加入了特征交叉池化层。对两个长度相同的embedding向量,进行相同位置元素内积操作再求和,从而得到池化层输出。通过加入特征交叉池化层,来增强deep部分特征交叉能力。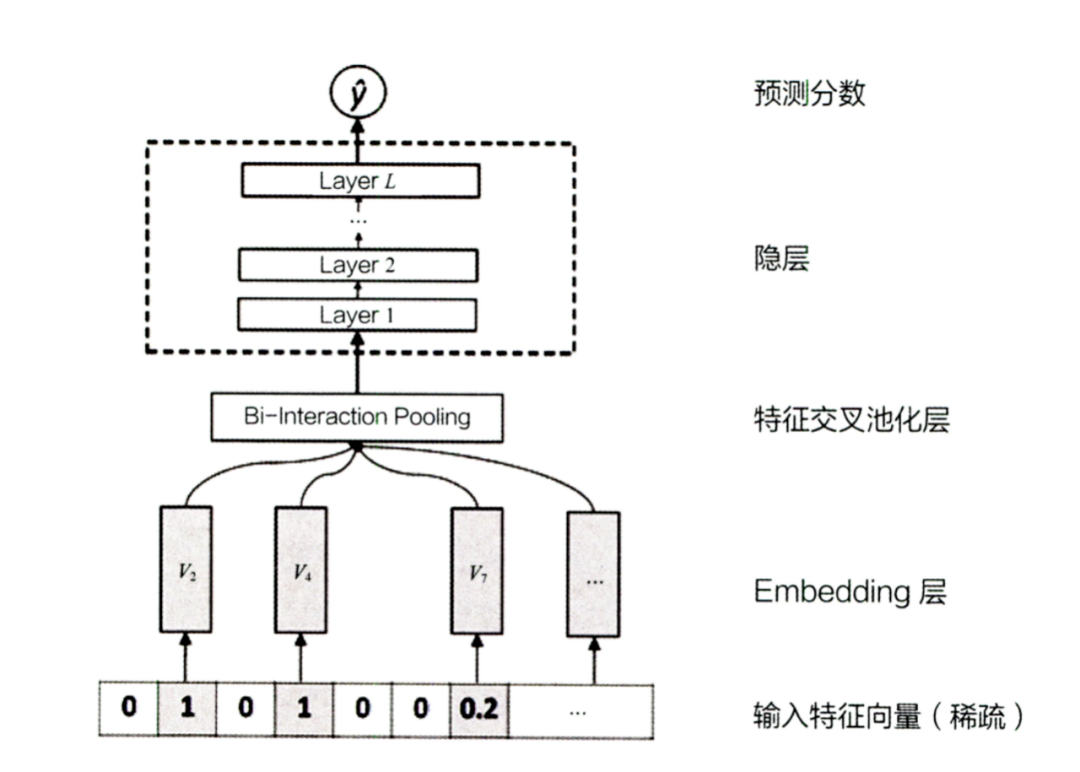
- xDeepFM(加入子分支)
xDeepFM则在 wide&deep 两个分支基础上,新引入了一个分支CIN,具体就先不展开了,后面文章详细分析。如下图所示,注意新增了一个子分支CIN。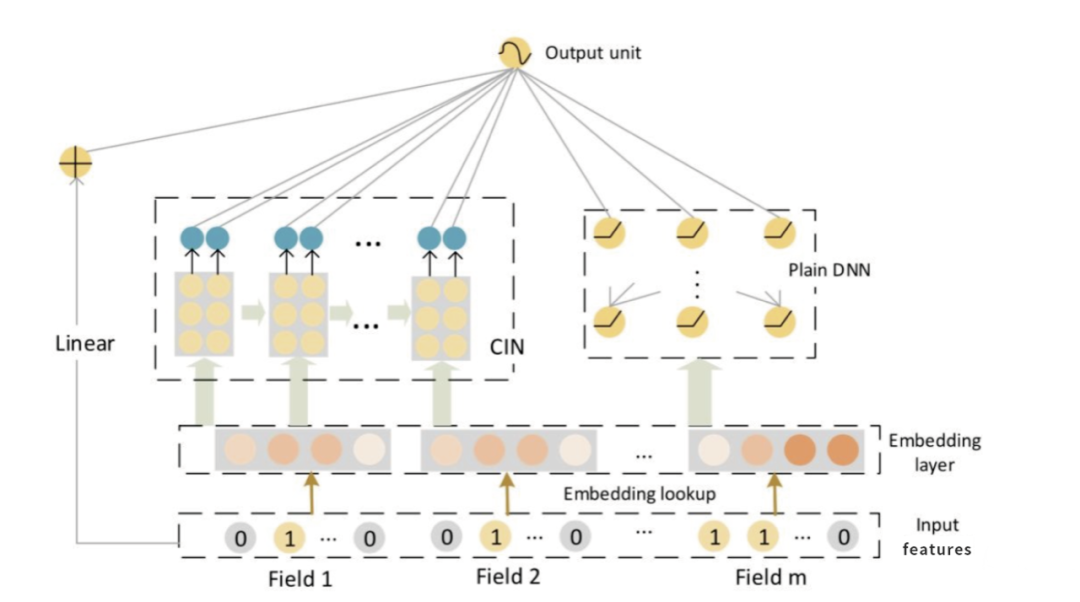
除此之外,attention和序列建模都是解决多值特征的pooling问题的,最常见的多值特征就是用户行为序列,也是目前模型提升的关键。也使得精排模型融入了序列建模机制,是一个比较大的改变。如:AFM、autoInt、FiBiNet、DIN等。
Pairwise Ranker
点级排序学习技术完全从单个物品的分类得分角度计算,没有考虑物品之间的顺序关系。而对级排序学习技术则偏重于对物品顺序关系是否合理进行判断,判断任意两个物品组成的物品对,是否满足顺序关系,即,item 1是否应该排在 item 2 前面(相比于item 2, 用户更偏好于item 1)。具体构造偏序对的方法见Basic一节。支持偏序对的模型也有很多,例如支持向量机、BPR、神经网络等。
然而,无论使用哪一种机器学习方法,最终目标都是判断对于目标用户,输入的物品对之间的顺序关系是否成立,从而最终完成物品的排序任务来得到推荐列表。
RankSVM
参考:https://www.cnblogs.com/bentuwuying/p/6683832.html
Ranking SVM 算法是通过在训练集构造样本有序数据对的方式将排序问题转化为应用支持向量机方法解决的分类问题,如下图所示。
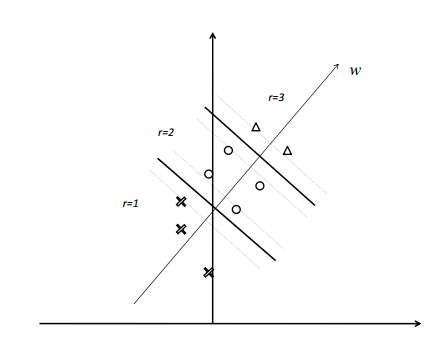
在SVM中,为实现软间隔最大化, 需要满足约束%20%3E%201-%20%5Cxii#card=math&code=y_i%28w%5ETx_i%20%2Bb%29%20%3E%201-%20%5Cxi_i&id=P8ceW),
代表样本
是正样本(1)还是负样本(-1)。而RankSVM是典型的pairwise方法,考虑两个有偏序关系的物品对,训练样本为,则优化目标为:
)%20%5Cgeq%201-%5Cxi%7Buij%7D%2C%20%5Cxi%7Buij%7D%5Cgeq%200%0A%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0A%26%20min%7Bw%2Cb%7D%20%5Cfrac%7B1%7D%7B2%7D%7C%7Cw%7C%7C%5E2%20%2B%20C%5Csum%7Bi%3D1%7D%5En%20%5Cxi%7Buij%7D%20%5C%5C%0As.t.%2C%20%26%20y%7Buij%7D%28w%5ET%28x%7Bu%2Ci%7D-x%7Bu%2Cj%7D%29%29%20%5Cgeq%201-%5Cxi%7Buij%7D%2C%20%5Cxi%7Buij%7D%5Cgeq%200%0A%5Cend%7Bsplit%7D%0A&id=fEtS2)
此时,代表用户
对
的喜爱程度比对
的喜爱程度高时,为1,否则为-1。上述优化等价于优化如下
Hinge Loss:
%5Cin%20%5Cmathcal%7BS%7D%20%5Ccup%20%5Cmathcal%7BD%7D%7D%5B1-%20y%7Buij%7D%5Ccdot%20w%5ET%20x%7Bu%2Ci%7D%2B%20y%7Buij%7D%20%5Ccdot%20w%5ETx%7Bu%2Cj%7D%5D%7B%2B%7D%0A#card=math&code=L%7Bw%7D%3D%5Csum%7B%28u%2Ci%2Cj%29%5Cin%20%5Cmathcal%7BS%7D%20%5Ccup%20%5Cmathcal%7BD%7D%7D%5B1-%20y%7Buij%7D%5Ccdot%20w%5ET%20x%7Bu%2Ci%7D%2B%20y%7Buij%7D%20%5Ccdot%20w%5ETx%7Bu%2Cj%7D%5D%7B%2B%7D%0A&id=YgkkK)
其中,集合中,
,
集合中,
。
#card=math&code=%5Bz%5D_%7B%2B%7D%3Dmax%280%2Cz%29&id=NRCpv)。
上述的改进工作一般是围绕不同pair有序对权重不同展开,即前会加个权重。
Hinge Ranking Loss 是排序学习中非常重要的损失函数之一,大部分做ranking任务的模型都会采用。
RankNet⭐️
RankNet 是 2005 年微软提出的一种经典的Pairwise的排序学习方法,从概率的角度来解决排序问题。RankNet 解决排序的思路其实是把一个 list 排序的问题转化成 list 中两两比较的问题,利用前向神经网络和概率损失函数来学习 Ranking Function,并应用 Ranking Function 对文档进行排序。
这里的 Ranking Function 可以是任意对参数可微的模型,也就是说,该概率损失函数并不依赖于特定的机器学习模型,在论文中,RankNet 是基于神经网络实现的。除此之外,GDBT、LR、MF 等模型也可以应用于该框架。
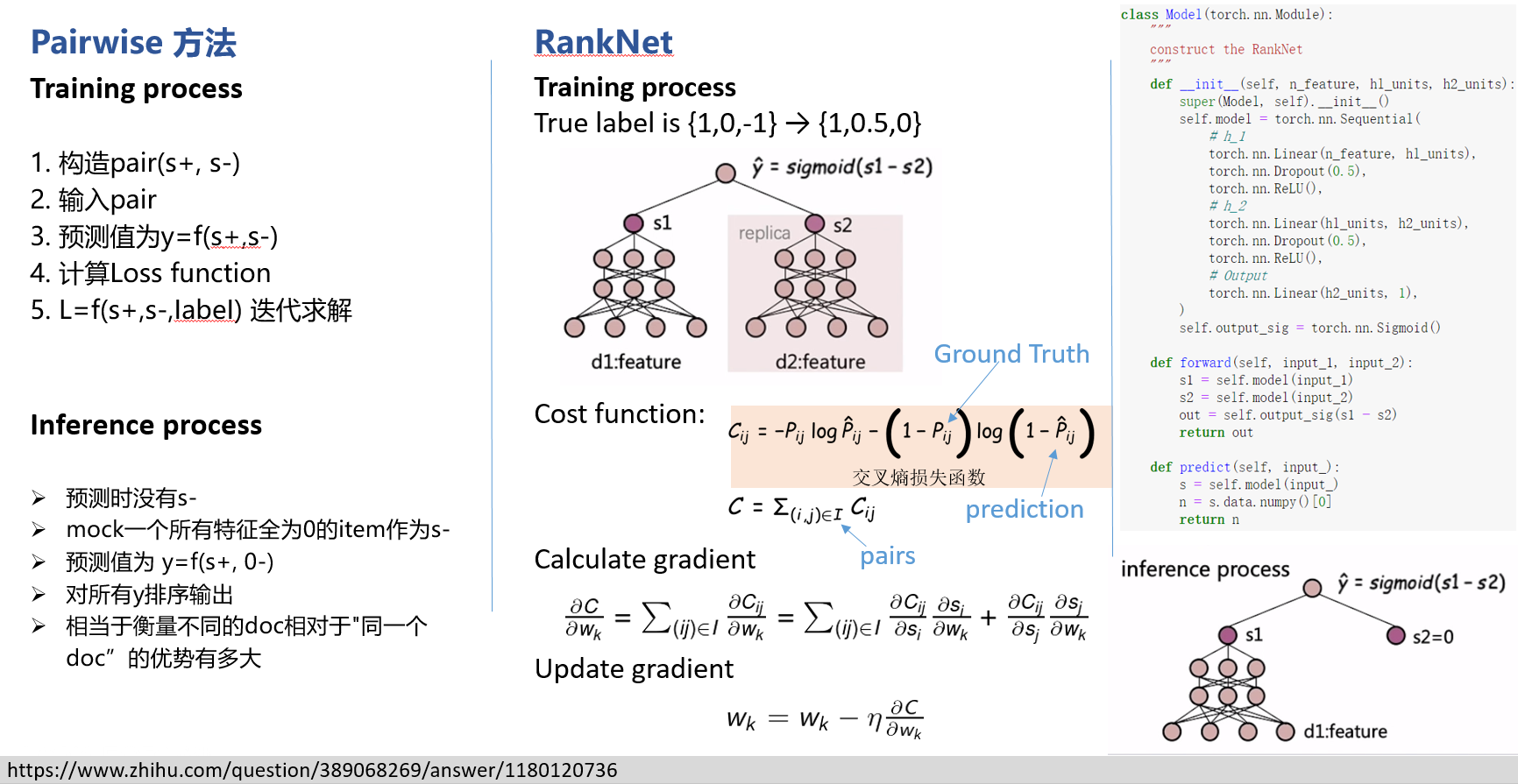
预测相关性概率
RankNet 把排序问题转换成比较一个 #card=math&code=%28U_i%2CU_j%29&id=SqL4f) 文档对的排序概率问题。具体地,给定特定 query 下的两个文档
和
,其特征向量分别为
和
,经过 RankNet 进行前向计算得到对应的分数为
#card=math&code=s_i%3Df%28x_i%29&id=Kc2dx) 和
#card=math&code=s_j%3Df%28x_j%29&id=CoVbr)。用下面的公式来计算同一个Query下
应该比
更相关的概率:
%20%3D%20%5Cfrac%7B1%7D%7B1%20%2B%20%5Cexp%5Cbigl(-%5Csigma%20%5Ccdot%20(si%20-%20s_j)%5Cbigr)%7D%0A#card=math&code=P%7Bij%7D%20%3D%20P%28x_i%20%5Crhd%20x_j%29%20%3D%20%5Cfrac%7B1%7D%7B1%20%2B%20%5Cexp%5Cbigl%28-%5Csigma%20%5Ccdot%20%28s_i%20-%20s_j%29%5Cbigr%29%7D%0A&id=kigvi)
这个概率实际上就是深度学习中经常使用的 sigmoid 函数,由于参数 σ 影响的是 sigmoid 函数的形状,对最终结果影响不大,因此通常默认使用 σ=1 进行简化。
RankNet的加速
RankNet 证明了如果知道一个待排序文档的排列中相邻两个文档之间的排序概率,则通过推导可以算出每两个文档之间的排序概率。因此对于一个待排序文档序列,只需计算相邻文档之间的排序概率,不需要计算所有 pair,减少计算量。
真实相关性概率
对于特定的 query,定义 为文档
和文档
被标记的标签之间的关联,即
我们定义 比
更相关(排序更靠前)的真实概率为:
%0A#card=math&code=%5Cbar%7BP%7D%7Bi%20j%7D%3D%5Cfrac%7B1%7D%7B2%7D%5Cleft%281%2BS%7Bi%20j%7D%5Cright%29%0A&id=zTZhb)
RankNet 的损失函数
对于一个排序,RankNet 从各个 doc 的相对关系来评价排序结果的好坏,排序的效果越好,那么有错误相对关系的 pair 就越少。所谓错误的相对关系即如果根据模型输出 排在
前面,但真实 label 为
的相关性小于
,那么就记一个错误 pair,RankNet 本质上就是以错误的 pair 最少为优化目标,也就是说 RankNet 的目的是优化逆序对数。而在抽象成损失函数时,RankNet 实际上是引入了概率的思想:不是直接判断
排在
前面,而是说
以一定的概率
排在
前面,即是以预测概率与真实概率的差距最小作为优化目标。最后,RankNet 使用交叉熵(Cross Entropy)作为损失函数,来衡量
对
的拟合程度:
%20%5Clog%20%5Cleft(1-P%7Bi%20j%7D%5Cright)%0A#card=math&code=C%3D-%5Cbar%7BP%7D%7Bi%20j%7D%20%5Clog%20P%7Bi%20j%7D-%5Cleft%281-%5Cbar%7BP%7D%7Bi%20j%7D%5Cright%29%20%5Clog%20%5Cleft%281-P_%7Bi%20j%7D%5Cright%29%0A&id=VgoTW)
Ranknet 最终目标是训练出一个打分函数 #card=math&code=s%3Df%28x%3Bw%29&id=yCYgo),使得所有 pair 的排序概率估计的损失最小,即:
%20%5Cin%20I%7D%20C%7Bi%20j%7D%0A#card=math&code=C%3D%5Csum%7B%28i%2C%20j%29%20%5Cin%20I%7D%20C_%7Bi%20j%7D%0A&id=XTPT0)
其中, 表示所有在同一 query 下,且具有不同相关性判断的 doc pair,每个 pair 有且仅有一次。
通常,这个打分函数只要是光滑可导就行,比如 %3Dwx#card=math&code=f%28x%29%3Dwx&id=yTL19) 都可以,RankNet 使用了两层神经网络:
%3Dg%5E%7B3%7D%5Cleft(%5Csum%7Bj%7D%20w%7Bi%20j%7D%5E%7B32%7D%20g%5E%7B2%7D%5Cleft(%5Csum%7Bk%7D%20w%7Bj%20k%7D%5E%7B21%7D%20x%7Bk%7D%2Bb%7Bj%7D%5E%7B2%7D%5Cright)%2Bb%7Bi%7D%5E%7B3%7D%5Cright)%0A#card=math&code=f%28x%29%3Dg%5E%7B3%7D%5Cleft%28%5Csum%7Bj%7D%20w%7Bi%20j%7D%5E%7B32%7D%20g%5E%7B2%7D%5Cleft%28%5Csum%7Bk%7D%20w%7Bj%20k%7D%5E%7B21%7D%20x%7Bk%7D%2Bb%7Bj%7D%5E%7B2%7D%5Cright%29%2Bb%7Bi%7D%5E%7B3%7D%5Cright%29%0A&id=x9UaG)
参数更新
RankNet 采用神经网络模型优化损失函数,也就是后向传播过程,采用梯度下降法求解并更新参数:
其中,η 是学习率,论文中实验时选取的范围是 1e-3 到 1e-5,因为 RankNet 是一种方法框架,因此这里的 wk 可以是 NN、LR、GBDT 等算法的权重。
对RankNet的梯度进行因式分解,有:
%20%5Cin%20P%7D%5Cfrac%7B%5Cpartial%20L%7Bij%7D%7D%7B%5Cpartial%20w_k%7D%20%3D%0A%5Csum%7B(i%2C%20j)%20%5Cin%20P%7D%0A%5Cfrac%7B%5Cpartial%20L%7Bij%7D%7D%7B%5Cpartial%20s_i%7D%5Cfrac%7B%5Cpartial%20s_i%7D%7B%5Cpartial%20w_k%7D%0A%2B%0A%5Cfrac%7B%5Cpartial%20L%7Bij%7D%7D%7B%5Cpartial%20sj%7D%5Cfrac%7B%5Cpartial%20s_j%7D%7B%5Cpartial%20w_k%7D%0A#card=math&code=%5Cfrac%7B%5Cpartial%20L%7D%7B%5Cpartial%20w_k%7D%20%3D%0A%5Csum%7B%28i%2C%20j%29%20%5Cin%20P%7D%5Cfrac%7B%5Cpartial%20L%7Bij%7D%7D%7B%5Cpartial%20w_k%7D%20%3D%0A%5Csum%7B%28i%2C%20j%29%20%5Cin%20P%7D%0A%5Cfrac%7B%5Cpartial%20L%7Bij%7D%7D%7B%5Cpartial%20s_i%7D%5Cfrac%7B%5Cpartial%20s_i%7D%7B%5Cpartial%20w_k%7D%0A%2B%0A%5Cfrac%7B%5Cpartial%20L%7Bij%7D%7D%7B%5Cpartial%20s_j%7D%5Cfrac%7B%5Cpartial%20s_j%7D%7B%5Cpartial%20w_k%7D%0A&id=nDYm7)
不难证明:
%20-%5Cfrac%7B1%7D%7B1%20%2B%20%5Cexp%5Cbigl(%5Csigma%20%5Ccdot%20(si%20-%20s_j)%5Cbigr)%7D%5CBiggr%5D%20%3D%20-%5Cfrac%7B%5Cpartial%20L%7Bij%7D%7D%7B%5Cpartial%20sj%7D%0A#card=math&code=%5Cfrac%7B%5Cpartial%20L%7Bij%7D%7D%7B%5Cpartial%20si%7D%20%3D%20%5Csigma%20%5Ccdot%20%5CBiggl%5B%5Cfrac12%281%20-%20S%7Bij%7D%29%20-%5Cfrac%7B1%7D%7B1%20%2B%20%5Cexp%5Cbigl%28%5Csigma%20%5Ccdot%20%28si%20-%20s_j%29%5Cbigr%29%7D%5CBiggr%5D%20%3D%20-%5Cfrac%7B%5Cpartial%20L%7Bij%7D%7D%7B%5Cpartial%20s_j%7D%0A&id=Mwu3i)
由公式可知,结果排序最终由模型得分 确定,它的梯度很关键,于是我们定义:
.
在构造样本Pair时,我们可以始终令i为更相关的文档,此时始终有 ,于是有简化,
%7D%7D%0A#card=math&code=%5Clambda%7Bi%20j%7D%20%5Cstackrel%7B%5Ctext%20%7B%20def%20%7D%7D%7B%3D%7D-%5Cfrac%7B%5Csigma%7D%7B1%2Be%5E%7B%5Csigma%5Cleft%28s%7Bi%7D-s_%7Bj%7D%5Cright%29%7D%7D%0A&id=AS26J)
这个 就是接下来要介绍的 LambdaRank 和 LambdaMART 中的 Lambda,称为 Lambda 梯度。
RankNet 小结
排序问题的评价指标一般有 NDCG、ERR、MAP、MRR 等,这些指标的特点是不平滑、不连续,无法求梯度,因此无法直接用梯度下降法求解。RankNet 的创新点在于没有直接对这些指标进行优化,而是间接把优化目标转换为可以求梯度的基于概率的交叉熵损失函数进行求解。因此任何用梯度下降法优化目标函数的模型都可以采用该方法,RankNet 采用的是神经网络模型,其他类似 boosting tree 等模型也可以使用该方法求解。
基于Keras的RankNet实现:
# 网络参数def create_base_network(input_dim):seq = Sequential()seq.add(Dense(input_dim, input_shape=(input_dim,), activation='relu'))seq.add(Dropout(0.1))seq.add(Dense(64, activation='relu'))seq.add(Dropout(0.1))seq.add(Dense(32, activation='relu'))seq.add(Dense(1))return seq# Rank Cost层def create_meta_network(input_dim, base_network):input_a = Input(shape=(input_dim,))input_b = Input(shape=(input_dim,))rel_score = base_network(input_a)irr_score = base_network(input_b)# subtract scoresdiff = Subtract()([rel_score, irr_score])# Pass difference through sigmoid function.prob = Activation("sigmoid")(diff)# Build model.model = Model(inputs = [input_a, input_b], outputs = prob)model.compile(optimizer = "adam", loss = "binary_crossentropy")return model
Listwise Ranker
Listwise方法的几个优势:
- 原始数据无需组pair,从而避免了因组pair导致的数据量、数据大小的成倍增长。这也一定程度上加快了训练过程。
- 优化目标为NDCG,通过指定NDCG截断个数,可以忽略大量尾部带噪声的样本的排序,从而集中优化前几位的排序。
- 直接利用原始数据的打分信息进行排序学习,避免了通过分数大小组pair带来的信息损失。
LambdaRank
以错误pair最少为优化目标的RankNet算法,然而许多时候仅以错误pair数来评价排序的好坏是不够的,像NDCG或者ERR等评价指标就只关注top k个结果的排序,当我们采用RankNet算法时,往往无法以这些指标为优化目标进行迭代,所以RankNet的优化目标和IR评价指标之间还是存在gap的。
假设 RankNet 经过两轮迭代实现下图所示的顺序优化:
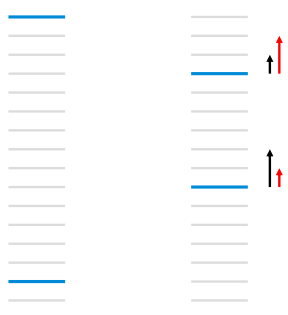
如上图所示,每个线条表示文档,蓝色表示相关文档,灰色表示不相关文档,左图的cost为13,右图通过把第一个相关文档下调3个位置,第二个文档上条5个位置,将cost降为11,但是像NDCG或者ERR等评价指标只关注top k个结果的排序,在优化过程中下调前面相关文档的位置不是我们想要得到的结果。图 1右图左边黑色的箭头表示RankNet下一轮的调序方向和强度,但我们真正需要的是右边红色箭头代表的方向和强度,即更关注靠前位置的相关文档的排序位置的提升。LambdaRank正是基于这个思想演化而来,其中Lambda指的就是红色箭头,代表下一次迭代优化的方向和强度,也就是梯度
RankNet 以优化逆序对数为目标,并没有考虑位置的权重,这种优化方式对 AUC 这类评价指标比较友好,但实际的排序结果与现实的排序需求不一致,现实中的排序需求更加注重头部的相关度,排序评价指标选用 NDCG 这一类的指标才更加符合实际需求。而 RankNet 这种以优化逆序对数为目的的交叉熵损失,并不能直接或者间接优化 NDCG 这样的指标。
我们知道 NDCG 是一个处处非平滑的函数,直接以它为目标函数进行优化是不可行的。那 LambdaRank 又是如何解决这个问题的呢?
我们必须先有这样一个洞察,对于绝大多数的优化过程来说,目标函数很多时候仅仅是为了推导梯度而存在的。而如果我们直接就得到了梯度,那自然就不需要目标函数了。
于是,微软学者经过分析,就直接把 RankNet 最后得到的 Lambda 梯度拿来作为 LambdaRank 的梯度来用了,这也是 LambdaRank 中 Lambda 的含义。这样我们便知道了 LambdaRank 其实是一个经验算法,它不是通过显示定义损失函数再求梯度的方式对排序问题进行求解,而是分析排序问题需要的梯度的物理意义,直接定义梯度,即 Lambda 梯度。有了梯度,就不用关心损失函数是否连续、是否可微了,所以,微软学者直接把 NDCG 这个更完善的评价指标与 Lambda 梯度结合了起来,就形成了 LambdaRank。
我们来分析一下 Lambda 梯度的物理意义。
LambdaRank 中的 Lambd 其实就是 RankNet 中的梯度 ,
可以看成是
和
中间的作用力,代表下一次迭代优化的方向和强度。如果
,则
会给予
向上的大小为
的推动力,而对应地
会给予
向下的大小为
的推动力。对应上面的那张图,Lambda 的物理意义可以理解为图中箭头,即优化趋势,因此有些人也会把 Lambda 梯度称之为箭头函数。
LambdaRank在RankNet的加速算法形式的基础上引入评价指标Z (如NDCG、ERR等),把交换两个文档的位置引起的评价指标的变化 ,作为其中一个因子乘以
就可以得到 LambdaRank 的 Lambda,即:
%7D%7B%5Cpartial%20s%7Bi%7D%7D%3D%5Cfrac%7B-%5Csigma%7D%7B1%2Be%5E%7B%5Csigma%5Cleft(s%7Bi%7D-s%7Bj%7D%5Cright)%7D%7D%5Cleft%7C%5CDelta%7BN%20D%20C%20G%7D%5Cright%7C%0A#card=math&code=%5Clambda%7Bi%20j%7D%20%5Cstackrel%7B%5Ctext%20%7B%20def%20%7D%7D%7B%3D%7D%20%5Cfrac%7B%5Cpartial%20C%5Cleft%28s%7Bi%7D-s%7Bj%7D%5Cright%29%7D%7B%5Cpartial%20s%7Bi%7D%7D%3D%5Cfrac%7B-%5Csigma%7D%7B1%2Be%5E%7B%5Csigma%5Cleft%28s%7Bi%7D-s%7Bj%7D%5Cright%29%7D%7D%5Cleft%7C%5CDelta_%7BN%20D%20C%20G%7D%5Cright%7C%0A&id=G8wOH)
其中 是
和
交换排序位置得到的 NDCG 差值。
NDCG 倾向于将排名高并且相关性高的文档更快地向上推动,而排名低而且相关性较低的文档较慢地向上推动,这样通过引入 IR 评价指标(Information Retrieval 的评价指标包括:MRR,MAP,ERR,NDCG 等)就实现了类似上面图中红色箭头的优化趋势。可以证明,通过此种方式构造出来的梯度经过迭代更新,最终可以达到优化 NDCG 的目的。
当然,我们还可以反推一下 LambdaRank 的损失函数,确切地应该称为效用函数(utility function):
%7D%5Cright)%20%5Ccdot%5Cleft%7C%5CDelta%20Z%7Bi%20j%7D%5Cright%7C%0A#card=math&code=C%7Bi%20j%7D%3D%5Clog%20%5Cleft%281%2Be%5E%7B-%5Csigma%5Cleft%28s%7Bi%7D-s%7Bj%7D%5Cright%29%7D%5Cright%29%20%5Ccdot%5Cleft%7C%5CDelta%20Z_%7Bi%20j%7D%5Cright%7C%0A&id=TEfRZ)
这里的 泛指可用的评价指标,但最常用的还是 NDCG。
总结一下,LambdaRank提供了一种思路:绕过目标函数本身,直接构造一个特殊的梯度,按照梯度的方向修正模型参数,最终能达到拟合NDCG的方法[6]。LambdaRank 的主要突破点:
- 分析了梯度的物理意义;
- 绕开损失函数,直接定义梯度。
LambdaMART⭐️
- Mart(Multiple Additive Regression Tree,Mart就是GBDT),定义了一个框架,缺少一个梯度。
- LambdaRank重新定义了梯度,赋予了梯度新的物理意义。
LambdaRank 重新定义了梯度,赋予了梯度新的物理意义,因此,所有可以使用梯度下降法求解的模型都可以使用这个梯度,基于决策树的 MART 就是其中一种,将梯度 Lambda 和 MART 结合就是大名鼎鼎的 LambdaMART。LambdaMART是LambdaRank的 gbdt 版本,而LambdaRank又是基于pairwise的RankNet。因此LambdaMART本质上也是属于pairwise排序算法,只不过引入Lambda梯度后,还显示的考察了列表级的排序指标,如NDCG等,因此,也可以算作是listwise的排序算法。LambdaMART由微软于2010年的论文Adapting Boosting for Information Retrieval Measures提出,截止到2018.12.12,引用量达到308。本小节主要介绍LambdaMART,参考文章 From RankNet to LambdaRank toLambdaMART: An Overview。
LambdaMART是基于 LambdaRank 算法和 MART (Multiple Additive Regression Tree) 算法,将排序问题转化为回归决策树问题。GBDT 的核心思想是在不断的迭代中,新一轮迭代产生的回归决策树模型拟合损失函数的梯度,最终将所有的回归决策树叠加得到最终的模型。LambdaMART 使用一个特殊的 Lambda 值来代替上述梯度,也就是将 LambdaRank 算法与 MART 算法结合起来,是一种能够支持非平滑损失函数的学习排序算法。
LambdaMART 在 GBDT 的过程中做了一个很小的修改。原始 GBDT 的原理是直接在函数空间对函数进行求解模型,结果由许多棵树组成,每棵树的拟合目标是损失函数的梯度,而在 LambdaMART 中这个梯度就换成了 Lambda 梯度,这样就使得 GBDT 并不是直接优化二分分类问题,而是一个改装了的二分分类问题,也就是在优化的时候优先考虑能够进一步改进 NDCG 的方向。
由此,LambdaMART的具体算法过程如下:

可以看出LambdaMART的框架其实就是MART,主要的创新在于中间计算的梯度使用的是Lambda,是pairwise的。MART需要设置的参数包括:树的数量M、叶子节点数L和学习率v,这3个参数可以通过验证集调节获取最优参数。
MART输出值的计算:
- 首先设置每棵树的最大叶子数,基分类器通过最小平方损失进行分裂,达到最大叶子数量时停止分裂
- 使用牛顿法得到叶子的输出,计算效用函数对模型得分的二阶导
%0A#card=math&code=%5Cfrac%7B%5Cpartial%5E%7B2%7D%20C%7D%7B%5Cpartial%5E%7B2%7D%20s%7Bi%7D%7D%3D%5Csum%7B%5C%7Bi%2C%20j%5C%7D%3DI%7D%20%5Csigma%5E%7B2%7D%5Cleft%7C%5CDelta%20Z%7Bi%20j%7D%5Cright%7C%20%5Crho%7Bi%20j%7D%5Cleft%281-%5Crho_%7Bi%20j%7D%5Cright%29%0A&id=gKEO2)
- 得到第m颗树的第k个叶子的输出值:
%7D%0A#card=math&code=%5Cgamma%7Bk%20m%7D%3D%5Cfrac%7B%5Csum%7Bx%7Bi%7D%20%5Cin%20R%7Bk%20m%7D%7D%20%5Cfrac%7B%5Cpartial%20C%7D%7B%5Cpartial%20s%7Bi%7D%7D%7D%7B%5Csum%7Bx%7Bi%7D%20%5Cin%20R%7Bk%20m%7D%7D%20%5Cfrac%7B%5Cpartial%5E%7B2%7D%20C%7D%7B%5Cpartial%5E%7B2%7D%20s%7Bi%7D%7D%7D%3D%5Cfrac%7B-%5Csum%7Bx%7Bi%7D%20%5Cin%20R%7Bk%20m%7D%7D%20%5Csum%7B%5C%7Bi%2C%20j%5C%7D%20%5Crightleftharpoons%20I%7D%5Cleft%7C%5CDelta%20Z%7Bi%20j%7D%5Cright%7C%20%5Crho%7Bi%20j%7D%7D%7B%5Csum%7Bx%7Bi%7D%20%5Cin%20R%7Bk%20m%7D%7D%20%5Csum%7B%5C%7Bi%2C%20j%5C%7D%20%5Crightleftharpoons%20I%7D%5Cleft%7C%5CDelta%20Z%7Bi%20j%7D%5Cright%7C%20%5Csigma%20%5Crho%7Bi%20j%7D%5Cleft%281-%5Crho%7Bi%20j%7D%5Cright%29%7D%0A&id=o9KKe)
为第i个样本,
意味着落入该叶子的样本,这些样本共同决定了该叶子的输出值。
LambdaMART 具有很多优势:
- 适用于排序场景:不是传统的通过分类或者回归的方法求解排序问题,而是直接求解;
- 损失函数可导:通过损失函数的转换,将类似于 NDCG 这种无法求导的 IR 评价指标转换成可以求导的函数,并且富有了梯度的实际物理意义,数学解释非常漂亮;
- 增量学习:由于每次训练可以在已有的模型上继续训练,因此适合于增量学习;
- 组合特征:因为采用树模型,因此可以学到不同特征组合情况;
- 特征选择:因为是基于 MART 模型,因此也具有 MART 的优势,每次节点分裂选取 Gain 最⼤的特征,可以学到每个特征的重要性,因此可以做特征选择;
- 适用于正负样本比例失衡的数据:因为模型的训练对象具有不同 label 的文档 pair,而不是预测每个文档的 label,因此对正负样本比例失衡不敏感。
PS: 需要注意的是,LmabdaRank 和 LambdaMART 虽然看起来很像配对法(Pairwise),但其实都属列表法(Listwise),确切来说是 Listwise 和 Pairwise 之间的一种混合方法。列表法从理论上和研究情况来看,都是比较理想的排序学习方法。因为列表法尝试统一排序学习的测试指标和学习目标。尽管在学术研究中,纯列表法表现优异,但是在实际中,类似于 LambdaRank 和 LambdaMART 这类思路,也就是基于配对法和列表法之间的混合方法更受欢迎。因为从总体上看,纯列表法的运算复杂度都比较高,而在工业级的实际应用中,真正的优势并不是特别大,因此纯列表法的主要贡献目前还多是学术价值。
PS: LambdaMART是LambdaRank的提升树版本,而LambdaRank又是基于pairwise的RankNet。因此LambdaMART本质上也是属于pairwise排序算法,只不过引入Lambda梯度后,还显示的考察了列表级的排序指标,如NDCG等,因此,也可以算作是listwise的排序算法。
Summary: From RankNet to LambdaRank to LambdaMART
| RankNet | LambdaRank | LambdaMART | |
|---|---|---|---|
| Object | Cross entropy over the pairs | Unknown | Unknown |
| Gradient (λ function) | Gradient of cross entropy | Gradient of cross entropy timespairwisechange in target metric | Gradient of cross entropy timespairwisechange in target metric |
| Optimization method | neural network | stochastic gradient descent | Multiple Additive Regression Trees (MART) |
Ranking Metric Optimization
前面我们提到,不管是pointwise还是pairwise都不能直接优化排序度量指标。在listwise中,我们通过定义Lambda梯度来优化排序度量指标,如LambdaRank和LambdaMART,然后Lambda梯度是一种经验性方法,缺乏理论指导。最近,有研究者提出了优化排序度量指标的概率模型框架,叫做LambdaLoss(CIKM18: The LambdaLoss Framework for Ranking Metric Optimization),提供了一种EM算法来优化Metric驱动的损失函数。文中提到LambdaRank中的Lambda梯度在LambdaLoss框架下,能够通过定义一种良好、特殊设定的损失函数求解,提供了一定的理论指导。
传统的pointwise或pairwise损失函数是平滑的凸函数,很容易进行优化。有些工作已经证明优化这些损失的结果是真正排序指标的界,即实际回归或分类误差是排序指标误差(取反)的上界(bound)。但是这个上界粒度比较粗,因为优化不是metric驱动的。
然而,直接优化排序指标的挑战在于,排序指标依赖于列表的排序结果,而列表的排序结果又依赖于每个物品的得分,导致排序指标曲线要么不是平坦的,要么不是连续的,即非平滑,也非凸。因此,梯度优化方法不实用,尽管有些非梯度优化方法可以用,但是时间复杂度高,难以规模化。为了规模化,目前有3种途径,1是近似法,缺点是非凸,容易陷入局部最优;2是将排序问题转成结构化预测问题,在该方法中排序列表当做最小单元来整体对待,损失定义为实际排序列表和最理想排序列表之间的距离,缺点是排序列表排列组合数量太大,复杂度高;3是使用排序指标在迭代过程中不断调整样本的权重分布(回顾下WRAP就是这种,LambdaRank也属于这种,|ΔNDCG||ΔNDCG|就可以看做是权重。),这个方法优点是既考虑了排序指标,同时也是凸优化问题。
本文的动机之一就是探索LambdaRank中提出的Lambda梯度真正优化的损失函数是什么。文章通过提出LambdaLoss概率框架,来解释LambdaRank可以通过EM算法优化LambdaLoss得到。进一步,可以在LambdaLoss框架下,定义基于排序和得分条件下,metric-driven的损失函数。
无偏 Learning-to-Rank
先前的研究表明,受到排版的影响,给定排序的项目列表,无论其相关性如何,用户更有可能与前几个结果进行交互,这实际上是一种位置偏差(Position Bias),即,被交互和用户真正喜欢存在差距,因为靠前,人们更倾向于交互,而很多靠后未点击的物品,用户可能更感兴趣,倘若将这些靠后的物品挪到前面去,那用户交互的概率可能会更高。 这一观察激发了研究人员对无偏见的排序学习(Unbiased Learning-to-Rank)的兴趣。常见的解决途径包括,对训练实例重新赋权来缓解偏差;构造无偏差损失函数进行无偏排序学习;评估时使用无偏度量指标等。
总结
搜索引擎时敲定特征分的权重是非常疼的一件事儿,而LTR正好帮你定分,LTR的三种实现方法其实各有优劣:
- 难点主要在训练样本的构建(人工或者挖日志),另外就是训练复杂
- 虽说Listwise效果最好,pointwise使用还是比较多,参考这篇文章综述LTR体验下
- 在工业界用的比较多的应该还是Pairwise,因为他构建训练样本相对方便,并且复杂度也还可以,所以Rank SVM就很火
未来展望
对于CTR预估和排序学习的领域,目前深度学习尚未在自动特征挖掘上对人工特征工程形成碾压之势,因此人工特征工程依然很重要(参考)
- 基于深度学习的CTR预估模型改造
- 基于Lambda梯度,通过深度网络进行反向传播,训练一个优化NDCG的深度网络LambdaDNN;
- DSSM model. This method significantly outperforms the traditional lexical ranking model, e.g., TF-IDF and BM25.
- Bert. It have achieved more impressive results on the passage re-ranking task
- 模型组合(GBDT+LR,Deep&Wide等)
参考资料
1 [延伸]Tie-Yan Liu. Learning to Rank for Information Retrieval. Springer↩
2 [延伸]Hang Li. Learning to rank for information retrieval and natural language processing↩
3 [延伸]Li Hang. A Short Introduction to Learning to Rank↩
7 吴佳金等. 改进 Pairwise 损失函数的排序学习方法. 知网↩
8 ★ 美团技术团队. 深入浅出排序学习:写给程序员的算法系统开发实践↩
★ BERT在美团搜索核心排序的探索和实践 - 业界良心总结
9 路明东的博客. 推荐系统技术演进趋势:从召回到排序再到重排
10 Christopher J.C. Burges. From RankNet to LambdaRank to LambdaMART: An Overview. Microsoft↩
11 笨兔勿应. Learning to Rank 算法介绍. cnblogs↩
12 RL-Learning. 机器学习排序算法:RankNet to LambdaRank to LambdaMART. cnblogs↩
13 huagong_adu. Learning To Rank 之 LambdaMART 的前世今生. CSDN↩
小菜鸡. Learning to rank算法(2019-11-18)
★ 小菜鸡. LambdaMART从放弃到入门(2020-03-27)
★ 排序学习调研
对比各种wise的优缺点:https://blog.csdn.net/lipengcn/article/details/80373744
★ Introduction to Learning to Rank - 可用于快速复习掌握要点和核心代码


