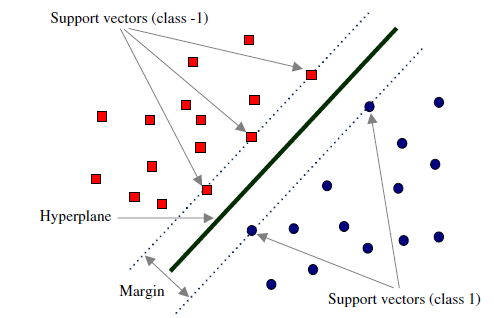
基于支持向量机(support vector machine, SVM)的分类方法主要用于解决二元模式分类问题。支持向量机分类法就是要在训练集中找到具有最大类间界限(margin)的决策平面,使超平面与两类训练集之间的距离最大化,其学习策略(分割原则)便是间隔最大化,最终可转换为一个凸二次规划问题的求解。支持向量机在分类方面具有良好的性能,它在模式识别、图像识别以及自然语言处理等相关技术研究中得到了广泛的应用。
假设上图中的超平面可以用分类函数 f(x) 表示如下:
%3Dw%5ETx%2Bb%0A#card=math&code=f%28x%29%3Dw%5ETx%2Bb%0A&id=ZlGwR)
其中 w 为法向量,决定了超平面的方向,b为位移量,决定了超平面与原点的距离。
假设超平面能将训练样本正确的分类,即对训练样本(xi, yi),满足以下公式:
该公式称为最大间隔假设, 表示样本为正样本,
表示样本为负样本。当 f(x)=0 的时候,x便是位于超平面上的点,而 f(x) > m 的点对应 y=1 的数据点,f(x) < -m 的点对应 y = -1的点。
如何找到最大间隔超平面呢?我们可以先选择分离两类数据的两个平行超平面,使得它们之间的距离尽可能大。在这两个超平面范围内的区域称为“间隔(margin)”,最大间隔超平面是位于它们正中间的超平面。根据几何间隔,margin 的计算公式为:
我们的目标是使 最大, 等价于使
最大:
上式的 是为了后续求导后刚好能消去,没有其他特殊意义。
间隔最大化问题的数学表达就是:
%3D%5Cmin%20%7BW%2C%20b%7D%20%5Cfrac%7B1%7D%7B2%7D%5C%7CW%5C%7C%5E%7B2%7D%20%5C%5C%0A%5Ctext%20%7B%20s.t.%20%7D%20%5Cquad%20y%7Bi%7D%5Cleft(X%7Bi%7D%5E%7BT%7D%20W%2Bb%5Cright)%20%5Cgeq%201%2C%20i%3D1%2C2%2C%20%5Cldots%20n%0A%5Cend%7Barray%7D%0A#card=math&code=%5Cbegin%7Barray%7D%7Bl%7D%0A%5Cmin%20%7BW%2C%20b%7D%20J%28W%29%3D%5Cmin%20%7BW%2C%20b%7D%20%5Cfrac%7B1%7D%7B2%7D%5C%7CW%5C%7C%5E%7B2%7D%20%5C%5C%0A%5Ctext%20%7B%20s.t.%20%7D%20%5Cquad%20y%7Bi%7D%5Cleft%28X_%7Bi%7D%5E%7BT%7D%20W%2Bb%5Cright%29%20%5Cgeq%201%2C%20i%3D1%2C2%2C%20%5Cldots%20n%0A%5Cend%7Barray%7D%0A&id=wzZjl)
通过求解上式即可得到最优超平面 W 和 b.

