2022-03-25-[ML]-激活函数总结

本文参考自《Google软件工程师解读：深度学习的activation function哪家强？》

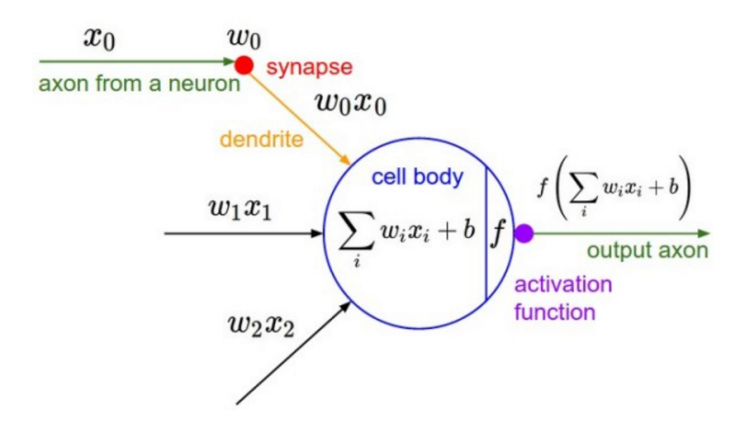
深度学习的基本原理是基于人工神经网络，输入信号经过非线性的active function，传入到下一层神经元；再经过下一层神经元的activate，继续往下传递，如此循环往复，直到输出层。正是因为这些active functions的堆砌，深度学习才被赋予了解决非线性问题的能力，有足够的capacity来抓取复杂的pattern，在各个领域取得state-of-the-art的结果。显而易见，activation function在深度学习中举足轻重，也是很活跃的研究领域之一。

下面我们简单聊一下各类函数的特点以及为什么现在优先推荐ReLU函数。

激活函数概述

1、为什么需要激活函数？
答：激活函数，是指保留特征，去除一些数据中是的冗余

2、active functions应该具备的性质？
答：

• 非线性
• 可微性：当优化方法是基于梯度的时候，这个性质是必须的。
• 单调性：当激活函数是单调的时候，单层网络能够保证是凸函数。
• 𝑓(𝑥)≈𝑥：当激活函数满足这个性质的时候，如果参数的初始化是random的很小的值，那么神经网络的训练将会很高效；如果不满足这个性质，那么就需要很用心的去设置初始值。
• 输出值的范围：当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是无限的时候，模型的训练会更加高效，不过在这种情况小，一般需要更小的learning rate.

3、怎么选用激活函数？
答：建议使用ReLU函数，但是要注意初始化和learning rate的设置；可以尝试使用Leaky ReLU或ELU函数；不建议使用tanh，尤其是sigmoid函数。

sigmoid 介绍

sigmoid函数是深度学习中最基本，也是最为常见的一种激活函数。sigmoid函数公式如下：

sigmoid函数的导函数形式为：

PS： sigmoid导数具体的推导过程如下：

函数曲线和导函数曲线分别如下图所示：

sigmoid函数的优点在于函数平滑且易于求导，但是其缺点也比较突出，例如：

• 容易出现梯度弥散（具体可参考博文《[Deep Learning] 深度学习中消失的梯度》）
• 输出不具有zero-centered性质
• 幂运算相对比较耗时

1.梯度消失Gradient Vanishing

优化神经网络的方法是Back Propagation，即导数的后向传递：先计算输出层对应的loss，然后将loss以导数的形式不断向上一层网络传递，修正相应的参数，达到降低loss的目的。 Sigmoid函数在深度网络中常常会导致导数逐渐变为0，使得参数无法被更新，神经网络无法被优化。

原因有两点：

1. 在上图中容易看出，当中较大或较小时，导数接近0，而后向传递的数学依据是微积分求导的链式法则，当前层的导数需要之前各层导数的乘积，几个小数的相乘，结果会很接近0
2. Sigmoid导数的最大值是0.25，这意味着导数在每一层至少会被压缩为原来的1/4，通过两层后被变为1/16，…，通过10层后为1/1048576。请注意这里是“至少”，导数达到最大值这种情况还是很少见的。

2.输出不是zero-centered

Sigmoid函数的输出值恒大于0，这会导致模型训练的收敛速度变慢。

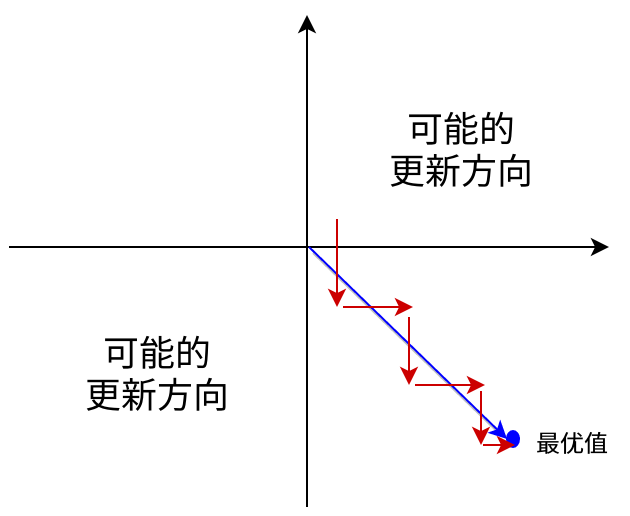
举例来讲，如果所有均为正数或负数，那么其对的导数总是正数或负数，这会导致如下图红色箭头所示的阶梯式更新，这显然并非一个好的优化路径。深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。

3.幂运算相对耗时

相对于前两项，这其实并不是一个大问题，我们目前是具备相应计算能力的，但面对深度学习中庞大的计算量，最好是能省则省 :-)。之后我们会看到，在ReLU函数中，需要做的仅仅是一个thresholding，相对于幂运算来讲会快很多。

Tanh 介绍

tanh读作hyperbolic tangent，相对于sigmoid函数的缺点，它具有zero-centered形式的输出，因此被认为tanh一般总是好于sigmoid，因为函数值介于[-1,1]之间，激活函数的平均值接近于0，这样可以使得下一层的神经元学习的更好。其公式表示如下：

对应的导数形式为：
函数曲线和导函数曲线分别如下图所示：

实际上tanh是sigmoid平移后的结果。因为tanh总是优于sigmoid，所以sigmoid目前基本不用，但有一个例外的场景，那就是sigmoid更适合于做二分类系统的输出层。因为sigmoid的输出值介于[0,1]之间，可以很容易的去表征概率。

ReLU 介绍

近年来，ReLU 变的越来越受欢迎。它的数学表达式如下：

ReLU函数的导函数形式为：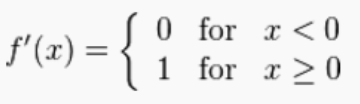
函数曲线和导函数曲线分别如下图所示：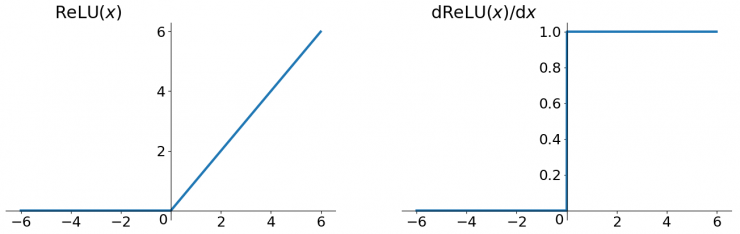

通过上图可以发现，ReLU在0点是不可导的，因此ReLU在应用的时候有个小trick，在实践的时候可以将0点的导数强制赋值为0或者1。

ReLU虽然简单，但却是深度学习激活函数方面几乎最为重要的成果，它有以下几大优点：

• 解决了梯度弥散的问题（输出均大于0）
• 计算速度非常快，只需要判断输入是否大于0（阈值计算）
• 收敛速度远快于sigmoid和tanh

但其实ReLU也不是万能的，它的缺点可以简单提两点：

• 输出不是zero-centered
• 具有dying ReLU problem

dying ReLU problem：由于ReLU特殊的函数形式，在训练过程中某些神经元可能永远不会被激活，导致相应的参数永远不能被更新，而且这个问题会随着训练的进行持续恶化。
导致dying ReLU problem的原因主要有两个：

• 初始化，这种概率比较小
• Learning rate太大，导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

尽管存在这两个问题，ReLU目前仍是最常用的activation function，在搭建人工神经网络的时候推荐优先尝试！

Leaky ReLU

Leaky ReLU就是针对dying ReLU problem而进行改进的，相对于ReLU而言，函数前半段不再为0，而是一段线性函数。用公式表达如下：

其中，参数𝛼一般为远小于1的实数，比如0.01。
Leaky ReLU函数的导函数形式为：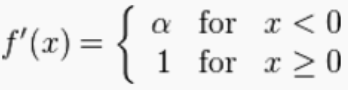
下图显示了Leaky ReLU的两种函数形式，一种𝛼为定值，另外一种𝛼为某范围内的随机值（也被称为Randomized Leaky ReLU）：

除了具备ReLU的所有优点以外，Leaky ReLU不存在dying ReLU problem。从理论上讲，Leaky ReLU应该完全优于ReLU的性能，但是实际应用中并没有表现可以证明Leaky ReLU绝对优于ReLU。

ELU

同Leaky ReLU一样，ELU（Exponential Linear Unit）也是针对dying ReLU problem提出的。具体公式如下：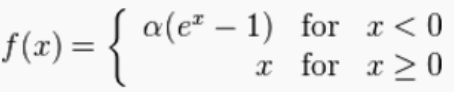

ELU函数的导函数形式为：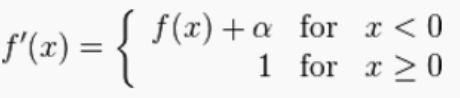
具体函数曲线如下：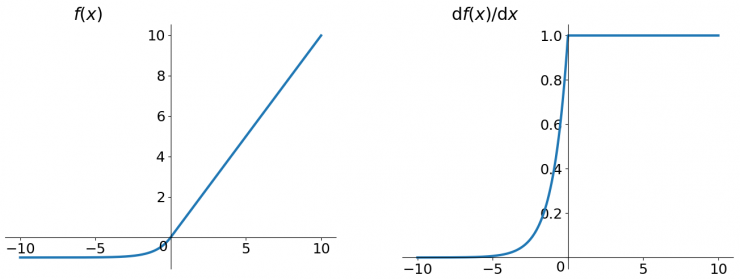

ELU也可以有效地解决dying ReLU problem，而且是近似zero-centered，但随之而来的缺点就是ELU不再是简单的阈值计算，计算相对ReLU稍加复杂。

Active functions汇总

下表汇总了常用的一些active functions：