Transformer
Transformer抛弃了传统的CNN和RNN，整个网络结构完全是由Attention机制组成。更准确地讲，Transformer由且仅由self-Attenion和Feed Forward Neural Network组成。一个基于Transformer的可训练的神经网络可以通过堆叠Transformer的形式进行搭建，作者的实验是通过搭建编码器和解码器各6层，总共12层的Encoder-Decoder，并在机器翻译中取得了BLEU值得新高。
Transformer 有哪些优势呢？
- Transformer摆脱了nlp任务对于rnn，lstm的依赖，在长距离上的建模能力更强；
- 使用了
self-attention可以并行化地对上下文进行建模，提高了训练和推理的速度； - Transformer也是后续更强大的nlp预训练模型的基础（bert系列使用了transformer的encoder，gpt系列transformer的decoder）
Transformer-Encoder
Transformer 包括编码器和解码器两部分。本节主要介绍Transformer的编码器部分，其结构如图2.5（a）所示。它主要包括位置编码（Position Embedding）、多头注意力（Multi-Head Attention）以及前馈神经网络：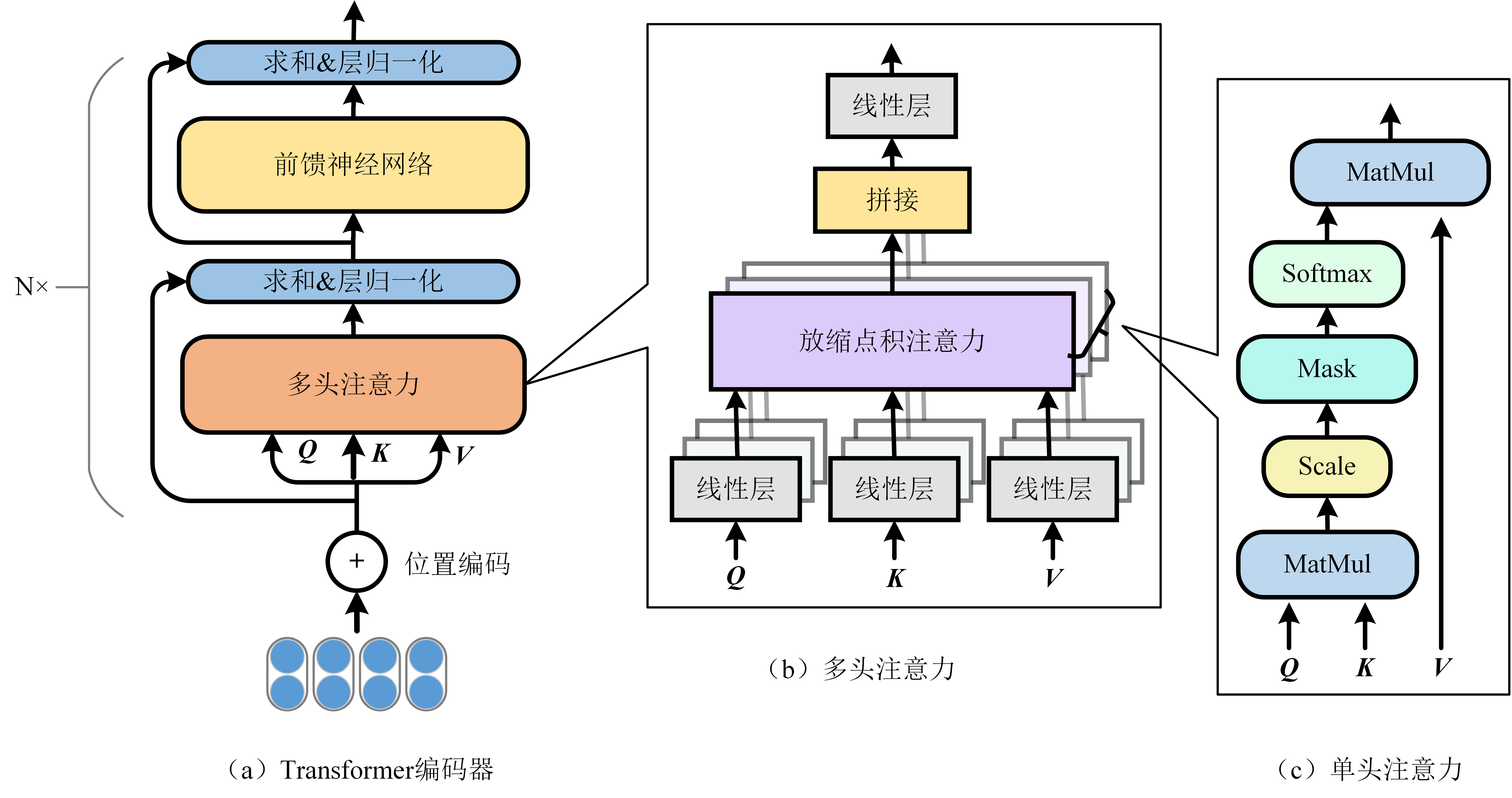
Position Embedding
让研究人员绞尽脑汁的Transformer位置编码-科学空间 Transformer Positional Embeddings and Encodings
我们知道，文字的先后顺序，很重要。比如吃饭没、没吃饭、没饭吃、饭吃没、饭没吃，同样三个字，顺序颠倒，所表达的含义就不同了。
不同于RNN、CNN等模型，对于Transformer模型来说，位置编码的加入是必不可少的，因为纯粹的Attention模块是无法捕捉输入顺序的，即无法区分不同位置的Token。为此我们大体有两个选择：1、想办法将位置信息融入到输入中，这构成了绝对位置编码的一般做法；2、想办法微调一下Attention结构，使得它有能力分辨不同位置的Token，这构成了相对位置编码的一般做法。
- 绝对位置编码是相对简单的一种方案，①可以直接将位置编码当作可训练参数，比如最大长度为512，编码维度为768，那么就初始化一个 512×768 的矩阵作为位置向量，让它随着训练过程更新。现在的BERT、GPT等模型所用的就是这种位置编码；②三角函数式位置编码，一般也称为Sinusoidal位置编码，是Google的论文《Attention is All You Need》所提出来的一个显式解，下文会详细介绍；③先接一层RNN学习位置信息，然后再接Transformer，那么理论上就不需要加位置编码了。
- 输入
与绝对位置编码
的组合方式一般是
- 输入
- 相对位置并没有完整建模每个输入的位置信息，而是在算Attention的时候考虑当前位置与被Attention的位置的相对距离，由于自然语言一般更依赖于相对位置，所以相对位置编码通常也有着优秀的表现。对于相对位置编码来说，它的灵活性更大，更加体现出了研究人员的“天马行空”。
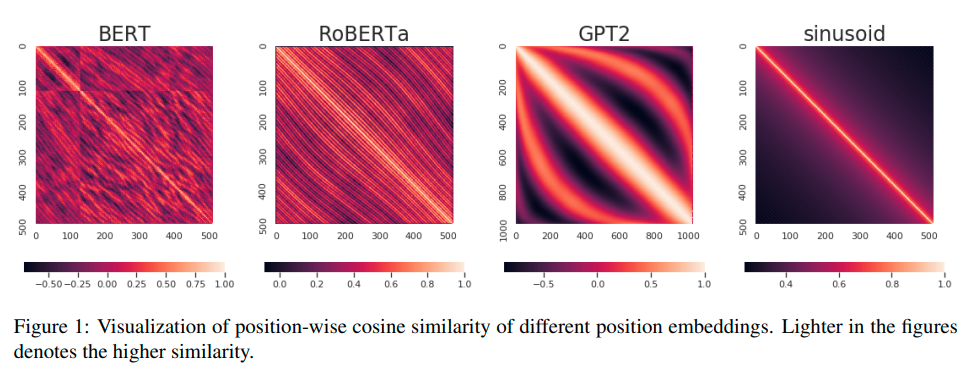
为了能够对位置信息进行编码，Transformer为序列中的每个单词引入了位置编码特征。通过融合词向量和位置向量，来为每一个词引入了一定的位置信息。Tranformer 采用的是 sin-cos 三角函数式位置编码，计算公式如下：
其中， pos 表示位置编号，目标是将其被映射为一个
维的位置向量，该向量的第
个元素值通过公式
进行计算。由于
以及，这表明位置α+β的向量可以表示成位置α和位置β的向量组合，这提供了表达相对位置信息的可能性。但很奇怪的是，现在我们很少能看到直接使用这种形式的绝对位置编码的工作，原因不详。
可以用代码，简单看下效果：
# 导入依赖库import numpy as npimport matplotlib.pyplot as pltimport seaborn as snsimport mathdef get_positional_encoding(max_seq_len, embed_dim):# 初始化一个positional encoding# embed_dim: 字嵌入的维度# max_seq_len: 最大的序列长度positional_encoding = np.array([[pos / np.power(10000, 2 * i / embed_dim) for i in range(embed_dim)]if pos != 0 else np.zeros(embed_dim) for pos in range(max_seq_len)])positional_encoding[1:, 0::2] = np.sin(positional_encoding[1:, 0::2]) # dim 2i 偶数positional_encoding[1:, 1::2] = np.cos(positional_encoding[1:, 1::2]) # dim 2i+1 奇数# 归一化, 用位置嵌入的每一行除以它的模长# denominator = np.sqrt(np.sum(position_enc**2, axis=1, keepdims=True))# position_enc = position_enc / (denominator + 1e-8)return positional_encodingpositional_encoding = get_positional_encoding(max_seq_len=100, embed_dim=16)plt.figure(figsize=(10,10))sns.heatmap(positional_encoding)plt.title("Sinusoidal Function")plt.xlabel("hidden dimension")plt.ylabel("sequence length")
Attention层
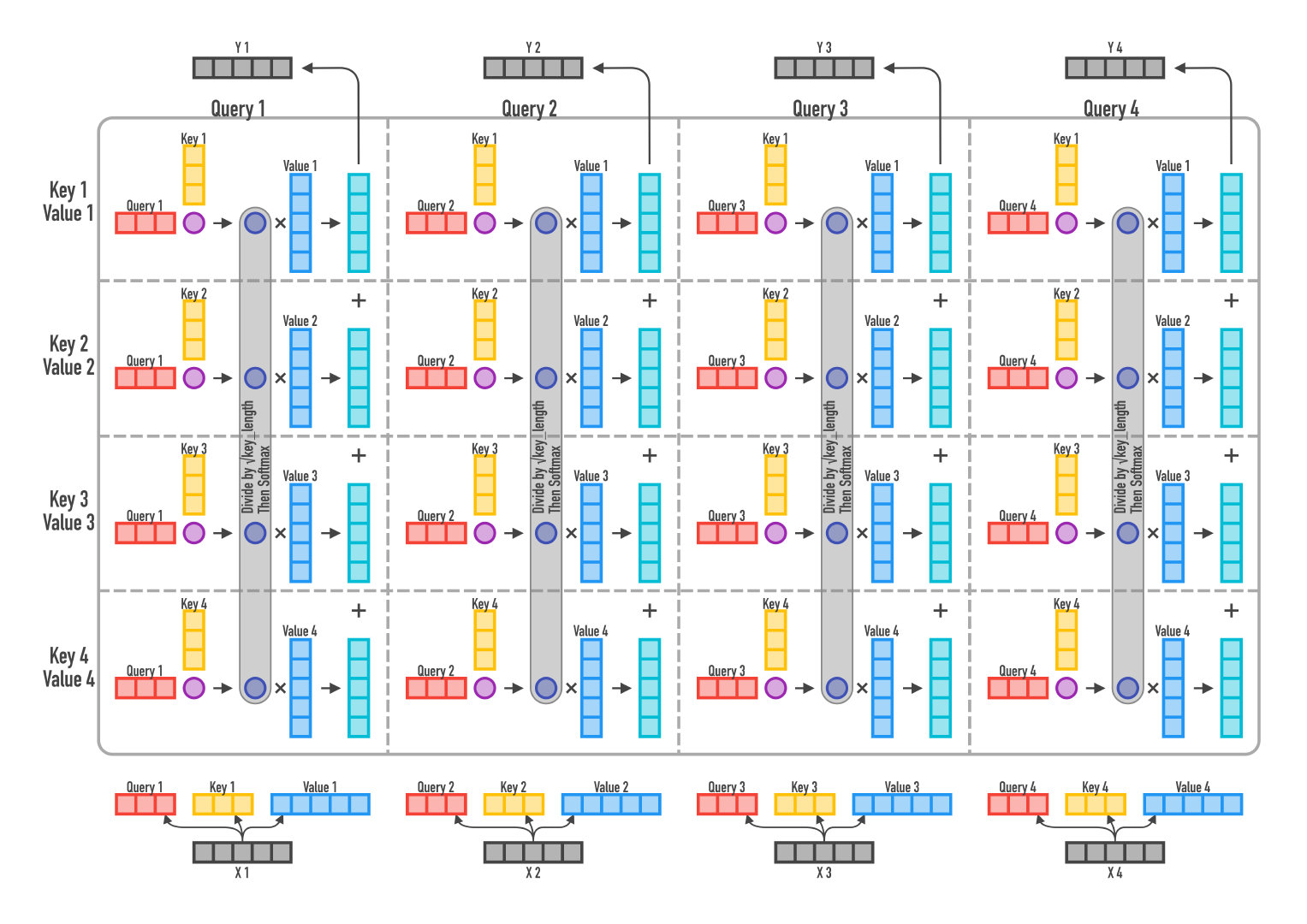
Attention层的好处是能够**一步到位捕捉到全局的联系**，因为它直接把序列两两比较（代价是计算量变为 #card=math&code=O%28n%5E2%29&id=uyZ96)，当然由于是纯矩阵运算，这个计算量相当也不是很严重）；相比之下，RNN需要一步步递推才能捕捉到，而CNN则需要通过层叠来扩大感受野，这是Attention层的明显优势。
Google给出的Attention的定义:%3Dsoftmax(%5Cfrac%7BQK%5ET%7D%7B%5Csqrt%7Bd_k%7D%7D)V%0A#card=math&code=%7BAttention%7D%28Q%2C%20K%2C%20V%29%3Dsoftmax%28%5Cfrac%7BQK%5ET%7D%7B%5Csqrt%7Bd_k%7D%7D%29V%0A&id=fTIbH)
其中，
。单头注意力通过「放缩点积注意力」（Scaled dot-product attention）来将查询
与
进行点积并缩放，再馈送到Softmax函数以获得与
对应的相似度权重。根据这些权重对序列自身
进行加权求和，建模序列内部联系，从而得到
个
维的输出向量。其中因子
起到调节作用，使得内积不至于太大。
逐个向量来看:%3D%5Csum%7Bs%3D1%7D%5E%7Bm%7D%20%5Cfrac%7B1%7D%7BZ%7D%20%5Cexp%20%5Cleft(%5Cfrac%7B%5Cleft%5Clangle%5Cboldsymbol%7Bq%7D%7Bt%7D%2C%20%5Cboldsymbol%7Bk%7D%7Bs%7D%5Cright%5Crangle%7D%7B%5Csqrt%7Bd%7Bk%7D%7D%7D%5Cright)%20%5Cboldsymbol%7Bv%7D%7Bs%7D%0A#card=math&code=Attention%20%5Cleft%28%5Cboldsymbol%7Bq%7D%7Bt%7D%2C%20%5Cboldsymbol%7BK%7D%2C%20%5Cboldsymbol%7BV%7D%5Cright%29%3D%5Csum%7Bs%3D1%7D%5E%7Bm%7D%20%5Cfrac%7B1%7D%7BZ%7D%20%5Cexp%20%5Cleft%28%5Cfrac%7B%5Cleft%5Clangle%5Cboldsymbol%7Bq%7D%7Bt%7D%2C%20%5Cboldsymbol%7Bk%7D%7Bs%7D%5Cright%5Crangle%7D%7B%5Csqrt%7Bd%7Bk%7D%7D%7D%5Cright%29%20%5Cboldsymbol%7Bv%7D_%7Bs%7D%0A&id=R60Yi)
其中， 分别是
的简写，
是一一对应的，它们就像是key-value的关系，那么上式的意思就是通过 这个query，通过与各个 内积的并softmax的方式，来得到 与各个 的相似度，然后加权求和，得到一个 维的向量
。其中因子
起到调节作用，使得内积不至于太大（太大的话softmax后就非0即1了，不够“soft”了）。
结果：将的序列
编码成了一个新的
的序列.
所谓Self Attention，其实就是#card=math&code=Attention%28X%2CX%2CX%29&id=qZuNO)，
就是前面说的输入序列。也就是说，在序列内部做Attention，寻找序列内部的联系。
Multi-Head Attention
所谓“多头”指的是同样的操作（参数不共享）重复多遍，然后把结果拼接起来。多头注意力的结构如图2.5（b）所示，把通过参数矩阵映射一下，然后做单头注意力（自注意力），把这个过程重复做
次，结果拼接起来，最后得到一个
#card=math&code=n%C3%97%28hdv%29&id=GuN5N) 的序列。
%0A%5C%5C%0A%7BMultiHead%7D(Q%2C%20K%2C%20V)%20%3D%7BConcat%7D(%7Bhead%7D%7B1%7D%2C%20%5Ccdots%2C%20%7Bhead%7D%7Bh%7D)%0A#card=math&code=%7Bhead%7D%7Bi%7D%20%3D%20%7BAttention%7D%28Q%20W%7Bi%7D%5E%7BQ%7D%2C%20K%20W%7Bi%7D%5E%7BK%7D%2C%20V%20W%7Bi%7D%5E%7BV%7D%29%0A%5C%5C%0A%7BMultiHead%7D%28Q%2C%20K%2C%20V%29%20%3D%7BConcat%7D%28%7Bhead%7D%7B1%7D%2C%20%5Ccdots%2C%20%7Bhead%7D_%7Bh%7D%29%0A&id=LiufK)
其中，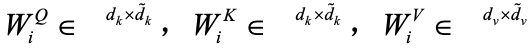
对应线性变换的权重矩阵。
前馈神经网络FFN
得到的序列经过残差连接和层级归一化（Layer Normalization）层，然后被送入一个前馈神经网络中进行降维处理。前馈神经网络包含两个线性变换和一个非线性ReLU激活函数，计算公式如下：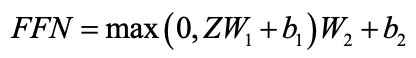
其中，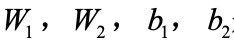
是可训练的参数。
Transformer QA
Q：为什么加入 Positional Embedding？
A：Attention机制与CNN结构一样，无法表示文本的时序型，因此相比于LSTM结构，在NLP领域效果要差一些，而加入位置信息，相当于给予了时序特性。
Q：为什么不把K和Q用同一个值了？
A：我们知道K和Q的点乘是为了得到一个attention score 矩阵，用来对V进行提纯。K和Q使用了不同的W_k, W_Q来计算，可以理解为是在不同空间上的投影。正因为有了这种不同空间的投影，增加了表达能力，这样计算得到的attention score矩阵的泛化能力更高。
Q：attention为啥需要scaled（为什么除以dk的平方根）
官方解释：向量的点积结果会很大，将softmax函数push到梯度很小的区域，scaled会缓解这种现象。怎么理解将sotfmax函数push到梯度很小区域？还有为什么scaled是维度的根号，不是其他的数？
A1：QK进行点积之后，值之间的方差会较大，也就是大小差距会较大。在数量级相差较大时，softmax将几乎全部的概率分布都分配给了最大值对应的标签。从而导致softmax的梯度消失为0，造成参数更新困难。
A2：选择根号
是因为可以使得
的结果满足期望为0，方差为1的分布，也就有效地控制了前面提到的梯度消失的问题，类似于归一化。
Q：为什么Transformer 需要进行 Multi-head Attention？
A：分为多个头，形成多个子空间，每个头关注不同方面的信息。
Transformer的多头注意力看上去是借鉴了CNN中同一卷积层内使用多个卷积核的思想，head彼此之间参数不共享，最终将结果拼接起来，这样可以允许模型在不同的表示子空间里学习到相关的信息。简而言之，就是希望每个注意力头，只关注最终输出序列中一个子空间，互相独立。其核心思想在于，抽取到更加丰富的特征信息。
Q：为什么要将multi-head attention的输入和输出相加？
A：类似于resnet中的残差学习单元，有ensemble的思想在里面，解决网络退化问题
Q：为什么multi-head attention后面要加一个ffn？
A：类比cnn网络中，cnn block和fc交替连接，效果更好。相比于单独的multi-head attention，在后面加一个ffn，可以提高整个block的非线性变换的能力。
参考
若有收获，就点个赞吧
0 人点赞
