转载自《CRF条件随机场的原理、例子、公式推导和应用》
代码实现可以参考《手撕 BiLSTM-CRF》、《简明条件随机场CRF介绍（附带纯Keras实现）》
一、CRF基础
1、无向图
2、马尔可夫随机场
什么是场？什么是随机过程？
什么是随机场？什么是马尔可夫随机场？
二、CRF原理
1、条件随机场
2001年，John Lafferty, Andrew McCallum 和 Fernando Pereira，在论文《 Conditional Random fields ：Probabilistic Models for Segmenting and Labeling Sequence Data》提出条件随机场。
条件随机场定义如下：
2、线性链条件随机场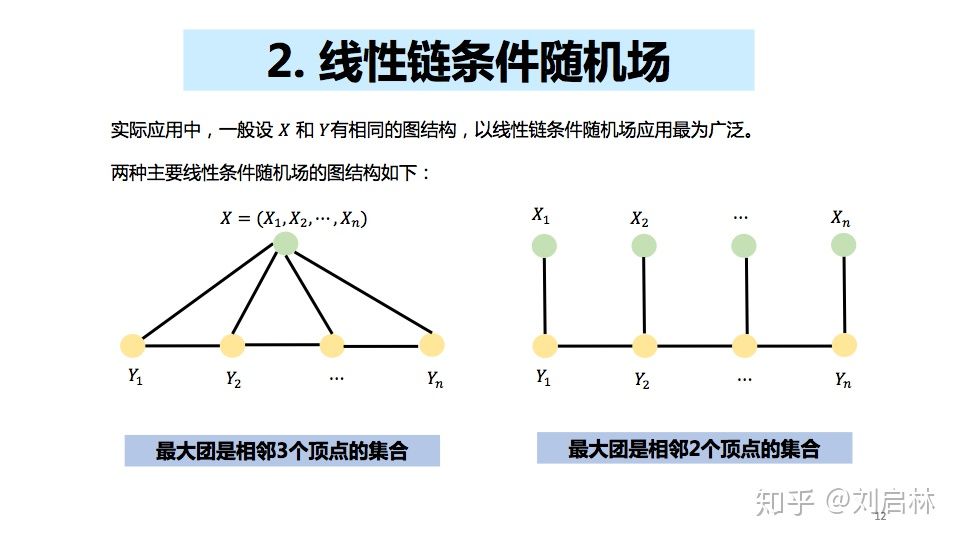
线性链条件随机场的定义如下：
线性链条件随机场CRF的图结构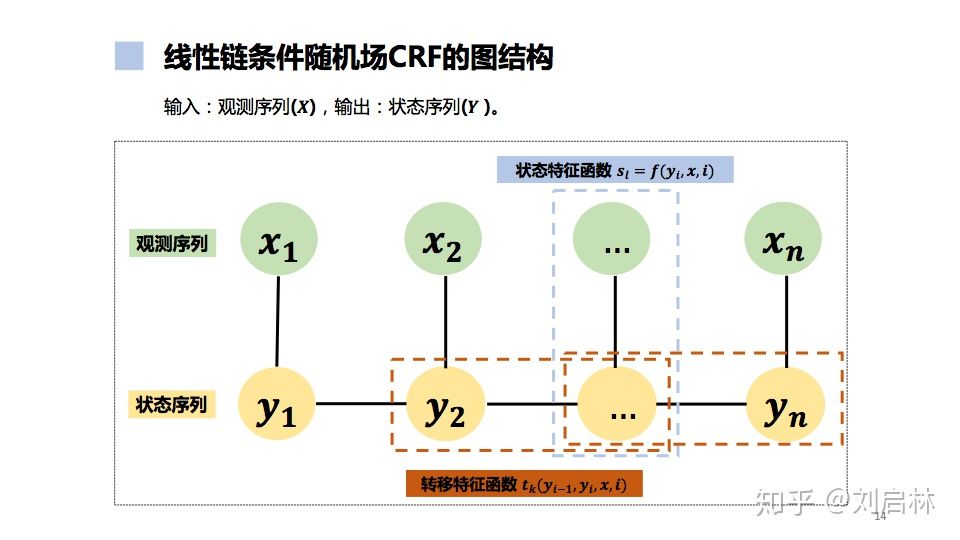
3、线性链条件随机场公式
特征函数定义如下：
三、CRF公式
参考自 Overview of Conditional Random Field (CRF) 、简明条件随机场CRF介绍（附带纯Keras实现）
为了简单起见，将转移特征和状态特征及其权值用统一符号表示。条件随机场简化公式如下：
%3D%5Cfrac%7B1%7D%7BZ(x)%7D%20%5Cexp%20%5Csum%7Bk%3D1%7D%5E%7BK%7D%20w%7Bk%7D%20f%7Bk%7D(y%2C%20x)%0A#card=math&code=P%28y%20%5Cmid%20x%29%3D%5Cfrac%7B1%7D%7BZ%28x%29%7D%20%5Cexp%20%5Csum%7Bk%3D1%7D%5E%7BK%7D%20w%7Bk%7D%20f%7Bk%7D%28y%2C%20x%29%0A&id=Fi77P)
其中，
#card=math&code=Z%28x%29&id=WEApX)是归一化因子：
%3D%5Csum%7By%E2%88%88Y%7D%20%5Cexp%20%5Cleft(%5Csum%7Bk%3D1%7D%5E%7BK%7D%20w%7Bk%7D%20f%7Bk%7D(y%2C%20x)%5Cright)%0A#card=math&code=Z%28x%29%3D%5Csum%7By%E2%88%88Y%7D%20%5Cexp%20%5Cleft%28%5Csum%7Bk%3D1%7D%5E%7BK%7D%20w%7Bk%7D%20f%7Bk%7D%28y%2C%20x%29%5Cright%29%0A&id=GDl8v)
，
是打分函数（满足马尔科夫假设，即只需要对每一个标签和每一个相邻标签对分别打分，然后将所有打分结果求和得到总分）
%3D%5Cunderbrace%7BP%5Cleft(y%7Bi%7D%20%5Cmid%20y%7Bi-1%7D%5Cright)%7D%7B%5Ctext%20%7BPrior%20%7D%7Bi%7D%7D%2B%5Cunderbrace%7BP%5Cleft(y%7Bi%7D%20%5Cmid%20x%7Bi%7D%5Cright)%7D%7B%5Ctext%20%7BLikelihood%20%7D%7Bi%7D%7D%0A#card=math&code=f%5Cleft%28y%7Bi-1%7D%2C%20y%7Bi%7D%2C%20x%7Bi%7D%5Cright%29%3D%5Cunderbrace%7BP%5Cleft%28y%7Bi%7D%20%5Cmid%20y%7Bi-1%7D%5Cright%29%7D%7B%5Ctext%20%7BPrior%20%7D%7Bi%7D%7D%2B%5Cunderbrace%7BP%5Cleft%28y%7Bi%7D%20%5Cmid%20x%7Bi%7D%5Cright%29%7D%7B%5Ctext%20%7BLikelihood%20%7D_%7Bi%7D%7D%0A&id=keH48)
其中 
#card=math&code=P%28y%7Bi%7D%20%5Cmid%20y%7Bi-1%7D%29&id=N7ZS4) 表示transition概率， 
#card=math&code=P%28y%7Bi%7D%20%5Cmid%20x%7Bi%7D%29&id=TUsKH) 表示emission概率（likelihood）
归一化因子
为了训练CRF模型，我们用最大似然方法(即，最小化负对数似然)，也就是用
%0A#card=math&code=-%5Clog%20P%5Cleft%28y%7B1%7D%2C%20%5Cldots%2C%20y%7Bn%7D%20%5Cmid%20x%5Cright%29%0A&id=z99g8)
作为损失函数，可以算出它等于
%2B%5Csum%7Bt%3D1%7D%5E%7Bn-1%7D%5Cleft%5Bg%5Cleft(y%7Bt%7D%2C%20y%7Bt%2B1%7D%5Cright)%2Bh%5Cleft(y%7Bt%2B1%7D%20%3B%20%5Cboldsymbol%7Bx%7D%5Cright)%5Cright%5D%5Cright)%2B%5Clog%20Z(%5Cboldsymbol%7Bx%7D)%0A#card=math&code=-%5Cleft%28h%5Cleft%28y%7B1%7D%20%3B%20%5Cboldsymbol%7Bx%7D%5Cright%29%2B%5Csum%7Bt%3D1%7D%5E%7Bn-1%7D%5Cleft%5Bg%5Cleft%28y%7Bt%7D%2C%20y%7Bt%2B1%7D%5Cright%29%2Bh%5Cleft%28y_%7Bt%2B1%7D%20%3B%20%5Cboldsymbol%7Bx%7D%5Cright%29%5Cright%5D%5Cright%29%2B%5Clog%20Z%28%5Cboldsymbol%7Bx%7D%29%0A&id=ws6U5)
其中第一项是原来概率式的分子的对数，它目标的序列的打分，虽然它看上去挺迂回的，但是并不难计算。真正的难度在于分母的对数
#card=math&code=logZ%28x%29&id=V3AHe)这一项，指数量级为（
），因此直接来算几乎是不可能的。
幸运的是，在CRF模型中，由于我们只考虑了临近标签的联系（马尔可夫假设），因此我们可以使用动态规划递归地算出归一化因子，使得原来是指数级的计算量降低为线性级别。
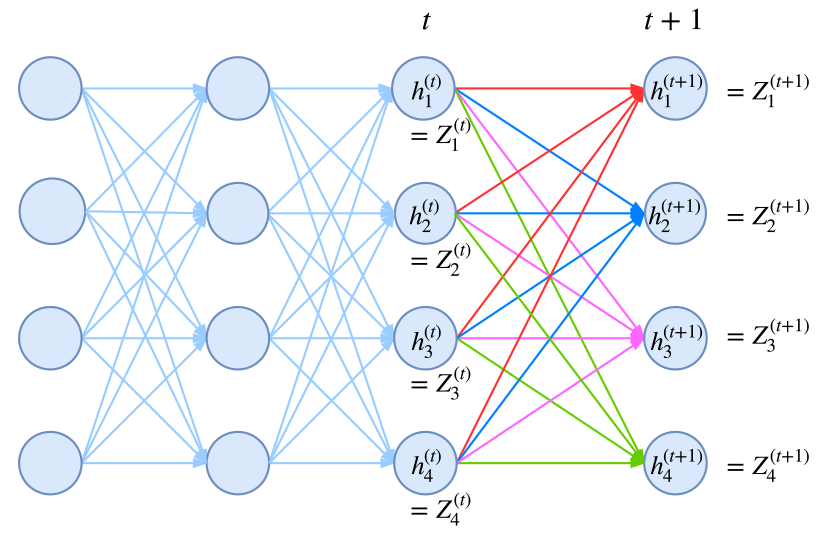
归一化因子的递归计算图示。从t到t+1时刻的计算，包括转移概率和j+1节点本身的概率
CRF Inference
模型训练完成后，如何根据输入推理找出最优路径来。跟前面一样，这也是一个从 
条路径中选最优的问题，而同样地，因为马尔可夫假设的存在，它可以转化为一个动态规划问题，用viterbi算法解决，计算量正比于n。
四、CRF总结
1、CRF的概括总结
CRF的
2、图模型之间的关系
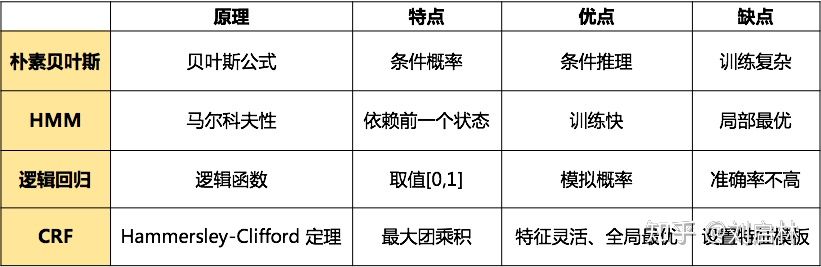
朴素贝叶斯、HMM、逻辑回归、CRF等图模型关系如下：
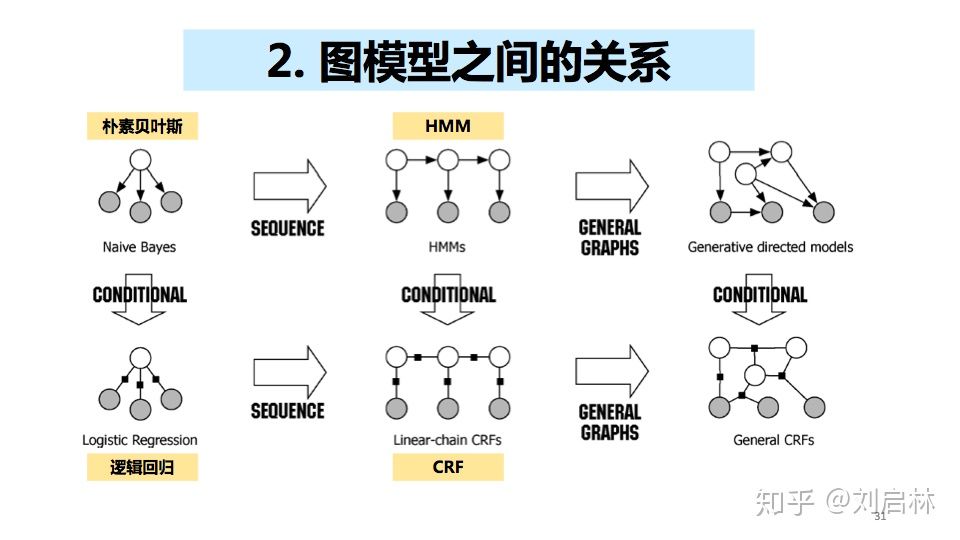朴素贝叶斯、HMM、逻辑回归、CRF对比如下表所示：
