2022-06-23-k近邻法

k近邻方法 (k-Nearest Neighbor，KNN) 是一种惰性学习算法，可以用于回归和分类，它的主要思想是投票机制，对于一个测试实例, 我们在有标签的训练数据集上找到和最相近的k个样本，用他们的label进行投票，分类问题则进行表决投票，回归问题使用加权平均或者直接平均的方法。 在 K=3 的分类任务中，由于 3 个最相似的标记示例的多数票，未标记的数据点被标记为粉红色

算法和模型

输入:训练数据%2C(x_2%2Cy_2)%2C…%2C(x_N%2Cy_n)%5C%7D%0A#card=math&code=T%3D%5C%7B%28x_1%2Cy_1%29%2C%28x_2%2Cy_2%29%2C…%2C%28x_N%2Cy_n%29%5C%7D%0A&id=tfYem)，其中是实例的特征向量，表示类别，
输出: 实例x所属的类别y

由于这个模型很容易理解，我们直接给出kNN分类模型其算法伪代码步骤：

1. 根据跟定的距离度量的方法，在T中找到和x最邻近的k个点，记作x的邻域#card=math&code=N_k%28x%29&id=v75jW)
2. 对于分类问题，在#card=math&code=N_k%28x%29&id=peKOs)中使用多数表决规则：

%7DI(yi%3Dc_j)%0A#card=math&code=y%3Dargmax%7Bcj%7D%20%5Csum%7Bx_i%20%5Cin%20N_k%28x%29%7DI%28y_i%3Dc_j%29%0A&id=Ni9l6)

1. 对于回归问题，得到y

%7Dyi%0A#card=math&code=y%3D%20%5Cfrac%7B1%7D%7Bk%7D%20%5Csum%7Bx_i%20%5Cin%20N_k%28x%29%7Dy_i%0A&id=KyOXd)
其中.

从上述算法中，我们可以看到，kNN没有显示的训练和学习模型的过程，这是一个惰性的学习方法，主要有两个点需要我们关注，一个是距离的度量；另一个是超参数k值的选择，接下来我们就来考虑这两个问题。

距离的度量

我们刚才提到KNN的一个关键点就是如何度量距离，对于两个向量#card=math&code=%28x_i%2C%20x_j%29&id=hqHlz),一般使用距离进行计算。

假设特征空间是n维实数向量空间, 其中，,
%7D%2Cx_i%5E%7B(2)%7D%2C…%2Cx_i%5E%7B(n)%7D)%EF%BC%8Cx_j%3D(x_j%5E%7B(1)%7D%2Cx_j%5E%7B(2)%7D%2C…%2Cx_j%5E%7B(n)%7D)#card=math&code=x_i%3D%28x_i%5E%7B%281%29%7D%2Cx_i%5E%7B%282%29%7D%2C…%2Cx_i%5E%7B%28n%29%7D%29%EF%BC%8Cx_j%3D%28x_j%5E%7B%281%29%7D%2Cx_j%5E%7B%282%29%7D%2C…%2Cx_j%5E%7B%28n%29%7D%29&id=nxWgh)， 则的距离定义为:

%20%3D%20%5Cleft(%20%5Csum%7Bl%3D1%7D%5E%7Bn%7D%7Cx_i%5E%7B(l)%7D-x_j%5E%7B(l)%7D%7C%5Ep%20%5Cright)%20%5E%20%7B%5Cfrac%7B1%7D%7Bp%7D%7D%0A#card=math&code=L_p%28x_i%2Cx_j%29%20%3D%20%5Cleft%28%20%5Csum%7Bl%3D1%7D%5E%7Bn%7D%7Cxi%5E%7B%28l%29%7D-x_j%5E%7B%28l%29%7D%7C%5Ep%20%5Cright%29%20%5E%20%7B%5Cfrac%7B1%7D%7Bp%7D%7D%0A&id=gbczk)

这里的. 当p=2时候，称为欧氏距离(Euclidean distance), 有

%20%3D%20%5Cleft(%20%5Csum%7Bl%3D1%7D%5E%7Bn%7D%7Cxi%5E%7B(l)%7D-x_j%5E%7B(l)%7D%7C%5E2%20%5Cright)%20%5E%20%7B%5Cfrac%7B1%7D%7B2%7D%7D%0A#card=math&code=L_2%28x_i%2Cx_j%29%20%3D%20%5Cleft%28%20%5Csum%7Bl%3D1%7D%5E%7Bn%7D%7Cxi%5E%7B%28l%29%7D-x_j%5E%7B%28l%29%7D%7C%5E2%20%5Cright%29%20%5E%20%7B%5Cfrac%7B1%7D%7B2%7D%7D%0A&id=lxbIN)

当p=1时候，称为曼哈顿距离(Manhattan distance), 有

%20%3D%20%5Csum%7Bl%3D1%7D%5E%7Bn%7D%7Cxi%5E%7B(l)%7D-x_j%5E%7B(l)%7D%7C%20%0A#card=math&code=L_1%28x_i%2Cx_j%29%20%3D%20%5Csum%7Bl%3D1%7D%5E%7Bn%7D%7Cxi%5E%7B%28l%29%7D-x_j%5E%7B%28l%29%7D%7C%20%0A&id=qxuOn)

当时候，称为极大距离(infty distance), 表示各个坐标的距离最大值， 有

%20%3D%20%5Cmax%7Bl%7D%7Bn%7D%7Cxi%5E%7B(l)%7D-x_j%5E%7B(l)%7D%7C%0A#card=math&code=L_p%28x_i%2Cx_j%29%20%3D%20%5Cmax%7Bl%7D%7Bn%7D%7Cx_i%5E%7B%28l%29%7D-x_j%5E%7B%28l%29%7D%7C%0A&id=Y4gmS)

使用距离计算的时候，我们一般使用欧氏距离，一般情况下都是将数据转化成实数向量的形式，使用距离度量方式，找到最近的k个值，进行投票打分.

k值的选择

kNN中的k是一个超参数，需要我们进行指定。这个k和数据有很大关系，一般通过交叉验证进行选择，但是建议使用交叉验证的时候，, 使用交叉验证得到一个很好的k值。

• 一种流行的方法是测试不同大小的“k”并测量产生的误差，找出“肘点”作为最佳K值（在该值处增加会导致误差和的减小非常小，而减小会急剧增加误差和）

附录：kd 树

kNN，从上述算法中，我们可以看到主要是从训练数据中，知道k个相近实例，但是每次都要遍历这个数据集合，主要的问题就是速度慢. 这时候就出现了加速查找的数据结构，其中之一就是kd 树.

构造kd 树
kd树是一种对k维空间中的实例进行存储以便能够进行快速检索的数据结构. kd树是一个二叉树，表示对k维空间的一个划分. 构造kd树就是不断用垂直于坐标轴的超平面 (一般用每一个维度的中位数来表示) 将k维空间划分，构成一系列的k维超矩形区域.

伪代码: (from wikipedia)

function kdtree (list of points pointList, int depth)
{
    // Select axis based on depth so that axis cycles through all valid values
    var int axis := depth mod k;
    // Sort point list and choose median as pivot element
    select median by axis from pointList;
    // Create node and construct subtree
    node.location := median;
    node.leftChild := kdtree(points in pointList before median, depth+1);
    node.rightChild := kdtree(points in pointList after median, depth+1);
    return node;
}

基于kd树查找最近邻
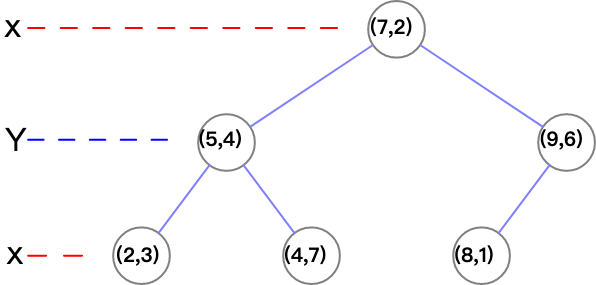
构造kd树的目的就是快速查找最近邻和k近邻，给定数据 T = {(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}，根据x维度有{2,4,5,7,8,9}: 中位数是7，因此(7,2)作为根节点，x < 7,在左子树，其他在右子树。依次递归构造左右子树，下一次根据维度y，之后根据维度x. 注意这里的k是维度，n 可能大学k，故要每次对k取余数. （这个k不是kNN中的k）.

总结

kNN简单好用，但是最主要的是这个思想，多数投票加权平均。kd树只是一种加速的方法，还有kd平衡树，ball tree等，这也是一种思想，并不是准则。KNN和kd tree的代码稍后便到。