title: 经典算法重温 Aho-Corasick automaton（转载）
subtitle: 经典算法重温 Aho-Corasick automaton（转载）
date: 2020-12-01
author: NSX
catalog: true
tags:
- Aho-Corasick
- AC自动机

转载自：经典算法—Aho-Corasick automaton

Aho–Corasick automaton 算法（简称AC自动机）是由Alfred V. Aho和Margaret J.Corasick于1975年在贝尔实验室发明的多模(模式串)匹配算法。即给定多个模式串和一个文本串，求解多模串在文本串中存在的情况(包括是否存在、存在几次、存在于哪些位置等)。

单模匹配

在介绍AC自动机这种多模匹配算法前，先回顾下单模匹配问题，即给定一个文本串和一个模式串，求解模式串在文本串中的匹配情况。

1.1 朴素匹配

最直接的想法是暴力(Brute Force)匹配，即将文本串的第一个字符与模式串的第一个字符进行匹配，若相等则继续比较文本串的第二个字符与模式串的第二个字符。若不等，则比较目标串的第二个字符与模式串的第一个字符，依次比较下去，直到得到最后的匹配结果。相关代码如下：

  1. # 每次匹配失败时，文本串T的指针回退到开始匹配位置的下一个位置，模式串P的指针回退到初始位置，然后重新开始匹配
  2. def bfMatch(T,P):
  3.     tLen,pLen = len(T),len(P)
  4.     indexs = []
  5.     for i in range(tLen - pLen + 1):
  6.         for j in range(pLen):
  7.             if T[i+j] == P[j]:
  8.                 if j == pLen - 1:
  9.                     indexs.append(i)
  10.                 continue
  11.             break
  12.     return indexs
  14. T='ushershe' 
  15. P='he' 
  16. print(bfMatch(T,P))

上述匹配过程存在重复匹配，KMP算法优化了上述匹配过程。在匹配失败时，文本串的指针不需要回退。

1.2 KMP算法

与朴素匹配不同，KMP算法在匹配到某个字符失败时，文本串的匹配指针不会回退，模式串则根据部分匹配表(也叫next数组) 向右滑动一定距离后继续与上次在文本串中不匹配的位置进行匹配，若仍不匹配，则继续根据部分匹配表向右滑动模式串，重复上述不匹配–滑动的过程，当匹配指针指到模式串的初始位置依然不匹配，则模式串向右滑动一位，文本串的匹配指针向前移动一位；若匹配，则继续匹配其他位置的字符。当匹配指针连续匹配的字符数与模式串的长度相等，则匹配完成。形象图解可参考字符串匹配的KMP算法。相应代码为：

  1. # 匹配过程中，模式串P中每个待匹配的字符与文本串T中的字符对齐，即匹配指针相同，但两个字符串的下标不同
  2. # 部分匹配表是针对模式串构建的
  3. def kmpMatch(T,P):
  4.     tLen,pLen = len(T),len(P)
  5.     Next = partialMatchTable(P)
  6.     q = 0 # 模式串P的下标
  7.     indexs = []
  8.     for i in range(tLen):
  9.         while q > 0 and P[q] != T[i]:
  10.             q = Next[q-1]
  11.         if P[q] == T[i]:
  12.             q += 1
  13.         if q == pLen:
  14.             indexs.append(i-pLen+1)
  15.             q=0
  16.     return indexs

部分匹配表中的数值是指某个子串的前缀和后缀的最长共有元素的长度。 其有两种构建方式。一种是手动法，详见字符串匹配的KMP算法。相关代码如下：

  1. # 手动法求部分匹配表
  2. def partialMatchTable(p): # 也叫next数组
  3.     prefix,suffix = set(),set()
  4.     pLen = len(p)
  5.     Next = [0]
  6.     for i in range(1,pLen):
  7.         prefix.add(p[:i]) 
  8.         suffix = {p[j:i+1] for j in range(1,i+1)}
  9.         common_len = len((prefix & suffix or {''}).pop())
  10. #         print(p[:i+1],prefix,suffix,common_len)
  11.         Next.append(common_len) 
  12.     return Next
  14. p='ababaca'
  15. partialMatchTable(p)

另一种是程序法，模式串针对自己的前后缀的匹配。详见KMP算法：线性时间O(n)字符串匹配算法中的部分匹配表部分。相关代码如下：

  1. # 由模式串生成的部分匹配表，其存储的是前缀尾部 的位置。有前缀尾部 = next(后缀尾部)，
  2. # 当后缀之后q不匹配时，通过查询部分匹配表，确定前缀尾部的位置k,然后将前缀滑动过来与后缀对齐，继续后续匹配工作
  3. # 程序法计算部分匹配表 
  4. def partialMatchTable(p):
  5.     pLen = len(p)
  6.     Next = [0]
  7.     k = 0 # 模式串nP的下标
  8.     for q in range(1,pLen): # 文本串nT的下标
  9.         while k > 0 and p[k] != p[q]:
  10.             k = Next[k-1]
  11.         if p[k] == p[q]:
  12.             k += 1
  13.         Next.append(k)
  14.     return Next
  16. p='ababaca'
  17. partialMatchTable(p)

多模匹配

给定多个模式串和一个文本串，求解多模串在文本串中存在的情况(包括是否存在、存在几次、存在于哪些位置等)。

2.1 Trie

Trie又叫前缀树或字典树，是一种多叉树结构。Trie这个术语来源于retrieval(检索)，其是一种用于快速检索的数据结构。其核心思想是利用字符串的公共前缀最大限度地减少不必要的字符串比较，提高查询(检索)效率，缺点是内存消耗大。

Trie树的基本性质：

  • 根节点不包含字符，除根节点外的每一个子节点都包含一个字符
  • 从根节点到某一个节点，路径上经过的字符连起来为该节点对应的字符串
  • 每个节点的所有子节点包含的字符互不相同

应用场景

  • 前缀匹配(自动补全)：返回所有前缀相同的字符串
  • 词频统计：将每个节点是否构成单词的标志位改成构成单词的数量
  • 字典序排序：将所有待排序集合逐个加入到Trie中，然后按照先序遍历输出所有值
  • 分词
  • 检索

2.2 AC自动机

有了上述KMP和Trie的背景知识后，对AC自动机会有更加清晰的认识。

AC自动机首先将将模式串预处理为确定有限状态自动机(与Trie树的构建类似)，然后按照文本串中的字符顺序依次接收字符，并发生状态转移。状态中缓存了如下三种情况下的跳转与输出：

  1. 按字符转移成功，但不是模式串的结尾。即成功转移到另一个状态，对应success表/goto表；
  2. 按字符转移成功，是模式串的结尾。即命中一个模式串，对应emits/output；
  3. 按字符转移失败，此时跳转到一个特定的节点，对应failure。从根节点到这个特定的节点的路径恰好是失败前的文本的一部分，类似KMP算法中利用部分匹配表来加速模式串的滑动从而减少重复匹配

上述匹配过程只需扫描一遍文本串，其时间复杂度为O(n)，与模式串的数量和长度无关。

AC自动机可简单看成是在Trie树上通过KMP来实现多模串的匹配。其中Trie树负责状态转移，KMP负责减少重复匹配。一个常见的例子就是给出n个单词，再给出一段包含m个字符的文章，让你找出有多少个单词在文章里出现过。 简单地讲，AC自动机就是字典树+kmp算法+失配指针。Python 库 ahocorasick 封装了 AC 自动机，简单易用，而且解决了 UTF-8 字符编码问题。

  1. import ahocorasick
  3. patterns = ['中国', '山东省', '威海市', '山东大学', '威海校区'] # 词典
  4. text = '山东大学威海校区坐落于美丽滨城威海市。'
  6. trie = ahocorasick.Automaton()
  7. for index, word in enumerate(patterns):
  8.     trie.add_word(word, (index, word))
  9. trie.make_automaton()
  11. for each in trie.iter(text):
  12.     print(each)

PS：更多pyahocorasick API方法可以参考《ahocorasick documentation》

补充：AC自动机基本构造

以经典的ushers为例，模式串是he、she、his、hers，文本为“ushers”。构建的自动机如图：

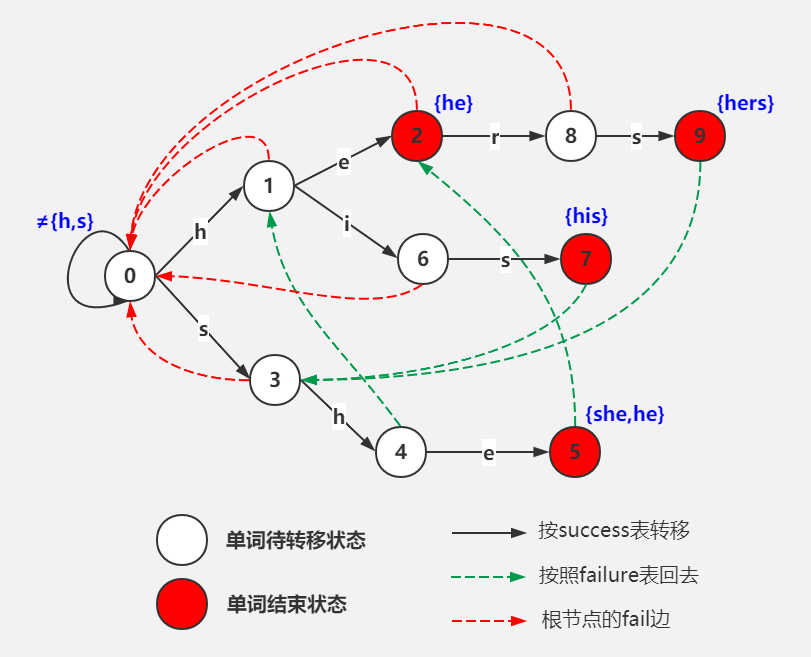
image.png

其中实线部分是一颗Trie树，虚线部分为各节点的fail路径。

匹配过程

自动机从根节点0出发

  1. 首先尝试按success表转移（图中实线）。按照文本的指示转移，也就是接收一个u。此时success表中并没有相应路线，转移失败。
  2. 失败了则按照failure表回去（图中虚线）。按照文本指示，这次接收一个s，转移到状态3。
  3. 成功了继续按success表转移，直到失败跳转步骤2，或者遇到output表中标明的“可输出状态”（图中红色状态）。此时输出匹配到的模式串，然后将此状态视作普通的状态继续转移。

算法高效之处在于，当自动机接受了“ushe”之后，再接受一个r会导致无法按照success表转移，此时自动机会聪明地按照failure表转移到2号状态，并经过几次转移后输出“hers”。来到2号状态的路不止一条，从根节点一路往下，“h→e”也可以到达。而这个“he”恰好是“ushe”的结尾，状态机就仿佛是压根就没失败过（没有接受r），也没有接受过中间的字符“us”，直接就从初始状态按照“he”的路径走过来一样（到达同一节点，状态完全相同）。

AC自动机的构建虽然与Trie树的构建类似，但其fail路径(本质是一种回溯，避免重复匹配)是AC自动机中特有的。goto表、output 表、failure 表的具体构建逻辑可参考《Aho-Corasick算法的Java实现与分析-hankcs》

参考