梯度下降法详解

梯度下降的直观解释

首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

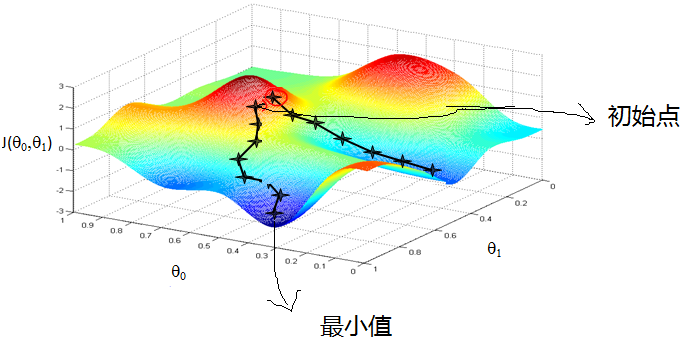
所以，什么是梯度下降呢？对于人来说，我们是很容易知道那条路径下降最快的，可是机器却不是那么聪明的。他们只能靠算法，找到这个最快下降的路径。这个算法，就是我们所说的梯度下降了。

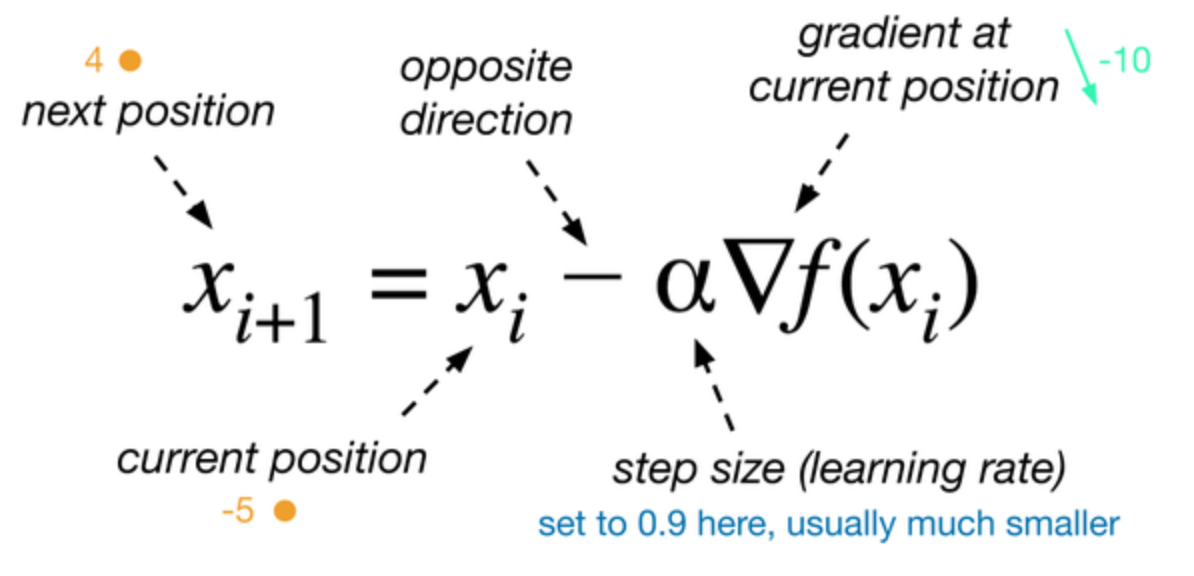
梯度下降是一种最小化目标函数的方法，目标函数对模型参数的梯度为，梯度下降就是沿着梯度的反方向更新参数，学习率定义了我们达到（局部）最小值期间的步幅。换句话说，我们是在目标函数创造的陡坡上顺坡向下走，直到谷底。

梯度下降的详细算法

1. 先决条件：确认优化模型的假设函数和损失函数。对于线性回归，假设函数为，损失函数为
2. 算法相关参数初始化: 𝜃 向量可以初始化为默认值，或者调优后的值。算法终止距离𝜀，步长 𝛼 初始化为1
3. 算法过程：
   1. 确定当前位置的损失函数的梯度，对于𝜃向量，其梯度表达式为
   2. 用步长乘以损失函数的梯度，得到当前位置下降的距离，即对应于前面登山例子中的某一步
   3. 确定𝜃向量里面的每个值，如果梯度下降的距离都小于𝜀，则算法终止，当前𝜃向量即为最终结果。否则进入下一个步骤
   4. 更新𝜃向量，其更新表达式。更新完毕后继续转入步骤1.

梯度下降法分类

《3 Types of Gradient Descent Algorithms for Small & Large Data Sets》

基于如何使用数据计算代价函数的导数，梯度下降法可以被定义为不同的形式（various variants）。确切地说，根据使用数据量的大小（the amount of data），时间复杂度（time complexity）和算法的准确率（accuracy of the algorithm），梯度下降法可分为：

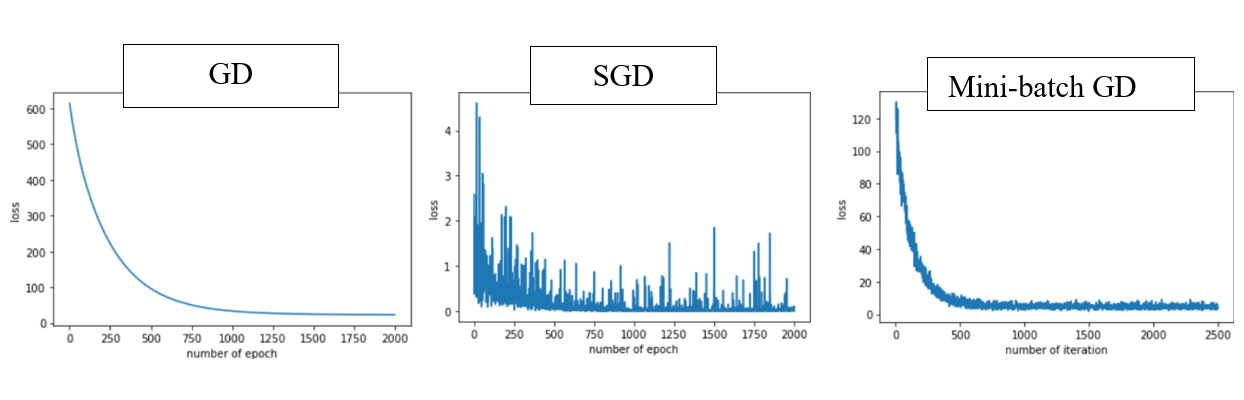
1. 批量梯度下降法（Batch Gradient Descent, GD）
2. 随机梯度下降法（Stochastic Gradient Descent, SGD）
3. 小批量梯度下降法（Mini-Batch Gradient Descent, Mini-Batch GD）

1.批梯度下降

批量梯度下降（batch gradient descent），是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来对参数 θ 进行更新：

由于我们有m个样本，这里求梯度的时候就用了所有m个样本的梯度数据。这肯定是能找到最优的下降方向，但是同时也造成了计算量过大，时间过长的后果。

写成代码的话，BGD大概形式如下：

for i in range(nb_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params = params - learning_rate * params_grad

2.随机梯度下降

随机梯度下降法（stochastic gradient descent，SGD），其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是在每次迭代仅选择一个训练样本和标签去计算代价函数的梯度，然后更新参数：

随机梯度下降法，和4.1的批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

那么，有没有一个中庸的办法能够结合两种方法的优点呢？有！这就是接下来的小批量梯度下降法。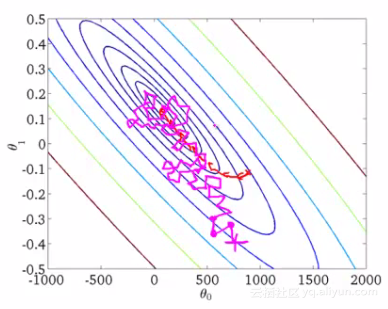

随机梯度下降法不像批量梯度下降法那样收敛，而是游走到接近全局最小值的区域终止

代码上，就是简单在训练样本上加了层循环，并用每个样本计算梯度。注意这里每轮训练都对数据做了混淆，原因见下文。

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

3.最小批梯度下降

小批量梯度下降法是最广泛使用的一种算法，而且用最小批的时候一般也会用术语 SGD 进行指代。对于m个样本，最小批梯度下降每次采样 n 个训练样本（称之为一批）来对参数 θ 进行更新：

每次使用批数据, 虽然不能反映整体数据的情况, 不过却很大程度上加速了 NN 的训练过程, 而且也不会丢失太多准确率。通过这种方式，

1. 降低参数更新时的变化（降低方差），能够更加稳定地收敛；
2. 可以利用尖端深度学习库中常见的、高度优化过的矩阵最优化技术，高效计算小批数据的梯度。

伪代码示例如下：

for i in range(nb_epochs):
  np.random.shuffle(data)
  for batch in get_batches(data, batch_size=50):
    params_grad = evaluate_gradient(loss_function, batch, params)
    params = params - learning_rate * params_grad

参考

梯度下降与优化综述-明月轩
梯度下降（Gradient Descent）小结