什么是 Trie 树

Trie 树，又称前缀树，字段典树，或单词查找树，是一种树形结构，也是哈希表的变种，它是一种专门处理字段串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题，主要被搜索引擎用来做文本词频的统计。

先看一下前辍树的图：

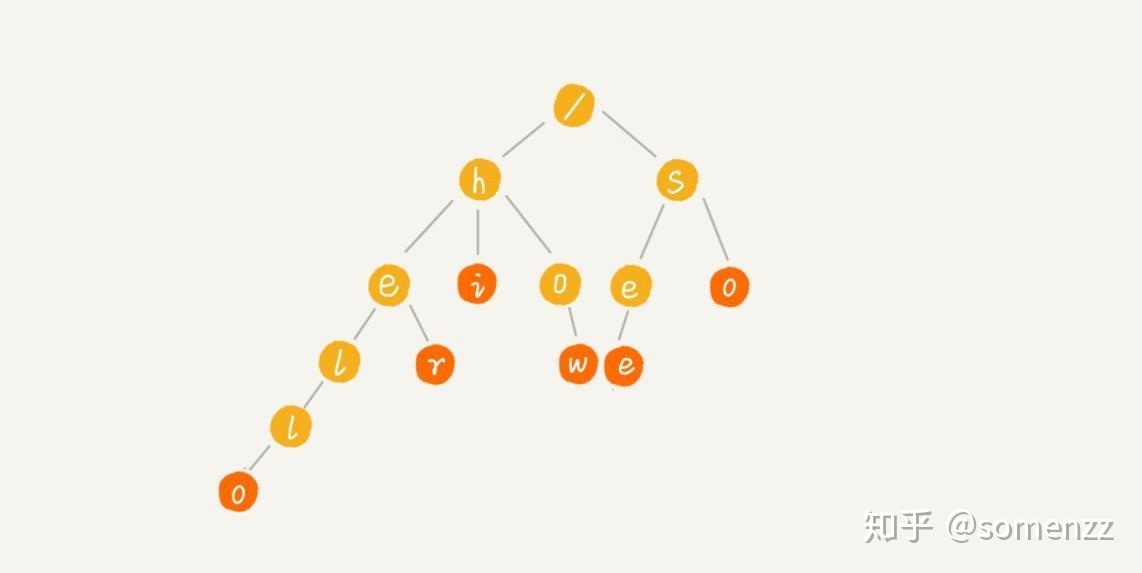
2022-02-11-Trie 树实现搜索引擎自动联想 - 图1

这棵前辍树根节点不存放数据，其他节点保存了 hello,her,hi,how,see,so 等关键词信息，如果查 he 前辍的单词可以很快返回 hello,her。

Trie 树的 Python 实现

一般来讲 trie 要实现这么几个方法

  • 插入一个单词 insert (word: str) -> None
  • 查找一个单词是否在 trie 中 search (word:str) -> bool
  • 查找一个前缀是否在 trie 中 startsWith (prefix:str) -> bool
  1. class Trie:
  3.     def __init__(self):
  4.         """
  5.         Initialize your data structure here.
  6.         """
  7.         self.root = {}
  8.         self.end_of_word = '#'
  10.     def insert(self, word: str) -> None:
  11.         """
  12.         Inserts a word into the trie.
  13.         """
  14.         node = self.root
  15.         for char in word:
  16.             node = node.setdefault(char, {})
  17.         node[self.end_of_word] = self.end_of_word
  19.     def search(self, word: str) -> bool:
  20.         """
  21.         Returns if the word is in the trie.
  22.         """
  23.         node = self.root
  24.         for char in word:
  25.             if char not in node:
  26.                 return False
  27.             node = node[char]
  28.         return self.end_of_word in node
  30.     def startsWith(self, prefix: str) -> bool:
  31.         """
  32.         Returns if there is any word in the trie that starts with the given prefix.
  33.         """
  34.         node = self.root
  35.         for char in prefix:
  36.             if char not in node:
  37.                 return False
  38.             node = node[char]
  39.         return True
  41.     def get_start(self,prefix):
  42.         '''
  43.         给出一个前辍，打印出所有匹配的字符串
  44.         :param prefix:
  45.         :return:
  46.         '''
  47.         def get_key(pre,pre_node):
  48.             result = []
  49.             if pre_node.get(self.end_of_word):
  50.                 result.append(pre)
  51.             for key in pre_node.keys():
  52.                 if key != self.end_of_word:
  53.                     result.extend(get_key(pre+key,pre_node.get(key)))
  54.             return result
  57.         if not self.startsWith(prefix):
  58.             return []
  59.         else:
  60.             node = self.root
  61.             for p in prefix:
  62.                 node = node.get(p)
  63.             else:
  64.                 return get_key(prefix,node)
  66. if __name__ == "__main__":
  67.     trie = Trie()
  68.     trie.insert("Python")
  69.     trie.insert("Python 算法")
  70.     trie.insert("Python web")
  71.     trie.insert("Python web 开发")
  72.     trie.insert("Python web 开发 视频教程")
  73.     trie.insert("Python 算法 源码")
  74.     trie.insert("Perl 算法 源码")
  75.     print(trie.search("Perl"))
  76.     print(trie.search("Perl 算法 源码"))
  77.     print((trie.get_start('P')))
  78.     print((trie.get_start('Python web')))
  79.     print((trie.get_start('Python 算')))
  80.     print((trie.get_start('P')))
  81.     print((trie.get_start('Python web')))
  82.     print((trie.get_start('Python 算')))

代码运行结果如下：

  1. False
  2. True
  3. ['Python', 'Python 算法', 'Python 算法 源码', 'Python web', 'Python web 开发', 'Python web 开发 视频教程', 'Perl 算法 源码']
  4. ['Python web', 'Python web 开发', 'Python web 开发 视频教程']
  5. ['Python 算法', 'Python 算法 源码']

Trie 的时间复杂度

如果要在一组关键词中，频繁地查询某些关键词，用 Trie 树会非常高效。构建 Trie 树的过程，需要扫描所有的关键词，时间复杂度是 O(n)（n 表示所有关键词的长度和）。但是一旦构建成功之后，后续的查询操作会非常高效。

每次查询时，如果要查询的关键词长度是 k，那我们只需要最多比对 k 个节点，就能完成查询操作。跟原本那组关键词的长度和个数没有任何关系。所以说，构建好 Trie 树后，在其中查找关键词的时间复杂度是 O(k)，k 表示要查找的关键词的长度。

Trie三方实现库

自己造轮子还要思考，编码，验证，但这是学习提升的最佳方式。如果急于应用没有时间造轮子，至少要学会如何使用轮子，下面的前辍树的轮子是一个日本人写的，大家可以学习应用下。

https://github.com/pytries/marisa-trie

https://marisa-trie.readthedocs.io/en/latest/tutorial.html

参考