layout: post
title: 常见距离度量方法
subtitle: 常见距离度量方法
date: 2021-11-09
author: NSX
header-img: img/post-bg-ios9-web.jpg
catalog: true
tags:
- 距离度量
在NLP中,我们经常要去比较两个句子的相似度,其标准方法是想办法将句子编码为固定大小的向量(Word2Vec、BERT等),然后用某种几何距离(欧氏距离、cos距离等)作为相似度。这种方案相对来说比较简单,而且检索起来比较快速,一定程度上能满足工程需求。
数值向量距离💡
1. 闵可夫斯基距离(Minkowski distance)
闵氏距离不是一种距离,而是一组距离的定义,将以下形式的距离都定义为Minkowski distance。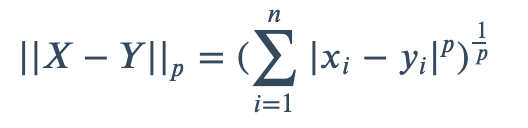
1.1 曼哈顿距离(Manhattan/cityblock distance)
曼哈顿距离(L1范数/Manhattan Distance) 在欧几里得空间的固定直角坐标系上,两点所形成的线段对轴产生的投影的距离总和( 如棋盘 )。它们只能移动直角,且计算距离时不涉及对角线的移动。
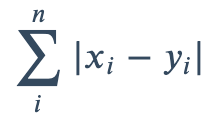
numpy实现
import numpy as npdef Manhattan(vec1, vec2):return np.sum(np.abs(dataA - dataB))# return np.linalg.norm(vec1-vec2,ord=1)# return 1/(1+np.sqrt((np.sum(vec1-vec2)**2)))
scipy中的距离计算模块
from scipy.spatial import distancex = [5, 3, 9]y = [0, 1, 6]dis = distance.cityblock(x, y)print(dis)
1.2 欧氏距离(Euclidean distance)
欧氏距离(L2范数/欧几里得度量/Euclidean Distance)指在m维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离)。计算公式为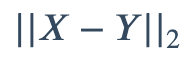
二维空间中的欧氏距离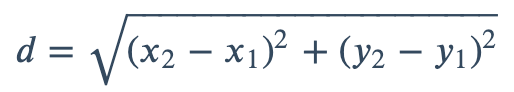
三维空间中的欧式距离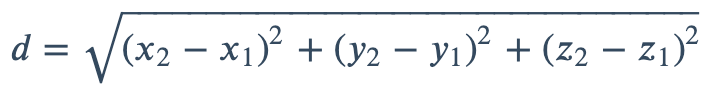
n维空间中的欧式距离
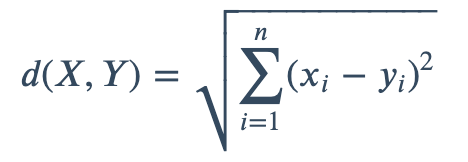
- numpy实现
```python import numpy as np
def EuclideanDistance(vec1, vec2): d = 1.0/(1.0 + np.linalg.norm(vec1-vec2, ord=2))
# d = 1.0/(1.0 + np.sqrt(np.sum(np.square(vec1-vec2))))
- scipy实现```pythonfrom scipy.spatial import distancey = [0, 1, 0]dis = distance.euclidean(x, y)print(dis)
1.3 切比雪夫距离(Chebyshev distance)
切比雪夫距离(Chebyshev distance)是向量空间中的一种度量,二个点之间的距离定义是其各坐标数值差绝对值的最大值。以数学的观点来看,切比雪夫距离是由一致范数(uniform norm)(或称为上确界范数)所衍生的度量,也是超凸度量(injective metric space)的一种。计算公式为
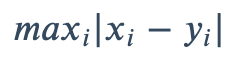
- scipy实现
from scipy.spatial import distancex = [5, 3, 9]y = [0, 1, 6]dis = distance.chebyshev(x, y)print(dis)
2. 马氏距离(Mahalanobis distance)
协方差矩阵记为𝑆,则马式距离为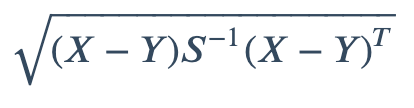
若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式就成了欧氏距离了!
3. 夹角余弦距离(Cosine distance)
余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1,而其他任何角度的余弦值都不大于1;并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时,余弦相似度的值为1;两个向量夹角为90°时,余弦相似度的值为0;两个向量指向完全相反的方向时,余弦相似度的值为-1。这结果是与向量的长度无关的,仅仅与向量的指向方向相关。余弦相似度通常用于正空间,因此给出的值为0到1之间。
余弦相似度定义来自于欧几里得点积,点积定义如下: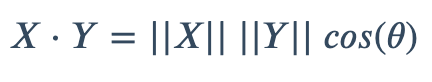
余弦相似度为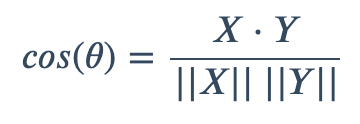
numpy实现
def Cosine(vec1, vec2):sumData = np.dot(vec1, vec2) # = np.sum(dataA*dataB)denom = np.linalg.norm(vec1) * np.linalg.norm(vec2)return 0.5 + 0.5 * (sumData / denom) # 归一化 [0,1]
numpy实现(矩阵形式输入)
def Cosine(s1_vec_ist, s2_vec_list):_matrixA = np.array(s1_vec_ist)_matrixB = np.array(s2_vec_list)_matrixA_matrixB = np.dot(_matrixA, _matrixB.transpose())_matrixA_norm = np.sqrt(np.multiply(_matrixA, _matrixA).sum(axis=1))_matrixB_norm = np.sqrt(np.multiply(_matrixB, _matrixB).sum(axis=1))similar_scores = np.divide(_matrixA_matrixB, _matrixA_norm * _matrixB_norm.transpose())similar_scores = 0.5 + 0.5 * similar_scores[0]
scipy实现
x = [5, 3, 9]y = [0, 1, 6]dis = distance.cosine(x, y)print(dis)
sklearn实现 ```python import numpy as np from sklearn.metrics.pairwise import cosine_similarity, paired_distances
simi = cosine_similarity(x, y) simi = [x[0] for x in dot_list]
- Keras实现```pythondef consine_distance(vectors):(featsA, featsB) = vectorsdis = K.sum(featsA * featsB, axis=1, keepdims=True) / (K.sum(featsA ** 2, axis=1, keepdims=True)* K.sum(featsB ** 2, axis=1, keepdims=True))return dis
4. 修正余弦相似度
修正cosine 减去的是对item i打过分的每个user u,其打分的均值
- numpy实现 ``` data = np.mat([[1,2,3],[3,4,5]]) avg = np.mean(data[:,0]) # 下标0表示正在打分的用户
def AdjustedCosine(dataA,dataB,avg): sumData = (dataA - avg) (dataB - avg).T # 若列为向量则为 dataA.T dataB denom = np.linalg.norm(dataA - avg) np.linalg.norm(dataB - avg) return 0.5 + 0.5 (sumData / denom)
print(AdjustedCosine(data[0,:],data[1,:],avg))
<a name="PjS4l"></a>### 5. 相关系数距离(Correlation distance)<a name="PwVfc"></a>#### 5.1 Pearson相关系数- **皮尔逊相关系数(r)**,是衡量两个变量_X_和_Y之间_**线性相关性**的统计量。它的值介于 +1 和 -1 之间。+1 完全正线性相关,0 是无线性相关,-1 是完全负线性相关。- 重要推论:皮尔逊相关性只能评估两个连续变量之间的线性相关(仅当一个变量的变化与另一个变量的比例变化相关时,关系才是线性的)- **Pearson相关性系数**计算如下: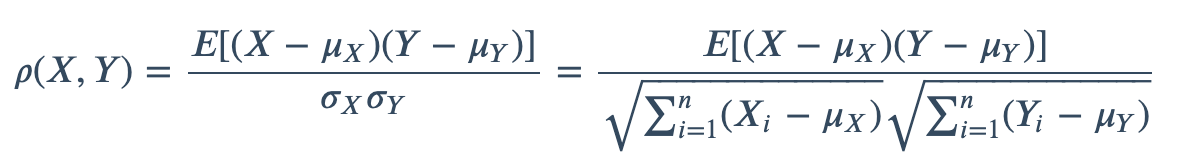<a name="tc0eh"></a>#### 5.2 Spearman系数- Spearman系数是**排序相关性(ranked values)的非参数度量**。**使用单调函数**描述两个变量之间的关系的程度- 重要推论:Spearman ρ 相关性可以评估两个变量之间的单调关系——有序,它基于每个变量的排名值(ranked value)而不是原始数据(original value)。如 orginal value(1,3,5,8,20,30,...) => ranked value (1,2,3,4,5,6...)- Spearman的计算公式如下:-  表示两个变量等级的差。Spearman的取值范围也是  ,它们的顺序完全一样时(每个 都为0)就是1,顺序完全相反时就接近于-1。**举个例子说明Spearman和Pearson的不同:**<br />假设human-score是上升的,model-score可以有如下四种情况:| 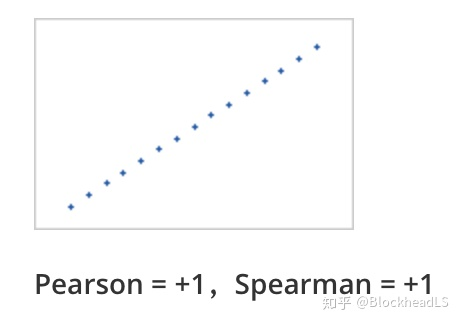 | 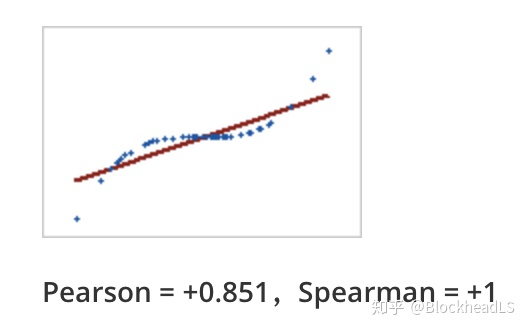 || --- | --- || 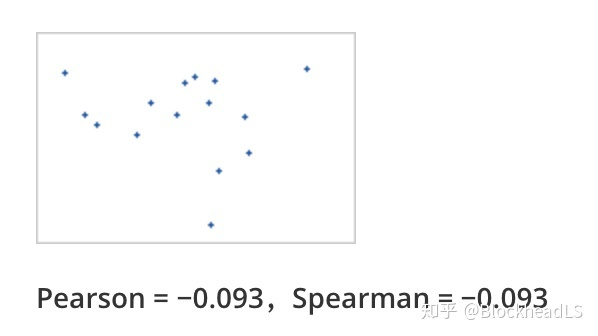 | 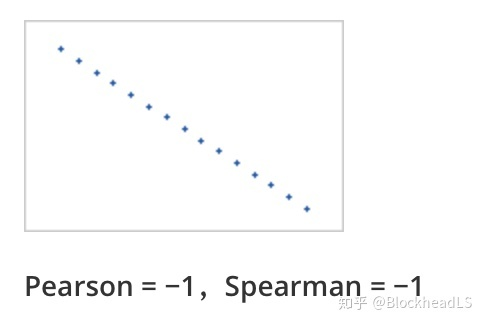 |- numpy实现```pythondef Pearson(vec1, vec2):_vec1 = vec1 - np.mean(vec1)_vec2 = vec2 - np.mean(vec2)sumData = np.dot(_vec1, _vec2)denom = np.linalg.norm(_vec1) * np.linalg.norm(_vec2)return 0.5 + 0.5 * (sumData / denom)
numpy实现(矩阵形式输入)
def pers_sim(self, s1_vec_ist, s2_vec_list):_matrixA = np.array(s1_vec_ist)_matrixB = np.array(s2_vec_list)avgA = np.mean(_matrixA)avgB = np.mean(_matrixB)_matrixA = _matrixA - avgA_matrixB = _matrixB - avgB_matrixA_matrixB = np.dot(_matrixA, _matrixB.transpose())_matrixA_norm = np.sqrt(np.multiply(_matrixA, _matrixA).sum(axis=1))_matrixB_norm = np.sqrt(np.multiply(_matrixB, _matrixB).sum(axis=1))similar_scores = np.divide(_matrixA_matrixB, _matrixA_norm * _matrixB_norm.transpose())similar_scores = 0.5 + 0.5 * similar_scores[0]
scipy 实现
x = [5, 3, 9]y = [0, 1, 6]dis = distance.correlation(x, y)print(dis)
6. KL散度距离和JS散度距离
JS散度度量了两个概率分布的相似度,基于KL散度的变体,解决了KL散度非对称的问题。一般地,JS散度是对称的,其取值是0到1之间。定义如下: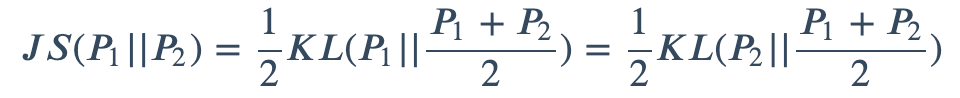
其中KL表示KL散度,KL散度又称为相对熵,信息散度,信息增益。KL散度是是两个概率分布P和Q差别的非对称性的度量。KL散度是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。典型情况下,P表示数据的真实分布,Q表示数据的理论分布,模型分布,或P的近似分布。计算公式为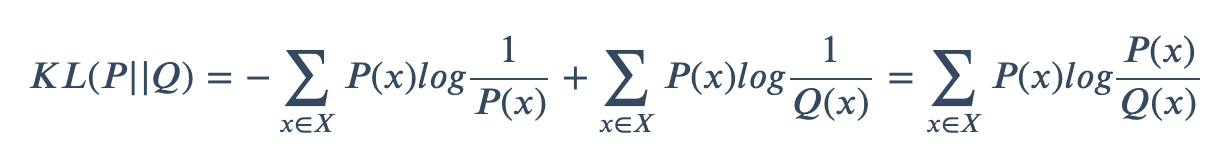
因为对数函数是凸函数,所以KL散度的值为非负数。
有时会将KL散度称为KL距离,但它并不满足距离的性质:
- KL散度不是对称的
- KL散度不满足三角不等式
KL散度和JS散度度量的时候有一个问题:
如果两个分配P,Q离得很远,完全没有重叠的时候,那么KL散度值是没有意义的,而JS散度值是一个常数。这在学习算法中是比较致命的,这就意味这这一点的梯度为0。梯度消失了。
- scipy 实现 ```python import numpy as np from scipy import stats as sts x = np.asarray([0, 2, 6]) y = np.asarray([0, 1, 6]) def JS_divergence(p, q): M = (p + q) / 2 return 0.5 sts.entropy(p, M) + 0.5 sts.entropy(q, M)
dis = JS_divergence(x, y) print(dis)
<a name="aFbYs"></a>### 7. [Wasserstein距离](https://spaces.ac.cn/archives/7388#Earth%20Mover's%20Distance)/“推土机距离”(Earth Mover's Distance,EMD)Earth Mover distance,是基于运输问题的效率提出的一种直方图相似度量。它是归一化的从一个分布变为另一个分布的最小代价, 可以用来测量两个分布之间的距离。EMD运算复杂度较高,平均而言至少是二次方级别。但是它作为距离函数,有一个非常好的特点是存在下界,两个分布的质心之间的距离,因此在粗略计算时,可以考虑用分布质心之间的距离代替EMD。<br />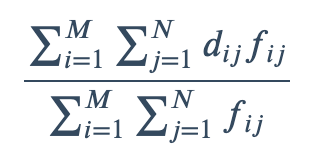- scipy 实现```pythonfrom scipy.stats import wasserstein_distancex = [3.4, 3.9, 7.5, 7.8]y = [4.5, 1.4]dis = wasserstein_distance(x, y)print(dis)
8. Word Mover’s Distance
Wasserstein距离适合于用来计算两个不同长度的序列的差异性,而我们要做语义相似度的时候,两个句子通常也是不同长度的,刚好对应这个特性,因此很自然地就会联想到Wasserstein距离也许可以用来比较句子相似度。Word Mover’s Distance(WMD)以Wasserstein距离为基础,大概可以理解为将一个句子变为另一个句子的最短路径,某种意义上也可以理解为编辑距离的光滑版。实际使用的时候,通常会去掉停用词后再计算WMD。
参考实现如下:
def word_mover_distance(x, y):"""WMD(Word Mover's Distance)的参考实现x.shape=[m,d], y.shape=[n,d]"""p = np.ones(x.shape[0]) / x.shape[0]q = np.ones(y.shape[0]) / y.shape[0]D = np.sqrt(np.square(x[:, None] - y[None, :]).mean(axis=2))return wasserstein_distance(p, q, D)
9. Word Rotator’s Distance
WMD其实已经挺不错了,但非要鸡蛋里挑骨头的话,还是能挑出一些缺点来:
1、它使用的是欧氏距离作为语义差距度量,但从Word2Vec的经验我们就知道要算词向量的相似度的话,用coscos往往比欧氏距离要好; 2、WMD理论上是一个无上界的量,这意味着我们不大好直观感知相似程度,从而不能很好调整相似与否的阈值。
为了解决这两个问题,一个比较朴素的想法是将所有向量除以各自的模长来归一化后再算WMD,但这样就完全失去了模长信息了。最近的论文《Word Rotator’s Distance: Decomposing Vectors Gives Better Representations》则巧妙地提出,在归一化的同时可以把模长融入到约束条件p,qp,q里边去,这就形成了WRD。
Word Rotator’s Distance(WRD)了。由于使用的度量是余弦距离,所以两个向量之间的变换更像是一种旋转(rotate)而不是移动(move),所以有了这个命名;同样由于使用了余弦距离,所以它的结果在[0,2][0,2]内,相对来说更容易去感知其相似程度。
参考实现如下:
def word_rotator_distance(x, y):"""WRD(Word Rotator's Distance)的参考实现x.shape=[m,d], y.shape=[n,d]"""x_norm = (x**2).sum(axis=1, keepdims=True)**0.5y_norm = (y**2).sum(axis=1, keepdims=True)**0.5p = x_norm[:, 0] / x_norm.sum()q = y_norm[:, 0] / y_norm.sum()D = 1 - np.dot(x / x_norm, (y / y_norm).T)return wasserstein_distance(p, q, D)def word_rotator_similarity(x, y):"""1 - WRDx.shape=[m,d], y.shape=[n,d]"""return 1 - word_rotator_distance(x, y)
基于字符串💡
此外,还可以直接比较两个变长序列的差异性,比如编辑距离,它通过动态规划找出两个字符串之间的最优映射,然后算不匹配程度;
基于字符串的方法都是直接对原始文本进行比较, 主要包括编辑距离[11] (Levenshtein Distance, LD)、最长公共子序列[12] (Longest Common Sequence, LCS)、N-Gram[13] 和 Jaccard 相似度[14] 等.
基于字符串的方法原理简单、实现方便, 并且直接对原始文本进行比较, 多用于文本的快速模糊匹配, 其不足主要在于没有考虑到单词的含义及单词和单词之间的相互关系, 并且同义词、多义词等问题都无法处理.
1. 汉明距离
汉明距离是一个概念,它表示两个(相同长度)字对应位不同的数量,比如:1011101 与 1001001 之间的汉明距离是 2;”toned” 与 “roses” 之间的汉明距离是 3。
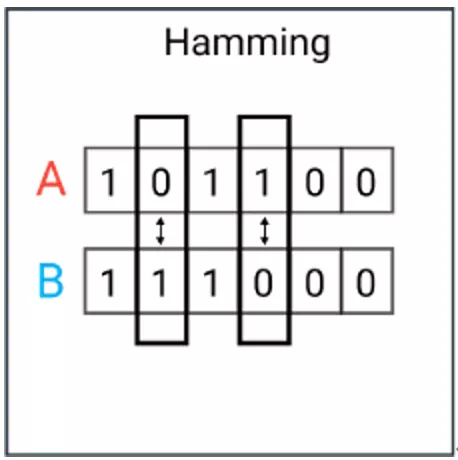
import textdistancetextdistance.hamming('text','test') #1textdistance.hamming.normalized_similarity('text','test') #0.75
- 缺点
正如你所预料的,当两个向量的长度不相等时,汉明距离很难使用。你会希望将相同长度的向量相互比较,以了解哪些位置不匹配。
而且,只要它们不同或相等,它就不考虑实际值。因此,当幅度是一个重要的衡量标准时,不建议使用这个距离衡量。 - 用例
典型的使用情况包括在计算机网络上传输数据时的纠错/检测。它可以用来确定二进制字中的失真位数,以此来估计错误。
此外,你还可以使用汉明距离来测量分类变量之间的距离。
2. Levenshtein距离
莱文斯坦距离,又称编辑距离,指两个字串之间,由一个转成另一个所需的最少编辑操作次数。其中,允许的编辑操作包括插入,删除和替换。
示例:
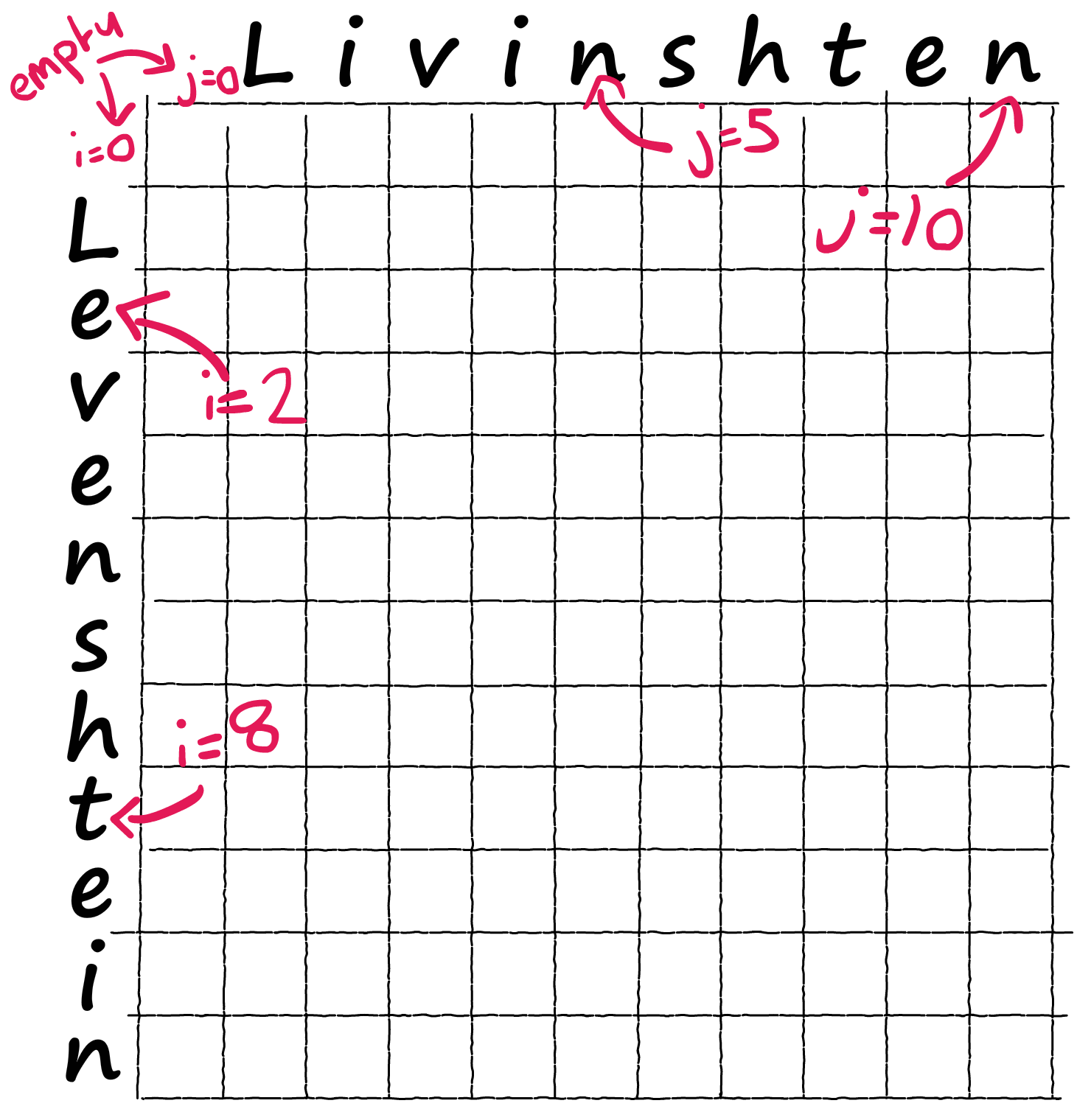 |
 |
|---|---|
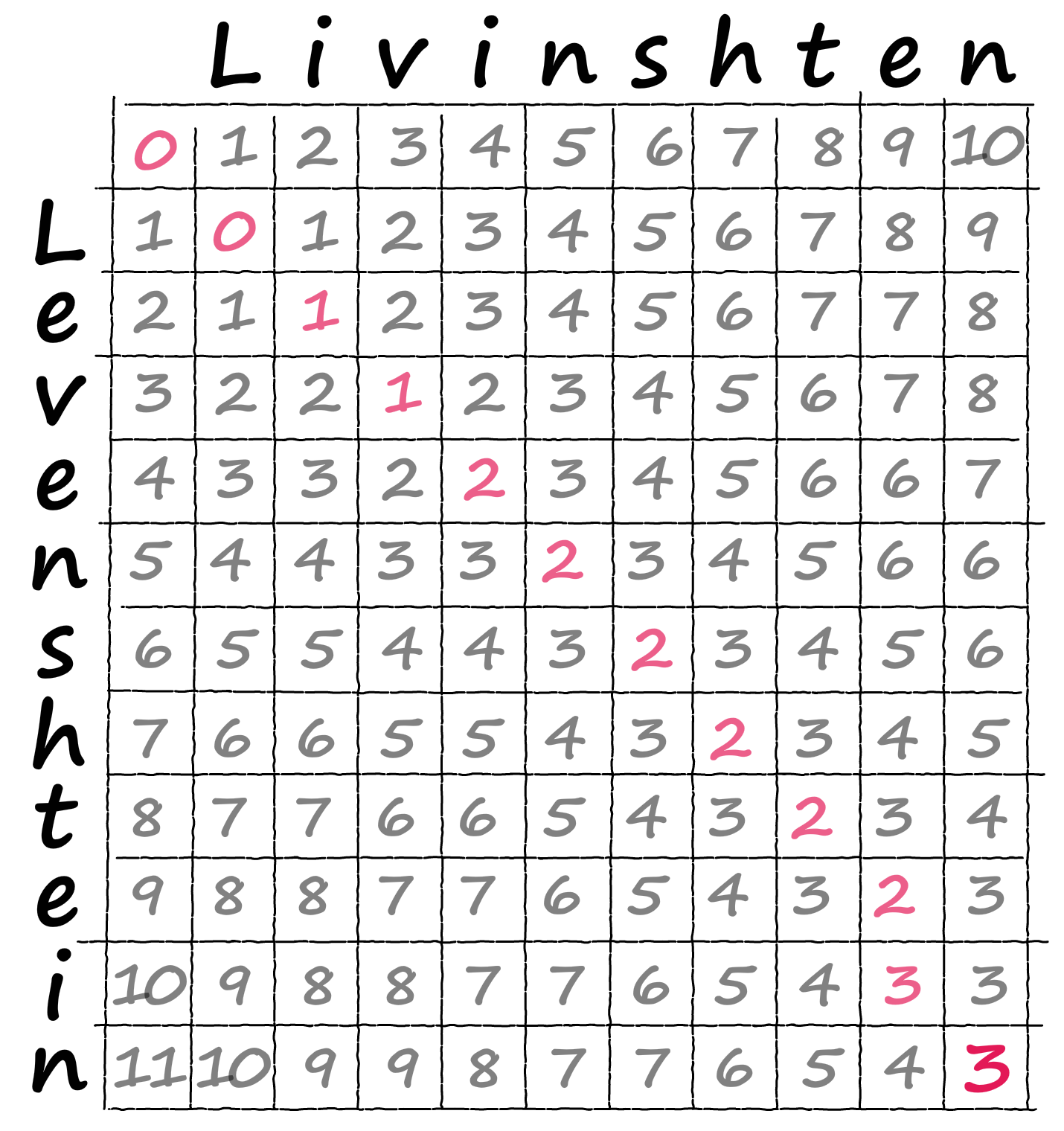
动态规划:
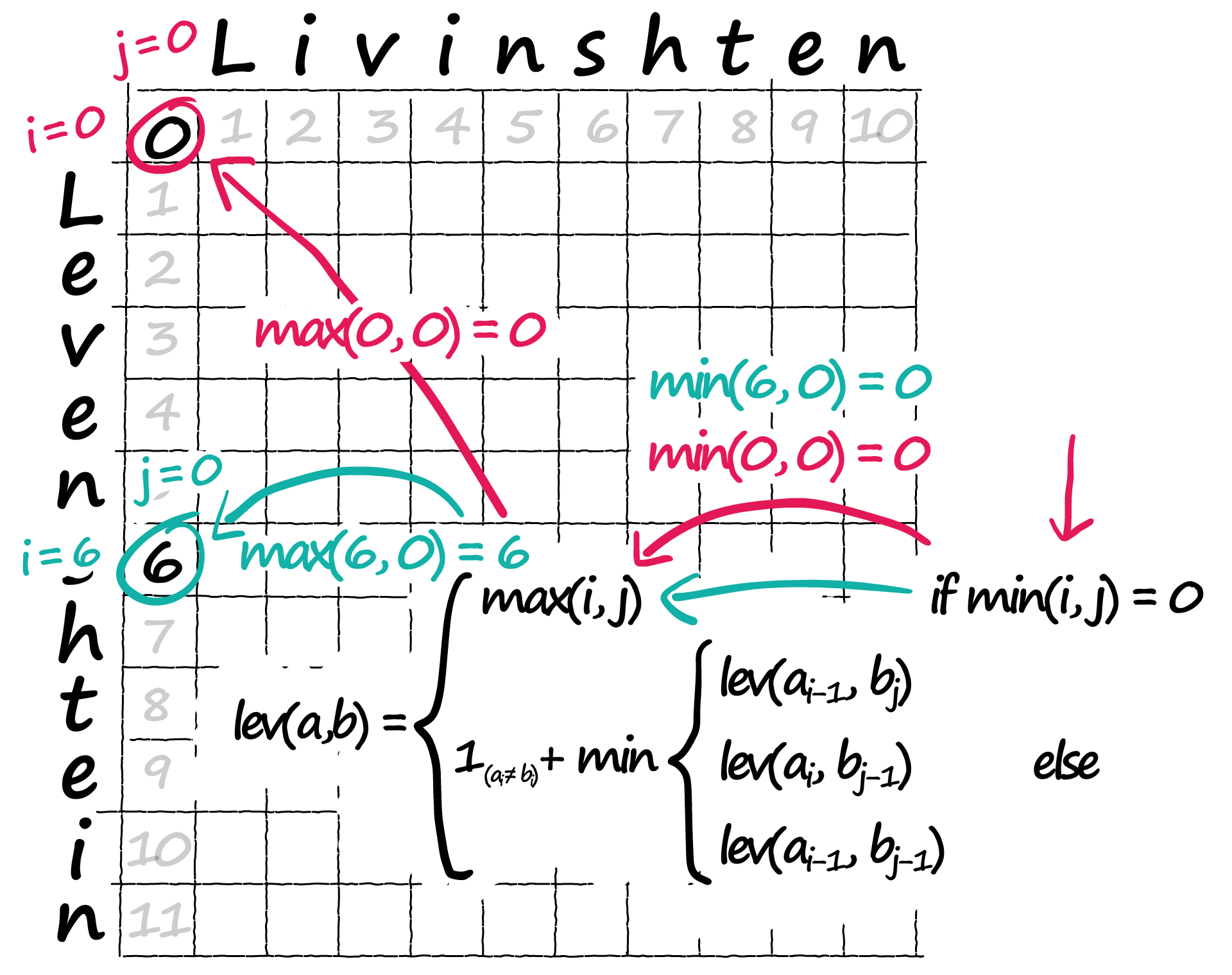 |
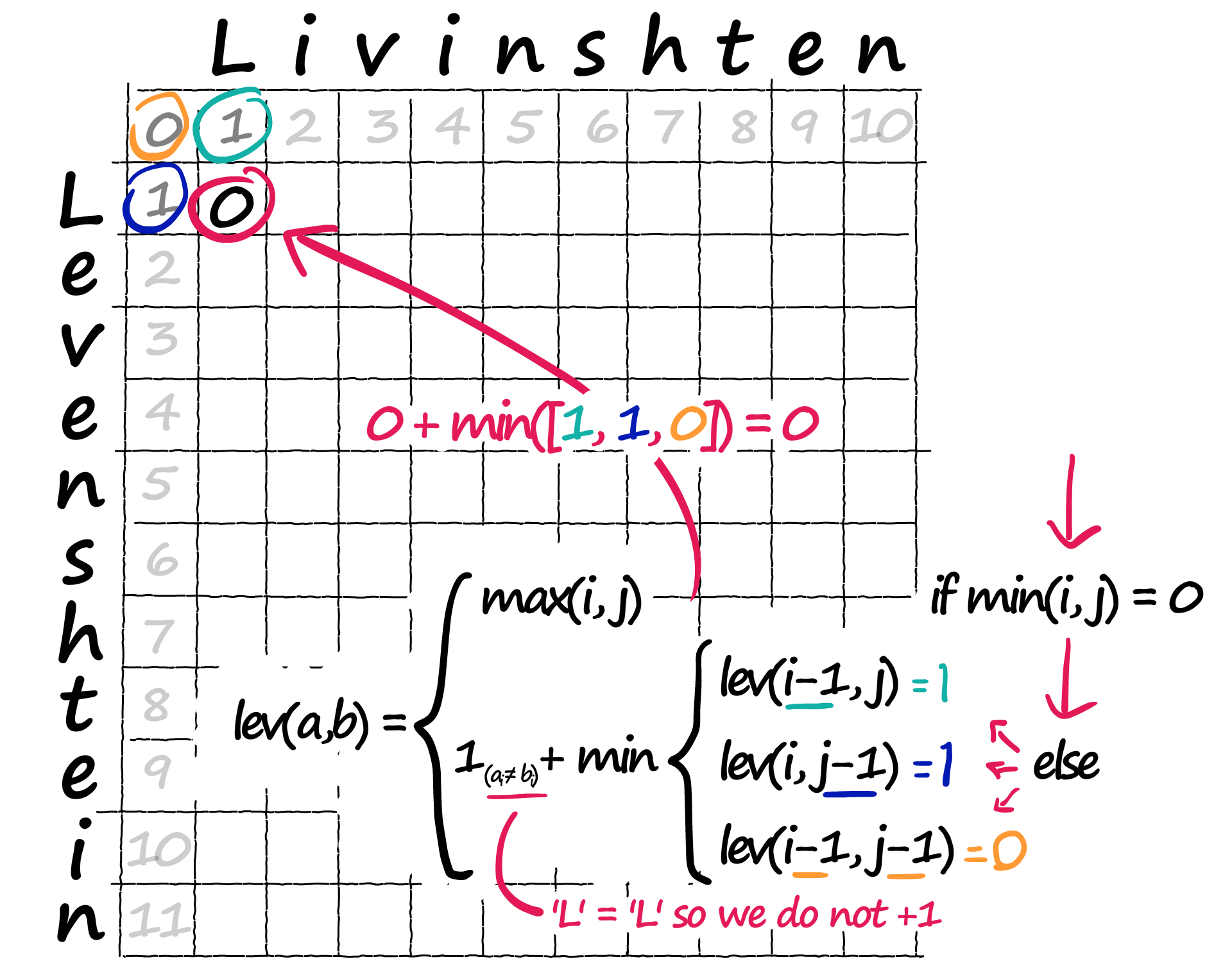 |
 |
|---|---|---|
代码:
import textdistancetextdistance.levenshtein("this test", "that test") # 2textdistance.levenshtein.normalized_similarity("this test", "that test") # 0.8
3. Jaro-Winkler距离
J-W距离(Jaro–Winkler distance)是两个字符串之间的另一个相似性度量。该算法对字符串中的字符串中的差异进行了惩罚。使用此算法的动机是,错字通常更有可能在字符串的后面而不是开头出现。比较”this test 和 test this”时,即使字符串包含完全相同的单词(只是顺序不同),相似度分数也仅为2/3。
Jaro–Winkler distance 是适合于如名字这样较短的字符之间计算相似度。0分表示没有任何相似度,1分则代表完全匹配。
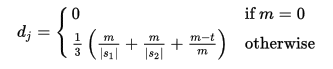
其中,m是两个字符串匹配上的字符数目,t是字符中换位数目的一半,即若在字符串的第i位出现了a,b,在第j位又出现了b,a,则表示两者出现了换位。
PS:在该算法中,更加突出了前缀相同的重要性,即如果两个字符串在前几个字符都相同的情况下,它们会获得更高的相似性。
import textdistancetextdistance.jaro_winkler("this test", "test this") # .666666666...textdistance.jaro_winkler(“ mes”,“ messi”) # 0.86
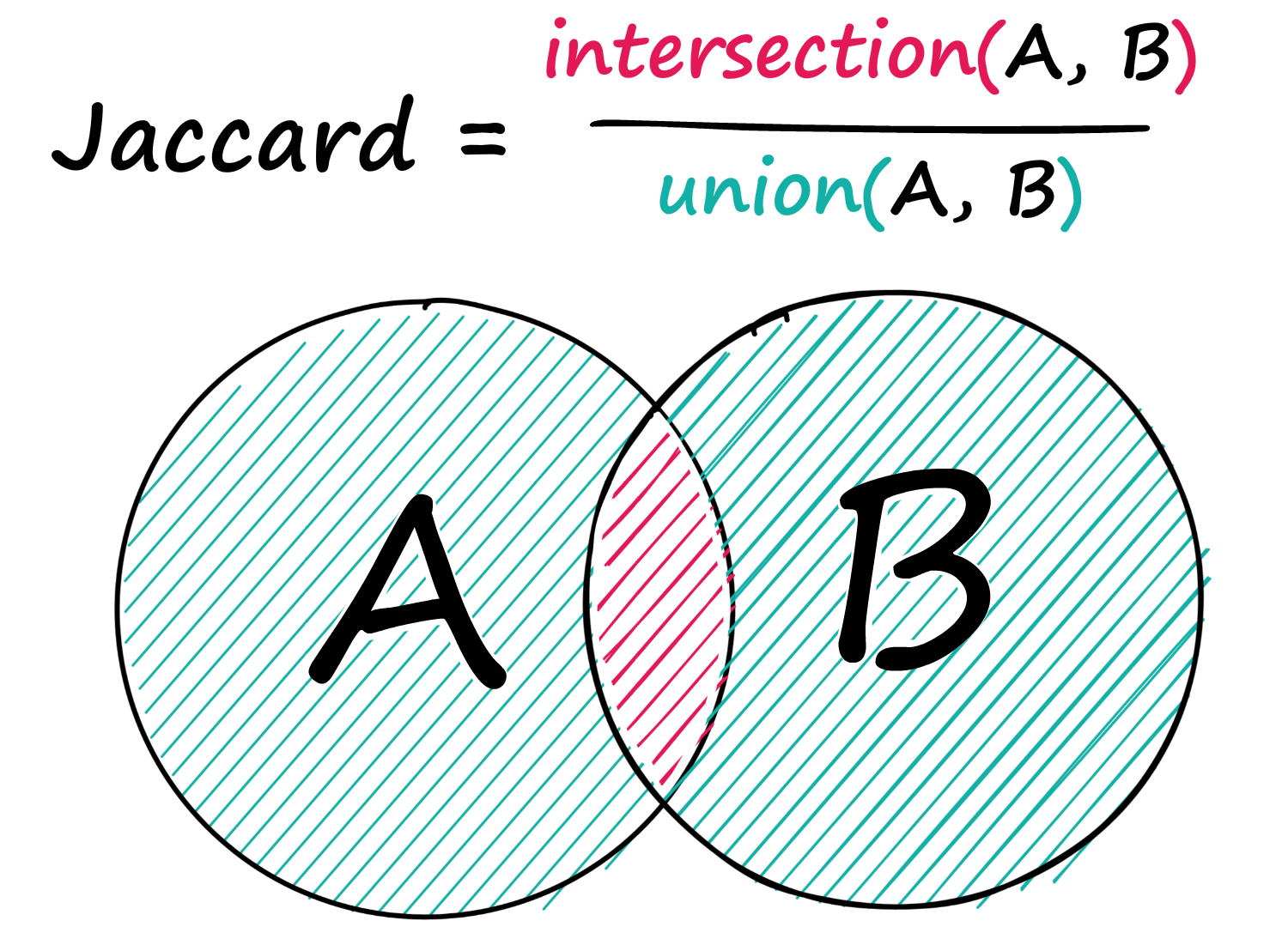
4. Jaccard 相似度
Jaccard Similarity(或称交集比联合)度量两个字符串之间的共享字符,而不考虑顺序。公式是查找公用令牌的数量并将其除以唯一令牌的总数。总结就是一句话:集合的交集与集合的并集的比例.
示例: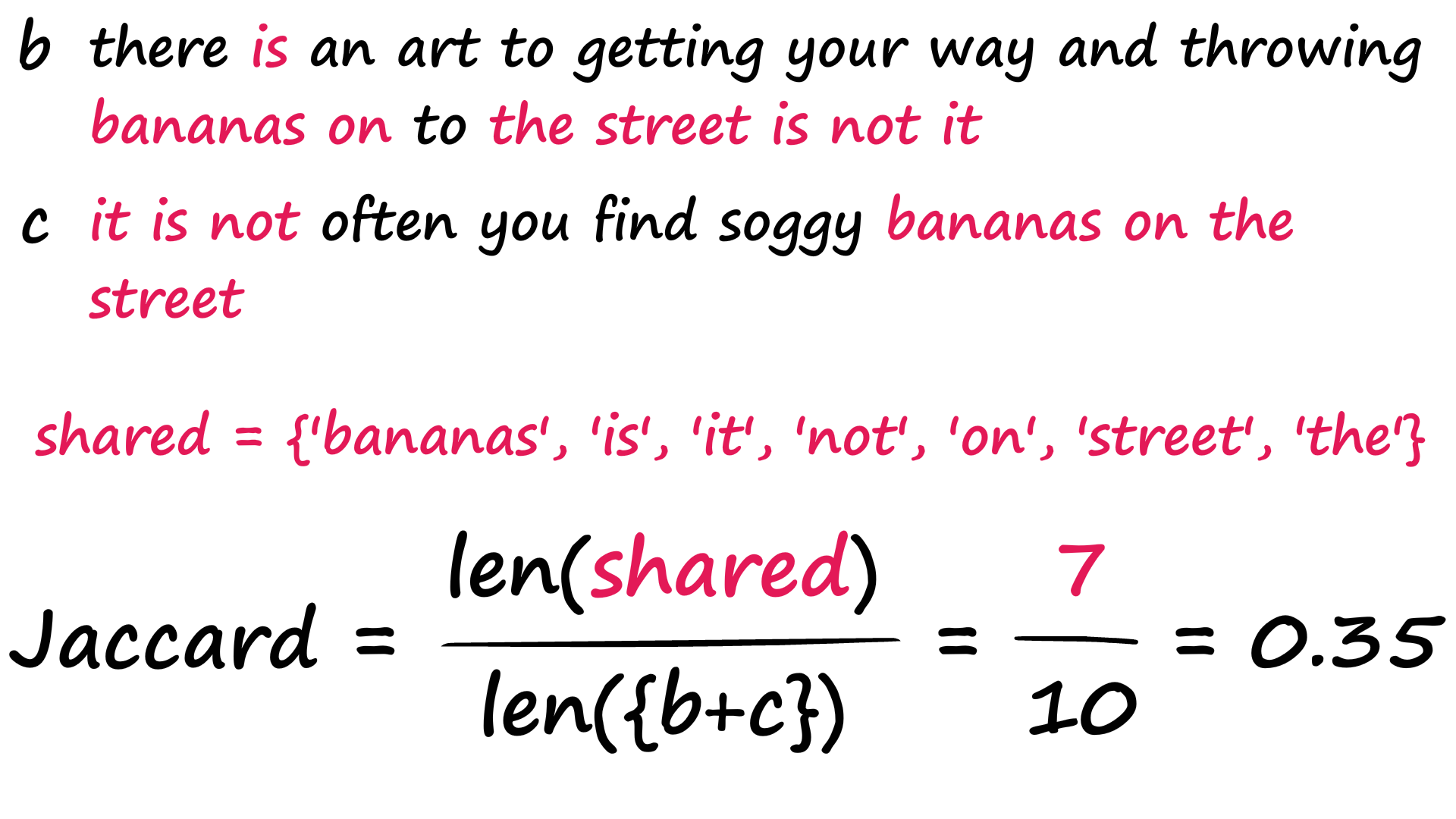
代码:
import textdistancetokens_1 =“ hello world”.split()tokens_2 =“ world hello”.split()textdistance.jaccard(tokens_1,tokens_2) #1.0tokens_1 =“ hello new world”.split()tokens_2 = “Hello World”.split()textdistance.jaccard(tokens_1,tokens_2) # 0.666
def sim_jaccard(s1, s2):"""jaccard相似度"""s1, s2 = set(s1), set(s2)ret1 = s1.intersection(s2) # 交集ret2 = s1.union(s2) # 并集sim = 1.0 * len(ret1) / len(ret2)return sim
- 缺点
Jaccard指数的一个主要缺点是,它受数据大小的影响很大。大的数据集会对指数产生很大的影响,因为它可以在保持相似的交叉点的同时显著增加联合。 - 用例
Jaccard指数经常用于使用二进制或二值化数据的应用中。当你有一个深度学习模型预测图像的片段时,例如,一辆汽车,Jaccard指数就可以用来计算给定真实标签的预测片段的准确度。同样,它也可以用于文本相似性分析,以衡量文档之间的选词重叠程度。因此,它可以用来比较模式的集合。
5. Sørensen–Dice coefficient
与 Jaccard 类似,Dice 系数也是一种计算简单集合之间相似度的一种计算方式。

import textdistancetokens_1 =“ hello world”.split()tokens_2 =“ world hello”.split()textdistance.sorensen(tokens_1,tokens_2) #1.0tokens_1 =“ hello new world”.split()tokens_2 =“ hello world”.split()textdistance.sorensen(tokens_1,tokens_2) #0.8
- 缺点
与Jaccard指数一样,它们都高估了集合的重要性,只有很少或没有TP(Truth Positive)值的正集合。因此,它可以求得多盘的平均分数。它将每个项目与相关集合的大小成反比加权,而不是平等对待它们。 - 用例
与Jaccard指数相似,通常用于图像分割任务或文本相似性分析。
6. 余弦相似度
余弦相似度是比较两个字符串的常用方法。该算法将字符串视为向量,并计算它们之间的余弦值。与上面的 Jaccard Similarity 相似,余弦相似度也忽略了要比较的字符串中的顺序。
import textdistancetextdistance.cosine("apple", "ppale") # 1.0

常用文本匹配库
textdistance 是一个用于比较两个或多个序列之间距离的Python库。它使用30多种不同的算法计算序列的距离,提供了可用于模糊匹配算法的集合.
python-Levenshtein 是一个快速计算Levenshtein距离和字符串相似度的模块。它能够快速计算出编辑距离以及编辑操作.
textdistance
textdistance包提供了可用于模糊匹配算法的集合,可以使用如下所示的pip来安装textdistance:
pip install textdistance
但是,如果您希望从算法中获得最快的速度,则可以调整pip install命令,如下所示:
pip install textdistance[extras]
安装完成后,我们可以像下面那样导入textdistance:
import textdistance
All algorithms have some common methods:
.distance(*sequences)— calculate distance between sequences..similarity(*sequences)— calculate similarity for sequences..maximum(*sequences)— maximum possible value for distance and similarity. For any sequence:distance + similarity == maximum..normalized_distance(*sequences)— normalized distance between sequences. The return value is a float between 0 and 1, where 0 means equal, and 1 totally different..normalized_similarity(*sequences)— normalized similarity for sequences. The return value is a float between 0 and 1, where 0 means totally different, and 1 equal.
For example, Hamming distance:
import textdistancetextdistance.hamming('test', 'text') # 1textdistance.hamming.distance('test', 'text') # 1textdistance.hamming.similarity('test', 'text') # 3textdistance.hamming.normalized_distance('test', 'text') # 0.25textdistance.hamming.normalized_similarity('test', 'text') # 0.75textdistance.Hamming(qval=2).distance('test', 'text') # 2
Any other algorithms have same interface.