2021-02-22-隐马尔科夫模型HMM

概念

有些基本的概念， 引用吴军在数学之美[1]之中的描述。

马尔可夫链

随机过程有两个维度的不确定性。马尔可夫为了简化问题，提出了一种简化的假设，即随机过程中各个状态的概率分布，只与它的前一个状态有关, 即

这个假设后来被称为马尔可夫假设，而符合这个假设的随机过程则称为马尔可夫过程，也称为马尔可夫链。

隐含马尔可夫模型

如果马尔科夫链还同时满足以下两个条件：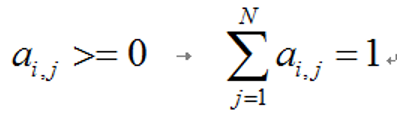

则称该马尔科夫链为马尔可夫模型（Markov Model，HMM）。在马尔科夫模型中，如果状态的转移过程是双重的，且其中状态的转移过程是隐蔽的未知的，则此MM是隐马尔可夫模型（Hidden Markov Model，HMM）：

%3D%5CprodtP(s_t%7Cs%7Bt-1%7D)%5Ccdot%20P(ot%7Cs_t)%0A#card=math&code=P%28s_1%2Cs_2%2Cs_3%2C%5Cdots%2Co_1%2Co_2%2Co_3%2C%5Cdots%29%3D%5Cprod_tP%28s_t%7Cs%7Bt-1%7D%29%5Ccdot%20P%28o_t%7Cs_t%29%0A&id=d25wN)

隐马尔可夫模型可用%0A#card=math&code=%5Clambda%20%3D%20%28A%2C%20B%2C%20%5Cpi%29%0A&id=MDdIA)来描述，

• 初始状态概率分布
• 状态转移概率矩阵
• 观测发射概率矩阵

计算公式：（S 表示状态的有限集合，O 表示观测值的有限集合）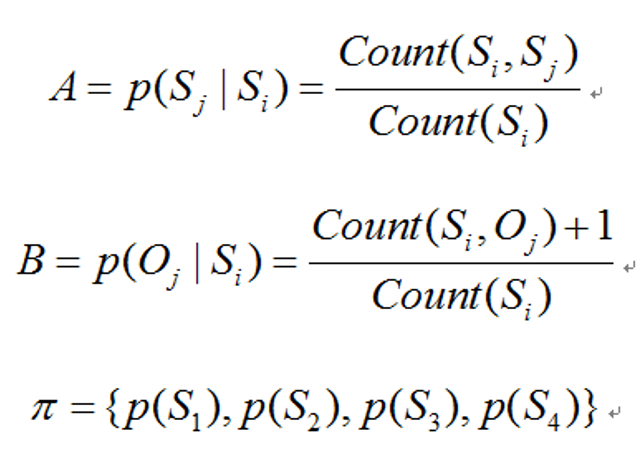

两个基本假设

1. 齐次马尔科夫假设(状态) %20%3D%20P(it%7Ci%7Bt-1%7D)%2C%20t%3D1%2C2%2C%5Cdots%2CT%0A#card=math&code=P%28it%7Ci%7Bt-1%7D%2Co%7Bt-1%7D%2C%5Cdots%2Ci_1%2Co_1%29%20%3D%20P%28i_t%7Ci%7Bt-1%7D%29%2C%20t%3D1%2C2%2C%5Cdots%2CT%0A&id=mSu5N)

假设隐藏的马尔可夫链在任意时刻的状态，只依赖于其前一时刻的状态，与观测无关

1. 观测独立性假设(观测) %3DP(ot%7Ci_t)%0A#card=math&code=P%28o_t%7Ci_T%2Co_T%2Ci%7BT-1%7D%2Co%7BT-1%7D%2C%5Cdots%2Ci%7Bt%2B1%7D%2Co%7Bt%2B1%7D%2Ci_t%2Ci%7Bt-1%7D%2Co_%7Bt-1%7D%2C%5Cdots%2Ci_1%2Co_1%29%3DP%28o_t%7Ci_t%29%0A&id=V45YE)

假设任意时刻的观测，只依赖于该时刻的马尔可夫链的状态 ，与其他观测 及状态无关

三个基本问题

1. 概率计算问题
   输入: 模型#card=math&code=%5Clambda%3D%28A%2CB%2C%5Cpi%29&id=kH4qC), 观测序列#card=math&code=O%3D%28o_1%2Co_2%2C%5Cdots%2Co_T%29&id=za3aT)
   输出: #card=math&code=P%28O%7C%5Clambda%29&id=LXntU)
2. 学习问题
   输入: 观测序列 #card=math&code=O%3D%28o_1%2Co_2%2C%5Cdots%2Co_T%29&id=fXy37)
   输出: 输出#card=math&code=%5Clambda%3D%28A%2CB%2C%5Cpi%29&id=DokI6)
3. 预测问题, 也称为解码问题(Decoding)
   输入: 模型#card=math&code=%5Clambda%3D%28A%2CB%2C%5Cpi%29&id=aa438), 观测序列#card=math&code=O%3D%28o_1%2Co_2%2C%5Cdots%2Co_T%29&id=DJvjU)
   输出: 状态序列 #card=math&code=I%3D%28i_1%2Ci_2%2C%5Cdots%2Ci_T%29&id=jim38)
   因为状态序列是隐藏的，不可观测的，所以叫解码。

图解 HMM 示例

我们以水藻状态与天气状态的关系来说明隐马尔可夫模型，从而预测三天最可能的天气情况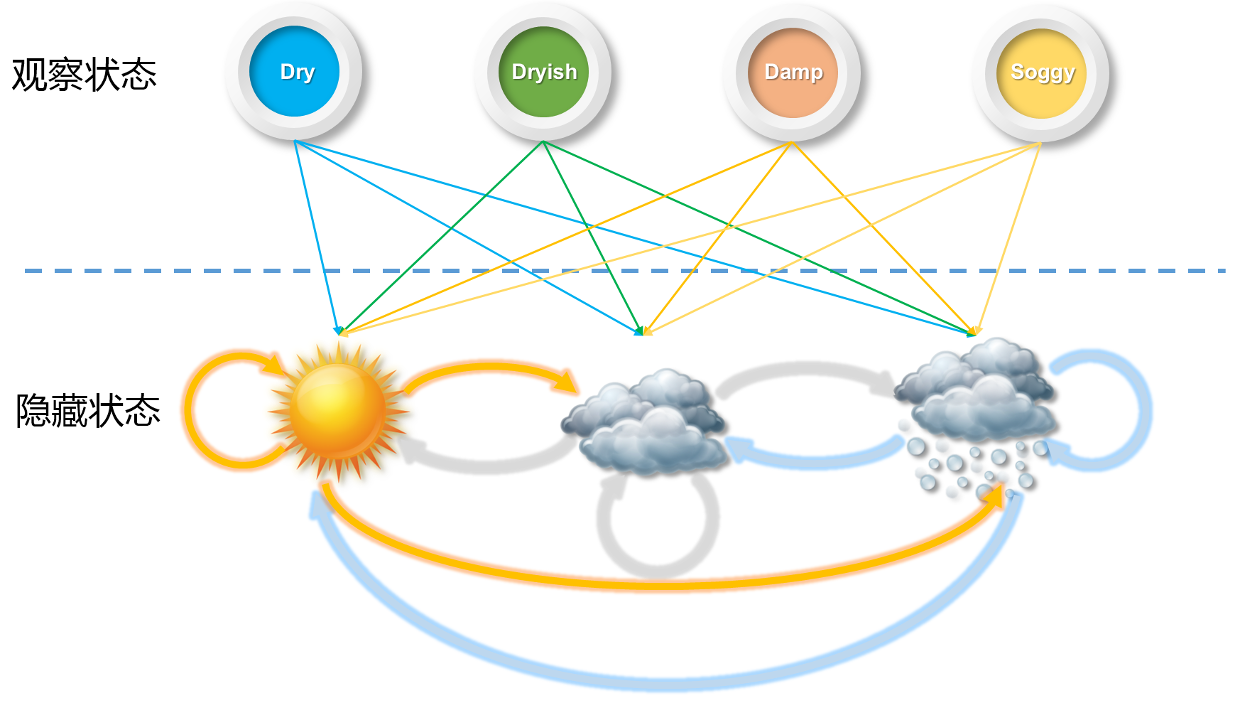

对应隐马尔可夫模型HMM的“五元组”描述：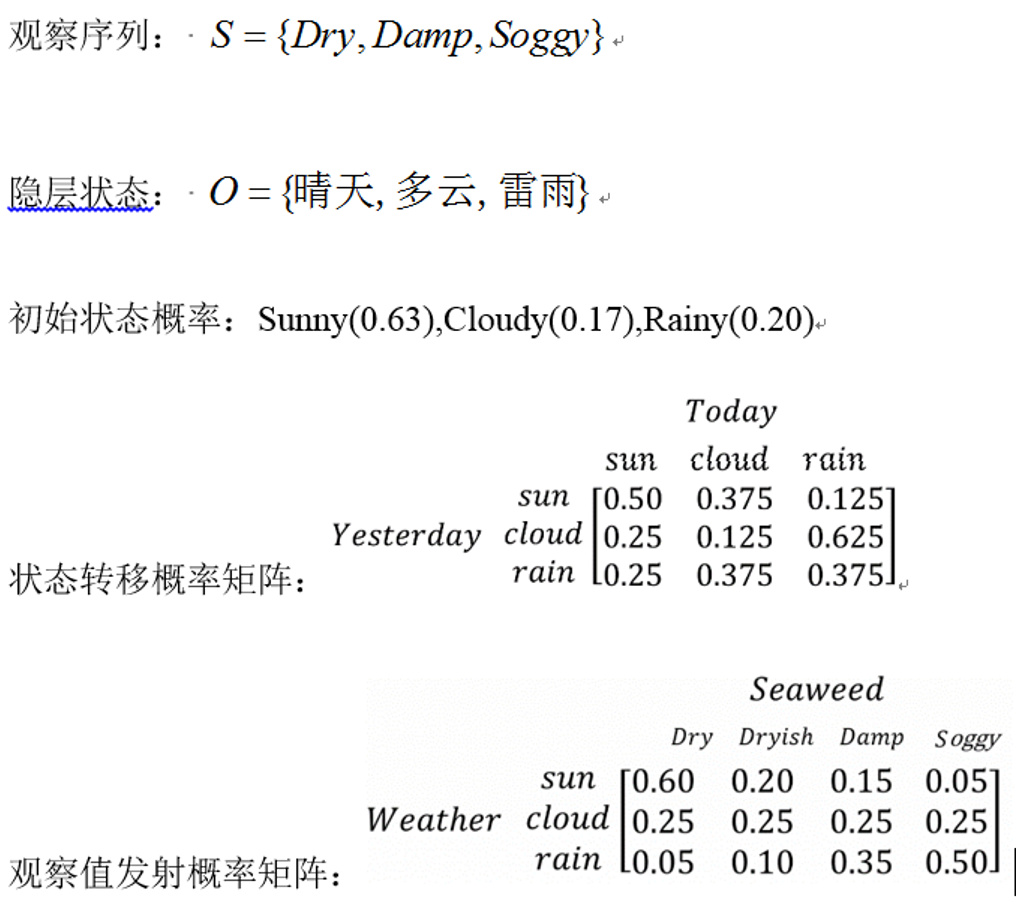

使用viterbi算法解码，求最佳隐含序列：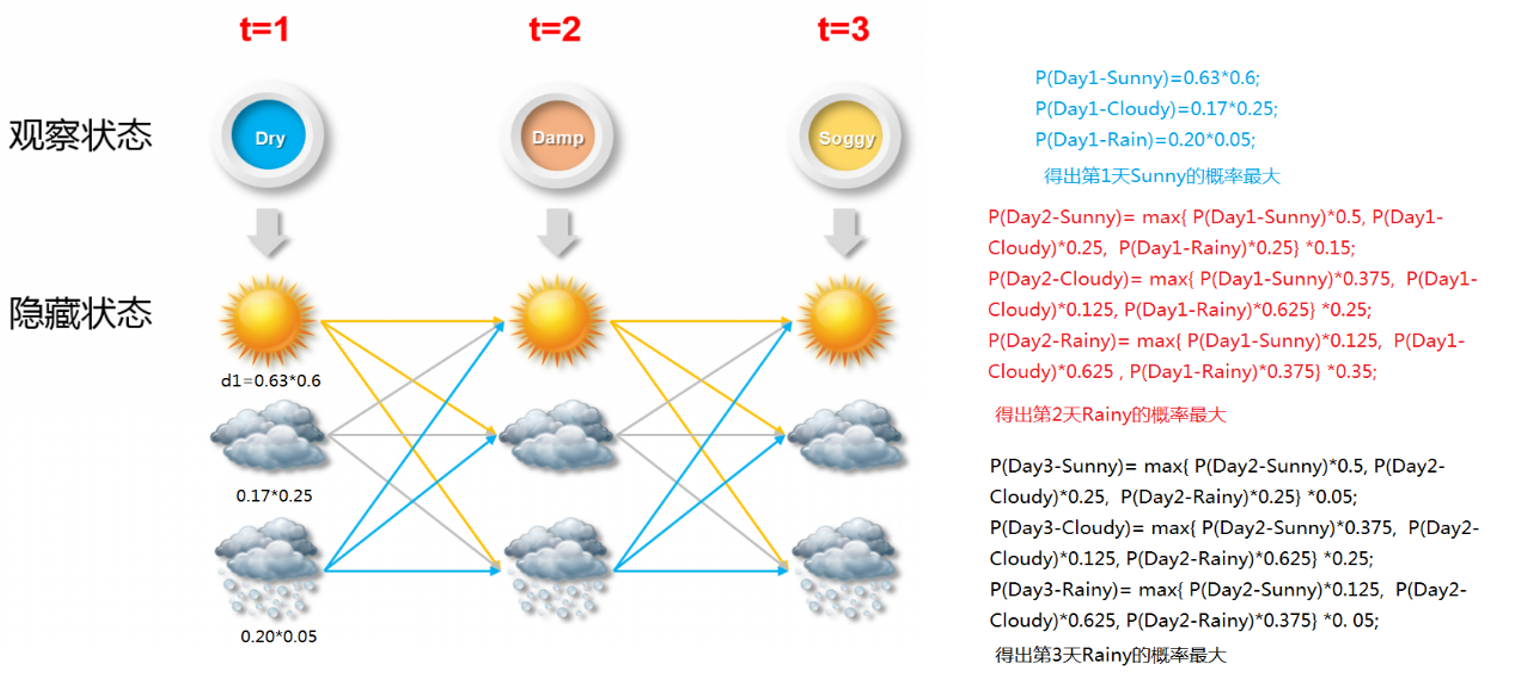

算法

学习算法

前向概率与后向概率

给定马尔可夫模型, 定义到时刻部分观测序列为, 且状态的概率为前向概率, 记作

%3DP(o_1%2Co_2%2C%5Cdots%2Co_t%2Ci_t%3Dq_i%7C%5Clambda)%0A#card=math&code=%5Calpha_t%28i%29%3DP%28o_1%2Co_2%2C%5Cdots%2Co_t%2Ci_t%3Dq_i%7C%5Clambda%29%0A&id=FXh1g)

给定马尔可夫模型, 定义到时刻状态为的条件下, 从到的部分观测序列为的概率为后向概率, 记作

%3DP(o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Cdots%2CoT%7Ci_t%3Dq_i%2C%20%5Clambda)%0A#card=math&code=%5Cbeta_t%28i%29%3DP%28o%7Bt%2B1%7D%2Co_%7Bt%2B2%7D%2C%5Cdots%2Co_T%7Ci_t%3Dq_i%2C%20%5Clambda%29%0A&id=tWvhb)

前向概率从前往后递推， 后向概率从后向前递推。

前向算法

输入:

输出:#card=math&code=P%28O%7C%5Clambda%29&id=kEDCU)

1. 初值 %3D%5Cpi_ib_i(o_1)%2C%20i%3D1%2C2%2C%5Cdots%2CN%0A#card=math&code=%5Calpha_1%28i%29%3D%5Cpi_ib_i%28o_1%29%2C%20i%3D1%2C2%2C%5Cdots%2CN%0A&id=vcVkL)
   观测值, 的含义是对应状态
   这里 是维向量, 和状态集合的大小有关系. 是个联合概率.
2. 递推 %20%3D%20%5Cleft%5B%5Csum%5Climits%7Bj%3D1%7D%5EN%5Calpha_t(j)a%7Bji%7D%5Cright%5Dbi(o%7Bt%2B1%7D)%5Ccolor%7Bblack%7D%2C%20%5C%20%20%20i%3D1%2C2%2C%5Cdots%2CN%2C%20%5C%20t%20%3D%201%2C2%2C%5Cdots%2CT-1%0A#card=math&code=%5Ccolor%7Bred%7D%5Calpha%7Bt%2B1%7D%28i%29%20%3D%20%5Cleft%5B%5Csum%5Climits%7Bj%3D1%7D%5EN%5Calphat%28j%29a%7Bji%7D%5Cright%5Dbi%28o%7Bt%2B1%7D%29%5Ccolor%7Bblack%7D%2C%20%5C%20%20%20i%3D1%2C2%2C%5Cdots%2CN%2C%20%5C%20t%20%3D%201%2C2%2C%5Cdots%2CT-1%0A&id=Xy25d)
   转移矩阵维度, 观测矩阵维度, 具体的观测值可以表示成one-hot形式, 维度, 所以的维度是
3. 终止 %3D%5Csum%5Climits%7Bi%3D1%7D%5EN%5Calpha_T(i)%3D%5Ccolor%7Bred%7D%5Csum%5Climits%7Bi%3D1%7D%5EN%5CalphaT(i)%5Cbeta_T(i)%0A#card=math&code=P%28O%7C%5Clambda%29%3D%5Csum%5Climits%7Bi%3D1%7D%5EN%5CalphaT%28i%29%3D%5Ccolor%7Bred%7D%5Csum%5Climits%7Bi%3D1%7D%5EN%5Calpha_T%28i%29%5Cbeta_T%28i%29%0A&id=a94xc)
   注意, 这里#card=math&code=O%5Crightarrow%20%28o_1%2C%20o_2%2C%20o_3%2C%5Cdots%2C%20o_t%29&id=hOCDS), 见前面前向概率的定义#card=math&code=P%28o_1%2Co_2%2C%5Cdots%2Co_t%2Ci_t%3Dq_i%7C%5Clambda%29&id=Dxn8U), 所以, 对求和能把联合概率中的消掉.
   这个书里面解释的部分有说.

前向算法计算#card=math&code=P%28O%7C%5Clambda%29&id=CfZ2G)的复杂度是#card=math&code=O%28N%5E2T%29&id=pylkI)阶的，直接计算的复杂度是#card=math&code=O%28TN%5ET%29&id=z608x)阶，所以时候并没什么改善。

红色部分为后补充了#card=math&code=%5Cbeta_T%28i%29&id=SxVCF)项，这项为1,此处注意和后面的后向概率对比。

后向算法

输入:
输出:#card=math&code=P%28O%7C%5Clambda%29&id=Fx7hW)

1. 终值

%3D1%2C%20i%3D1%2C2%2C%5Cdots%2CN%0A#card=math&code=%5Cbeta_T%28i%29%3D1%2C%20i%3D1%2C2%2C%5Cdots%2CN%0A&id=sF2pN)

在时刻, 观测序列已经确定.

1. 递推

%3D%5Csum%5Climits%7Bj%3D1%7D%5ENa%7Bij%7Dbj(o%7Bt%2B1%7D)%5Cbeta%7Bt%2B1%7D(j)%5Ccolor%7Bblack%7D%2C%20i%3D1%2C2%2C%5Cdots%2CN%2C%20t%3DT-1%2C%20T-2%2C%5Cdots%2C1%0A#card=math&code=%5Ccolor%7Bred%7D%5Cbeta_t%28i%29%3D%5Csum%5Climits%7Bj%3D1%7D%5ENa%7Bij%7Db_j%28o%7Bt%2B1%7D%29%5Cbeta_%7Bt%2B1%7D%28j%29%5Ccolor%7Bblack%7D%2C%20i%3D1%2C2%2C%5Cdots%2CN%2C%20t%3DT-1%2C%20T-2%2C%5Cdots%2C1%0A&id=LIy3Z)

从后往前推

1. 
   

%3D%5Csum%5Climits%7Bi%3D1%7D%5EN%5Cpi_ib_i(o_1)%5Cbeta_1(i)%3D%5Ccolor%7Bred%7D%5Csum%5Climits%7Bi%3D1%7D%5Calpha1(i)%5Cbeta_1(i)%0A#card=math&code=P%28O%7C%5Clambda%29%3D%5Csum%5Climits%7Bi%3D1%7D%5EN%5Cpiib_i%28o_1%29%5Cbeta_1%28i%29%3D%5Ccolor%7Bred%7D%5Csum%5Climits%7Bi%3D1%7D%5Calpha_1%28i%29%5Cbeta_1%28i%29%0A&id=PG2fr)

• 这里需要注意下，按照后向算法，在递推过程中会越来越小，如果层数较多，怕是#card=math&code=P%28O%7C%5Clambda%29&id=BJQDw)会消失
• 另外一个要注意的点
• 注意，红色部分为后补充，结合前面的前向概率最后的红色部分一起理解。

小结

求解的都是观测序列概率
观测序列概率#card=math&code=P%28O%7C%5Clambda%29&id=qr2SI)统一写成

%3D%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Calphat(i)a%7Bij%7Dbj(o%7Bt%2B1%7D%5Cbeta%7Bt%2B1%7D(j))%2C%5C%20t%3D1%2C2%2C%5Cdots%2CT-1%0A#card=math&code=P%28O%7C%5Clambda%29%3D%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Calpha_t%28i%29a%7Bij%7Dbj%28o%7Bt%2B1%7D%5Cbeta_%7Bt%2B1%7D%28j%29%29%2C%5C%20t%3D1%2C2%2C%5Cdots%2CT-1%0A&id=vtGmB)

%20%3D%20%5Calpha%20ABo%5Cbeta#card=math&code=P%28O%7C%5Clambda%29%20%3D%20%5Calpha%20ABo%5Cbeta&id=Sng3U)

其实前向和后向不是为了求整个序列的概率，是为了求中间的某个点，前向后向主要是有这个关系:

%5Cbeta_t(i)%3DP(i_t%3Dq_i%2CO%7C%5Clambda)%0A#card=math&code=%5Calpha_t%28i%29%5Cbeta_t%28i%29%3DP%28i_t%3Dq_i%2CO%7C%5Clambda%29%0A&id=XXbfy)

当或者的时候，单独用后向和前向就可以求得#card=math&code=P%28O%7C%5Clambda%29&id=sjajw)，分别利用前向和后向算法均可以求解#card=math&code=P%28O%7C%5Clambda%29&id=G2vuv)，结果一致。

利用上述关系可以得到下面一些概率和期望，这些概率和期望的表达式在后面估计模型参数的时候有应用。

预测算法

近似算法(MAP)

每个时刻最有可能的状态是

%5Cright%5D%2C%20t%3D1%2C2%2C%5Cdots%2CT%0A#card=math&code=it%5E%2A%3D%5Carg%20%5Cmax%5Climits%7B1%5Cleqslant%20i%5Cleqslant%20N%7D%5Cleft%5B%5Cgamma_t%28i%29%5Cright%5D%2C%20t%3D1%2C2%2C%5Cdots%2CT%0A&id=ZranM)

得到序列#card=math&code=I%5E%2A%3D%28i_1%5E%2A%2Ci_2%5E%2A%2C%5Cdots%2Ci_T%5E%2A%29&id=wm5mw)

这个算法, 在输出每个状态的时候, 只考虑了当前的状态.

维特比算法(Viterbi)

Viterbi算法是一种动态规划算法，用来寻找由观测信息产生的最可能隐状态序列 (Viterbi路径)

• 计算过程：计算在前一个状态出现的条件下，当前状态出现的概率，取最大的那个概率作为当前状态出现的概率。最后通过回溯得到最佳的隐含状态序列