2021-09-06-聚类算法

layout: post # 使用的布局（不需要改）
title: 文本聚类 # 标题
subtitle: 正确使用kmeans聚类的姿势
date: 2019-09-06 # 时间
author: NSX # 作者
header-img: img/post-bg-2015.jpg #这篇文章标题背景图片
catalog: true # 是否归档
tags: #标签
- 文本聚类

1. 聚类介绍

• 聚类试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个“簇”(cluster).
• 通过这样的划分，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。
• 聚类过程仅能自动形成簇结构，簇所对应的概念语义需由使用者自己来把握。
• 聚类既能作为一个单独的过程用于寻找数据内在的分布结构，也可以作为分类等其他学习任务的前驱过程。

1.1 聚类算法：

• 基于原型的聚类(Prototype-based Clustering)
  • K均值聚类(K-means)
  • 学习向量量化聚类(Learning Vector Quantization)
  • 高斯混合模型聚类 (Gaussian Mixture Model)
• 基于密度的聚类 (Density-based Clustering)
  • DBSCAN (Density-Based Spatial Clustering of Application with Noise)
  • OPTICS (Ordering Points To Identify the Clustering Structure)
• 层次聚类 (Hierarchical Clustering)
• 基于模型的聚类 (Model-based Clustering)
  • 混合回归模型 (Mixture Regression Model)

    1.2 聚类的一般过程

1. 数据准备：特征标准化和降维
2. 特征选择：从最初的特征中选择最有效的特征，并将其存储在向量中
3. 特征提取：通过对选择的特征进行转换形成新的突出特征
4. 聚类：基于某种距离函数进行相似度度量，获取簇
5. 聚类结果评估：分析聚类结果，如距离误差和(SSE)等

1.3 聚类距离计算：

距离度量(distance measure)函数 #card=math&code=d%28%29&id=EX1EA) 需满足的基本性质：

• 非负性： %3E%3D0#card=math&code=d%28x%2Cy%29%3E%3D0&id=d93Gt)
• 同一性：%20%3D%200%20%5Cquad%20if%20%5Cquad%20and%20%5Cquad%20only%20%5Cquad%20if%20%5Cquad%20x%3Dy#card=math&code=d%28x%2Cy%29%20%3D%200%20%5Cquad%20if%20%5Cquad%20and%20%5Cquad%20only%20%5Cquad%20if%20%5Cquad%20x%3Dy&id=qpbV0)
• 对称性： %20%3D%20d(y%2Cx)#card=math&code=d%28x%2Cy%29%20%3D%20d%28y%2Cx%29&id=Vu7Bm)
• 直递性：%20%5Cleq%20d(x%2Cz)%20%2B%20d(z%2Cy)#card=math&code=d%28x%2Cy%29%20%5Cleq%20d%28x%2Cz%29%20%2B%20d%28z%2Cy%29&id=ZrPAU) (可不满足)

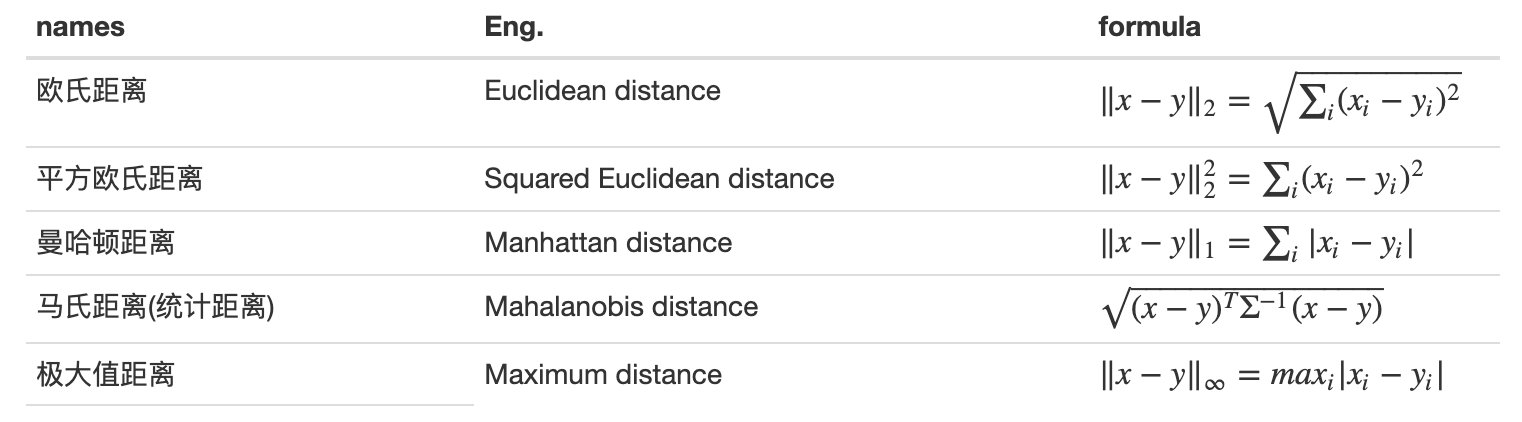
常用基于距离的相似度度量方法：

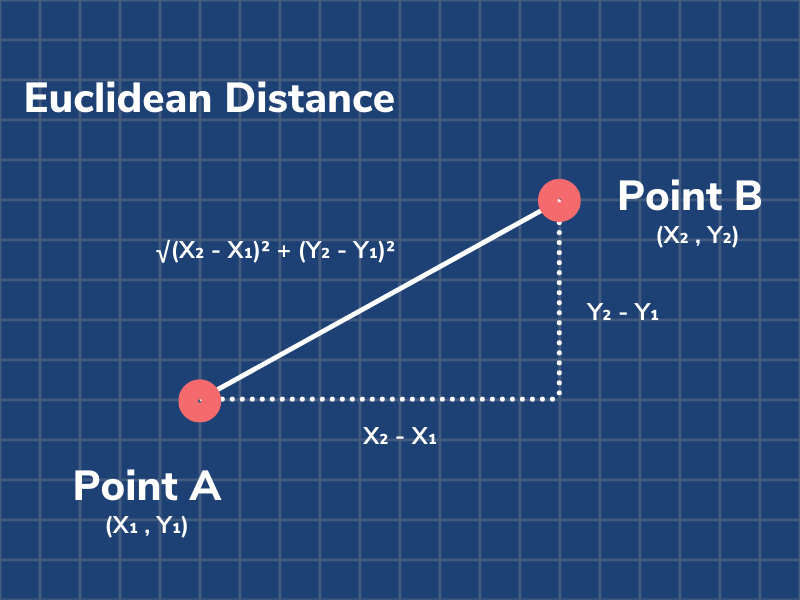
欧几里得距离：

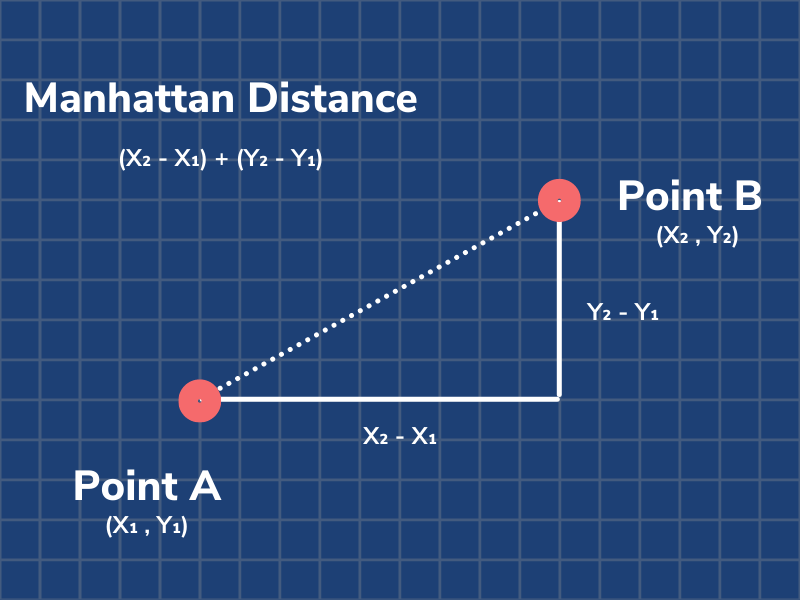
曼哈顿距离：

1.4 聚类性能度量：

聚类性能度量亦称聚类“有效性指标”(validity index).

设置聚类性能度量的目的:

• 对聚类结果，通过某种性能度量来评估其好坏；
• 若明确了最终将要使用的性能度量，则可直接将其作为聚类过程的优化目标，从而更好地得到符合要求的聚类结果。

什么样的聚类结果比较好？

• “簇内相似度”(intra-cluster similarity)高
• “蔟间相似度”(inter-cluster similarity)低

聚类性能度量分类：

• “外部指标”(external index) ：将聚类结果与某个“参考模型”(reference model)进行比较
• “内部指标”(internal index): 直接考察聚类结果而不利用任何参考模型

性能度量指标：

(1) 外部指标

(2) 内部指标

2 聚类算法介绍及实现

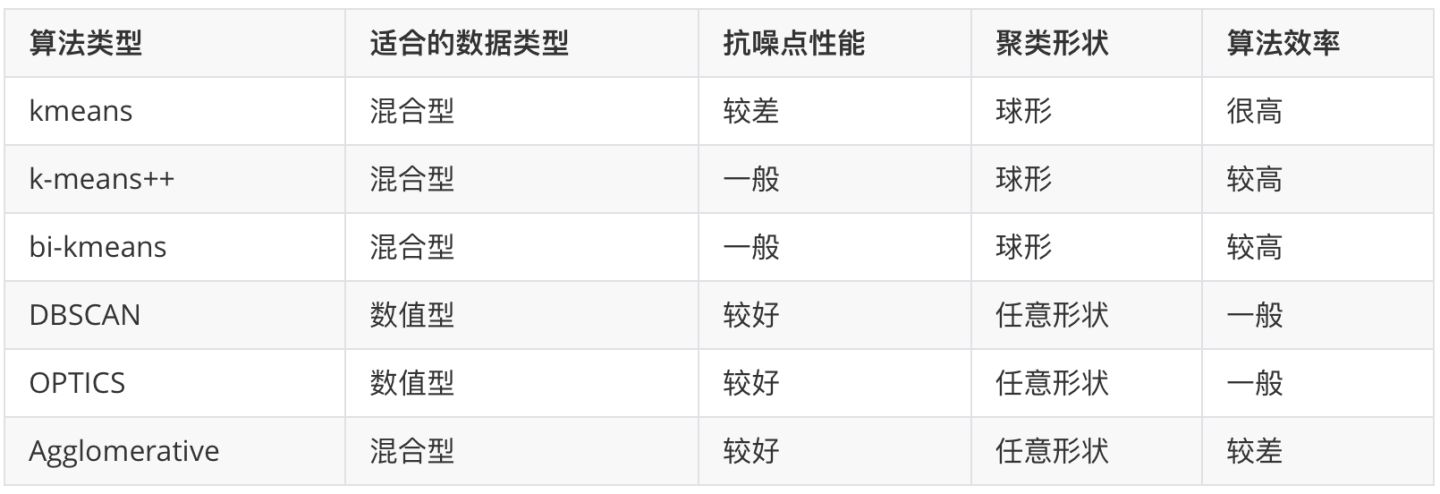
聚类算法类型：

• 基于原型的聚类(Prototype-based Clustering)
  • K均值聚类(K-means )
  • 学习向量量化聚类(Learning vector Quantization)
  • 高斯混合聚类(Mixture-of-Gaussian)
• 基于密度的聚类(Density-based Clustering)
• 层次聚类(Hierarchical Clustering)

2.1 基于原型的聚类

原型聚类prototype-based clustering，假设聚类结构能通过一组原型刻画（原型，即簇类的数目或者聚类中心）. 通常情况下, 算法先对原型进行初始化, 然后对原型进行迭代更新求解, 采用不同的原型表示, 不同的求解方式,将产生不同的算法.

2.1.1 K-means

(1) 算法介绍

给定样本集 , K-means 算法针对聚类所得簇划分 , 最小化平方误差:

其中 是簇 的均值向量：

直观上看, 平方误差在一定程度上刻画了簇内样本围绕均值向量的紧密程度, 值越小簇内样本相似度越高。但最小化 不容易，是一个NP难问题, K-means 算法采用了贪心策略，通过迭代优化来近似求解 EE 的最小值。具体算法如下：

(2) 算法实现

我们的 k-means 实现将分为五个辅助方法和一个运行算法的主循环：

1.计算成对距离

def pairwise_dist(self, x, y):
        """
        Args:
            x: N x D numpy array
            y: M x D numpy array
        Return:
            dist: N x M array, where dist2[i, j] is the euclidean distance between 
            x[i, :] and y[j, :]
        """
        xSumSquare = np.sum(np.square(x),axis=1);
        ySumSquare = np.sum(np.square(y),axis=1);
        mul = np.dot(x, y.T);
        dists = np.sqrt(abs(xSumSquare[:, np.newaxis] + ySumSquare-2*mul))
        return dists

pairwise_dist 函数与前面描述的相似性函数等效。这是我们比较两点相似性的指标。在这里，我使用的是欧几里得距离。我使用的公式可能看起来与欧几里德距离函数的常规公式不同。这是因为我们正在执行矩阵操作，而不是使用两个单个向量。在这里深入阅读。

2.初始化中心

def _init_centers(self, points, K, **kwargs):
        """
        Args:
            points: NxD numpy array, where N is # points and D is the dimensionality
            K: number of clusters
            kwargs: any additional arguments you want
        Return:
            centers: K x D numpy array, the centers. 
        """
        row, col = points.shape
        retArr = np.empty([K, col])
        for number in range(K):
            randIndex = np.random.randint(row)
            retArr[number] = points[randIndex]
        return retArr

该函数接收点数组并随机选择其中的 K 个作为初始质心。该函数仅返回 K 个选定点。

3.更新分配

def _update_assignment(self, centers, points):
        """
        Args:
            centers: KxD numpy array, where K is the number of clusters, and D is the dimension
            points: NxD numpy array, the observations
        Return:
            cluster_idx: numpy array of length N, the cluster assignment for each point
        Hint: You could call pairwise_dist() function.
        """
        row, col = points.shape
        cluster_idx = np.empty([row])
        distances = self.pairwise_dist(points, centers)
        cluster_idx = np.argmin(distances, axis=1)
        return cluster_idx

更新分配函数负责选择每个点应该属于哪个集群。首先，我使用 pairwise_dist 函数计算每个点和每个质心之间的距离。然后，我得到每一行的最小距离的索引。最小距离的索引也是给定数据点的聚类分配索引，因为我们希望将每个点分配给最近的质心。

4.更新中心

def _update_centers(self, old_centers, cluster_idx, points):
        """
        Args:
            old_centers: old centers KxD numpy array, where K is the number of clusters, and D is the dimension
            cluster_idx: numpy array of length N, the cluster assignment for each point
            points: NxD numpy array, the observations
        Return:
            centers: new centers, K x D numpy array, where K is the number of clusters, and D is the dimension.
        """
        K, D = old_centers.shape
        new_centers = np.empty(old_centers.shape)
        for i in range(K):
            new_centers[i] = np.mean(points[cluster_idx == i], axis = 0)
        return new_centers

更新中心功能负责对属于给定集群的所有点进行平均。该平均值是相应聚类的新质心。该函数返回新中心的数组。

5.计算损失

def _get_loss(self, centers, cluster_idx, points):
        """
        Args:
            centers: KxD numpy array, where K is the number of clusters, and D is the dimension
            cluster_idx: numpy array of length N, the cluster assignment for each point
            points: NxD numpy array, the observations
        Return:
            loss: a single float number, which is the objective function of KMeans. 
        """
        dists = self.pairwise_dist(points, centers)
        loss = 0.0
        N, D = points.shape
        for i in range(N):
            loss = loss + np.square(dists[i][cluster_idx[i]])
        return loss

损失函数是我们评估聚类算法性能的指标。我们的损失只是每个点与其聚类质心之间的平方距离之和。在我们的实现中，我们首先调用成对距离来获得每个点和每个中心之间的距离矩阵。我们使用 cluster_idx 为每个点选择与集群对应的适当距离2。

主循环

def __call__(self, points, K, max_iters=100, abs_tol=1e-16, rel_tol=1e-16, verbose=False, **kwargs):
        """
        Args:
            points: NxD numpy array, where N is # points and D is the dimensionality
            K: number of clusters
            max_iters: maximum number of iterations (Hint: You could change it when debugging)
            abs_tol: convergence criteria w.r.t absolute change of loss
            rel_tol: convergence criteria w.r.t relative change of loss
            verbose: boolean to set whether method should print loss (Hint: helpful for debugging)
            kwargs: any additional arguments you want
        Return:
            cluster assignments: Nx1 int numpy array
            cluster centers: K x D numpy array, the centers
            loss: final loss value of the objective function of KMeans
        """
        centers = self._init_centers(points, K, **kwargs)
        for it in range(max_iters):
            cluster_idx = self._update_assignment(centers, points)
            centers = self._update_centers(centers, cluster_idx, points)
            loss = self._get_loss(centers, cluster_idx, points)
            K = centers.shape[0]
            if it:
                diff = np.abs(prev_loss - loss)
                if diff < abs_tol and diff / prev_loss < rel_tol:
                    break
            prev_loss = loss
            if verbose:
                print('iter %d, loss: %.4f' % (it, loss))
        return cluster_idx, centers, loss

现在，在主循环中，我们可以组合所有实用函数并实现伪代码。首先，中心用_init_centers随机初始化。然后，对于指定的迭代次数，我们重复update_assignment和update_centers步骤。每次迭代后，我们计算总损失并将其与之前的损失进行比较。如果差异小于我们的阈值，则算法执行完成。

补充：

k-means 优点：

• 计算复杂度低，为 ，其中 为迭代次数。
  通常 和 要远远小于 ，此时复杂度相当于 。
• 思想简单，容易实现。

k-means 缺点：

• 需要首先确定聚类的数量
• 分类结果严重依赖于分类中心的初始化。
  通常进行多次k-means，然后选择最优的那次作为最终聚类结果。
• 结果不一定是全局最优的，只能保证局部最优。
• 对噪声敏感。因为簇的中心是取平均，因此聚类簇很远地方的噪音会导致簇的中心点偏移。
• 无法解决不规则形状的聚类。
• 无法处理离散特征，如：国籍、性别 等。

正确使用「K均值聚类」的Tips

1. 输入数据一般需要做缩放，如标准化。原因很简单，K均值是建立在距离度量上的，因此不同变量间如果维度差别过大，可能会造成少数变量“施加了过高的影响而造成垄断”。
2. 输出结果非固定，多次运行结果可能不同。首先要意识到K-means中是有随机性的，从初始化到收敛结果往往不同。一种看法是强行固定随机性，比如设定sklearn中的random state为固定值。另一种看法是，如果你的K均值结果总在大幅度变化，比如不同簇中的数据量在多次运行中变化很大，那么K均值不适合你的数据，不要试图稳定结果 [2]。
3. 运行时间往往可以得到优化，选择最优的工具库。基本上现在的K均值实现都是K-means++，速度都不错。但当数据量过大时，依然可以使用其他方法，如MiniBatchKMeans [3]。上百万个数据点往往可以在数秒钟内完成聚类，推荐Sklearn的实现。
4. 高维数据上的有效性有限。建立在距离度量上的算法一般都有类似的问题，那就是在高维空间中距离的意义有了变化，且并非所有维度都有意义。这种情况下，K均值的结果往往不好，而通过划分子空间的算法（sub-spacing method）效果可能更好。
5. 运行效率与性能之间的取舍。

K值怎么确定

• 使用 K 均值算法，性能可能会因您使用的集群数量而有很大差异。要知道，K设置得越大，样本划分得就越细，每个簇的聚合程度就越高，误差平方和SSE自然就越小。所以不能单纯像选择初始点那样，用不同的K来做尝试，选择SSE最小的聚类结果对应的K值，因为这样选出来的肯定是你尝试的那些K值中最大的那个。
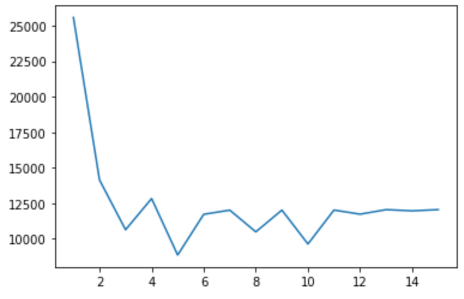
• “手肘法”（Elbow Method）
  为了使用肘部方法，您只需多次运行 K-means 算法，每次迭代将聚类数增加一个。记录每次迭代的损失，然后制作 num cluster vs loss 的折线图。

下面是肘部方法的简单实现：

运行此方法将输出一个类似于您在下面看到的图：

现在，为了选择正确数量的簇，我们进行目视检查。损耗曲线开始弯曲的点称为 肘点。肘点代表误差和聚类数量之间的合理权衡。在此示例中，肘点位于x = 3 处。这意味着最佳聚类数为 3。

def find_optimal_num_clusters(self, data, max_K=15):
        """
        Plots loss values for different number of clusters in K-Means
        Args:
            image: input image of shape(H, W, 3)
            max_K: number of clusters
        Return:
            None (plot loss values against number of clusters)
        """
        y_val = np.empty(max_K)
        for i in range(max_K):
            cluster_idx, centers, y_val[i] = KMeans()(data, i + 1)
        plt.plot(np.arange(max_K) + 1, y_val)
        plt.show()
        return y_val

from sklearn.cluster 
import KMeans
loss = []
for i in range(1, 10):    
  kmeans = KMeans(n_clusters=i, max_iter=100).fit(p_list)    
  loss.append(kmeans.inertia_ / point_number / K)    
plt.plot(range(1, 10), loss)plt.show()

2.1.2 k-means++

k-means++是针对k-means中初始质心点选取的优化算法。该算法的流程和k-means类似，改变的地方只有初始质心的选取，该部分的算法流程如下

算法步骤：

• 从 中随机选择1个样本作为初始均值向量组 。
• 迭代，直到初始均值向量组有 个向量。
  假设初始均值向量组为 。迭代过程如下：
  • 对每个样本 ，分别计算其距 的距离。这些距离的最小值记做 。
  • 对样本 ，其设置为初始均值向量的概率正比于 。即：离所有的初始均值向量越远，则越可能被选中为下一个初始均值向量。
  • 以概率分布 （未归一化的）随机挑选一个样本作为下一个初始均值向量 。
• 一旦挑选出初始均值向量组 ，剩下的迭代步骤与k-means 相同。

2.1.3 LVQ

(1) 算法介绍

Learning vector Quantization (LVQ) 假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。使用通过LVQ得到的原型向量来代表整个簇的过程，称为“向量量化”（Vector Quantization），这种数据压缩方法属于“有损压缩”（Lossy Compression）。

LVQ的目标是学得一组原型向量 ，每个原型向量代表一个聚类簇。LVQ在训练过程中通过对神经元权向量（原型向量）的不断更新，对其学习率的不断调整，能够使不同类别权向量之间的边界逐步收敛至贝叶斯分类边界。算法中，对获胜神经元（最近邻权向量）的选取是通过计算输入样本和权向量之间的距离的大小来判断的。

具体算法流程图如下所示：

算法解释

• 算法第1行：对原型向量进行初始化。例如：对第#card=math&code=i%2C%20i%3D%281%2C2%2C%E2%80%A6%2Cq%29&id=qL4lO) 个簇,从类别标记为 的样本中随机选取一个作为原型向量。如果类别数小于聚类数，即 k>m ，则重新从第一个类别中继续选取；
• 算法第2-12行：对原型向量进行迭代优化，直到算法收敛。在每一轮迭代中，算法随机选取一个有标记训练样本，找出与其距离最近的原型向量，并根据两者的类别标记是否一致来对原型向量进行相应的更新。
• 算法第2-5行：从样本集中随机选取一个样本 ，计算该样本与每个原型向量 之间的欧式距离，并找到与该样本距离最近的原型向量 的类别标记
• 第6-10行：如何更新原型向量。迭代过程如下：
  • 从样本集 中随机选取样本 ，挑选出距离 最近的原型向量 ： 。
  • 如果 的类别等于 ，则： ，将该原型向量更靠近
  • 如果 的类别不等于 ，则： ，将该原型向量更远离

在原型向量的更新过程中：

• 如果 的类别等于 ，则更新后， 与 距离为：
  

  即，更新后的原型向量 距离 更近。

• 如果 的类别不等于 ，则更新后， 与 距离为：
  
  即，更新后的原型向量 距离 更远。

  • 算法第12行：若算法的停止条件已满足(例如已达到最大迭代轮数，或原型向量更新很小甚至不再更新)，则将当前原型向量作为最终结果返回。
  • 在学得一组原型向量 后即可实现对样本空间 的簇划分. 对任意样本 , 他将被划入与其距离最近的原型向量所代表的簇中

可能涉及到的问题：

首先，既然已经有标签数据，那么为什么还要进行聚类呢？

我们输入的先验标签数据不一定是绝对真实的取值，可能是其他分类器输出的结果，可能是片面的、残缺的，需要靠聚类进行矫正和修补。（可以将先验知识当做一个约束值，该算法相当于在已知的约束条件下求解最最优值的过程）

对于矫正作用，由于输入的只有标签值，需要靠聚类进行类别边界的拟合；对于修补作用，由于LVQ聚类算法允许聚类的簇比输入的标签的类别多，这意味着一个类别可以被重新分割成多个类别。

其次，标签值是必须的吗？

一种说法是标签值是非必须的，如果没有先验的标签值，可以输入随机的标签值。我不太认同这种做法。因为标签值是一种约束，随机的约束即相当于没有约束，那么LVQ算法其实就退化为一般的聚类的算法，甚至更加严重，随机会使得系统更加混沌，算法会因为错误的指导给出效果更差的答案。所以我更偏向于将其归为半监督的聚类算法。

其他注意事项

• 样本异常点对聚类有影响，一般我们需要提前剔除掉
• 难以应用在高维特征空间
• 可以多选择几个簇心，来降低压缩率，提高保持较高的精度？
• 为了得到更精确的代表点需要调整迭代次数和学习率，时间复杂度比较

(2) LVQ算法实现

《手写LVQ（学习向量量化）聚类算法》 《ml/lvq/lvq_test/lvq_test.py》√ 《neupy/neupy/algorithms/competitive/lvq.py 》√ 《Learning Vector Quantization详解》

def lvq(data: np, k_num: int, labels: list, lr=0.01, max_iter=15000, delta=1e-3):
    """
    :param data: 样本集, 最后一列feature表示原始数据的label
    :param k_num: 簇数，原型向量个数
    :param labels: 1-dimension list or array,label of the data（去重）
    :param max_iter: 最大迭代数
    :param lr: 学习效率
    :param delta: max distance for two vectors to be 'equal'.
    :return: 返回向量中心点、簇标记
    """
    # 随机初始化K个原型向量
    v = rand_initial_center(data, k_num, labels)
    # 确认是否所有中心向量均已更新
    all_vectors_updated = np.zeros(shape=(k_num,), dtype=np.bool)
    # 记录各个中心向量的更新次数
    v_update_cnt = np.zeros(k_num, dtype=np.float32)
    j = 0
    while True:
        j = j + 1
        if j%100==0:
            print("iter:", j)
        # 迭代停止条件：已到达最大迭代次数，或者原型向量全都更新过
        if j >= max_iter or all_vectors_updated.all():
            break
        # # 迭代停止条件：超过阈值且每个中心向量都更新超过5次则退出
        # if j >= max_iter and sum(v_update_cnt > 5) == k_num:
        #     break
        # 随机选择一个样本, 并计算与当前各个簇中心点的距离, 取距离最小的
        sel_sample = random.choice(data)
        min_dist = distance(sel_sample, v[0])
        sel_k = 0
        for ii in range(1, k_num):
            dist = distance(sel_sample, v[ii])
            if min_dist > dist:
                min_dist = dist
                sel_k = ii
        # 保存更新前向量
        temp_v = v[sel_k].copy()
        # 更新v：如果标签相同，则q更新后接近样本x，否则远离
        if sel_sample[-1] == v[sel_k][-1]:
            v[sel_k][0:-1] = v[sel_k][0:-1] + lr * (sel_sample[0:-1] - v[sel_k][0:-1])
        else:
            v[sel_k][0:-1] = v[sel_k][0:-1] - lr * (sel_sample[0:-1] - v[sel_k][0:-1])
        # 更新记录数组（更新后簇心基本不变，就认为更新好了）
        if distance(temp_v, v[sel_k]) < delta:
            all_vectors_updated[sel_k] = True
        # v的更新次数+1
        v_update_cnt[sel_k] = v_update_cnt[sel_k] + 1
    # 更新完毕后, 把各个样本点进行标记, 记录放在categories变量里
    m, n = np.shape(data)
    cluster_assment = np.mat(np.zeros((m, 2)), dtype=np.float32)
    for i in range(m):
        min_distji = np.inf
        min_distji_index = -1
        for j in range(k_num):
            distji = distance(data[i, :], v[j, :])
            # print(distji)
            if min_distji > distji:
                min_distji = distji
                min_distji_index = j
        cluster_assment[i, 0] = min_distji_index
        cluster_assment[i, 1] = min_distji
    return v, cluster_assment

(3) LVQ2算法改进

LVQ算法中，对于某个输入向量X，算法只对与其具有最小Euclidean距离的权向量 进行调整。

在LVQ2[2]中，算法还要考虑与X具有次近Euclidean距离的权向量，X与及间的距离分别记为 与 。如果下述3个条件都满足的话，算法就对及同时进行调整，否则就按照原先的LVQ算法调整权向量：

1. 及代表不同的分类。
2. 次近权向量与X代表同一个分类。
3. 与 大致相等。一般来说．如果 与 能够满足#card=math&code=d_k%2Fd_r%3E%281%E4%B8%80%EF%BF%A1%29&id=lT1sr)且 #card=math&code=d_r%2Fd_k%3C%281%2B%EF%BF%A1%29&id=SdGdq)，我们就认为 与 是大致相等的，其中￡的取值依赖于训练例的多少。

在上述3个条件都满足的情况下，按下述公式调整及，使得远离输入向量X，而向输入向量的方向靠近：

1. %3DW_k(old)%E4%B8%80%5Calpha(X%E2%80%94W_k(old))#card=math&code=W_k%28new%29%3DW_k%28old%29%E4%B8%80%5Calpha%28X%E2%80%94W_k%28old%29%29&id=XvDsJ)
2. %3DW_r(old)%2B%5Calpha(X%E2%80%94W_r(old))#card=math&code=W_r%28new%29%3DW_r%28old%29%2B%5Calpha%28X%E2%80%94W_r%28old%29%29&id=eFhYu)

LVQ2算法通过同时考察两个权值向量及，可以加快算法的收敛速度，使得各个权向量快速的向目标位置移动。

(4) LVQ2.1算法改进

LVQ2.1在LVQ2的基础上做了一些改进．LVQ2.1也是同时考察与某个输入向量X最近的两个权向量 ，但并不关心哪一个离X更近(对应的距离分别为)。当下面两个条件同时满足时将对进行调整：

1. 中，有一个权向量代表的分类和X所表示的一致，而另一个不一致。
2. #card=math&code=max%5Bd%7Bc_1%7D%EF%BC%8Fd%7Bc2%7D%2Cd%7Bc2%7D%EF%BC%8Fd%7Bc1%7D%5D%3C%281%2B%EF%BF%A1%29&id=roLbg)且#card=math&code=min%5Bd%7Bc1%7D%EF%BC%8Fd%7Bc2%7D%2Cd%7Bc2%7D%EF%BC%8Fd%7Bc_1%7D%5D%3E%281-%EF%BF%A1%29&id=pfKVj)

如果上述条件满足，不妨设 与X代表的类别相同，算法将调整权向量，使得 输入向量X的方向靠近，而 远离输入向量．调整公式为：

1. %3DW%7Bc_1%7D(old)%2B%5Calpha(X%E2%80%94W%7Bc1%7D(old))#card=math&code=W%7Bc1%7D%28new%29%3DW%7Bc1%7D%28old%29%2B%5Calpha%28X%E2%80%94W%7Bc_1%7D%28old%29%29&id=r1jvW)
2. %3DW%7Bc_2%7D(old)-%5Calpha(X%E2%80%94W%7Bc2%7D(old))#card=math&code=W%7Bc2%7D%28new%29%3DW%7Bc2%7D%28old%29-%5Calpha%28X%E2%80%94W%7Bc_2%7D%28old%29%29&id=zXlX0)

(5) LVQ3算法改进

LVQ3也是同时考虑与输入向量X距离最近的两个权向量 。当条件 (1%2B%EF%BF%A1)#card=math&code=min%5Bd%7Bc_1%7D%EF%BC%8Fd%7Bc2%7D%2Cd%7Bc2%7D%EF%BC%8Fd%7Bc_1%7D%5D%3E%281-%EF%BF%A1%29%281%2B%EF%BF%A1%29&id=DuZAG) 满足时 (￡的一个典型取值为0.2). 权向量将按照下述规则进行调整：

• 如果 两个权向量中有一个对应的分类与输入向量X一致，另一个不一致，则权向量的调整规则同 LVQ2.1
• 如果 代表相同的分类，则权向量 均采用公式 %3DW%7Bc%7D(old)%2B%5Cbeta(X%E2%80%94W%7Bc%7D(old))#card=math&code=W%7Bc%7D%28new%29%3DW%7Bc%7D%28old%29%2B%5Cbeta%28X%E2%80%94W_%7Bc%7D%28old%29%29&id=hx3wf) 进行调整，其中

LVQ3算法通过对标准LVQ算法学习过程的修改，可以使得在网络学习过程不断进行的同时，网络的权向量能够很好地反映输入空间的概率密度分布，并且防止权向量偏离最优的位置。

(6) G-LVQ

G-LVQ将遗传算法应用于LVQ算法中，以克服LVQ算法本身的一些缺陷。

2.1.4 高斯混合聚类(Mixture-of-Gaussian)

高斯混合聚类(Mixture-of-Gaussian)采用概率模型来表达聚类原型.

1. 对于 维样本空间 中的随机向量 ，若 服从高斯分布，则其概率密度函数为 ：
   
   其中 为 维均值向量， 是 的协方差矩阵。 的概率密度函数由参数 决定。
2. 定义高斯混合分布： 。该分布由 个混合成分组成，每个混合成分对应一个高斯分布。其中:
   • 是第 个高斯混合成分的参数。
   • 是相应的混合系数，满足 。
3. 假设训练集 的生成过程是由高斯混合分布给出。
   令随机变量 表示生成样本 的高斯混合成分序号， 的先验概率 。
   生成样本的过程分为两步：
   • 首先根据概率分布 生成随机变量 。
   • 再根据 的结果，比如 ， 根据概率 生成样本。
4. 根据贝叶斯定理， 若已知输出为 ，则 的后验分布为：
   
   其物理意义为：所有导致输出为 的情况中， 发生的概率。
5. 当高斯混合分布已知时，高斯混合聚类将样本集 划分成 个簇 。
   对于每个样本 ，给出它的簇标记 为：
   
   即：如果 最有可能是 产生的，则将该样本划归到簇 。
   这就是通过最大后验概率确定样本所属的聚类。
6. 现在的问题是，如何学习高斯混合分布的参数。由于涉及到隐变量 ，可以采用EM算法求解。
   具体求解参考EM 算法的章节部分。

2.2 基于密度的聚类

k-means算法对于凸性数据具有良好的效果，能够根据距离来讲数据分为球状类的簇，但对于非凸形状的数据点，就无能为力了，当k-means算法在环形数据的聚类时，我们看看会发生什么情况。

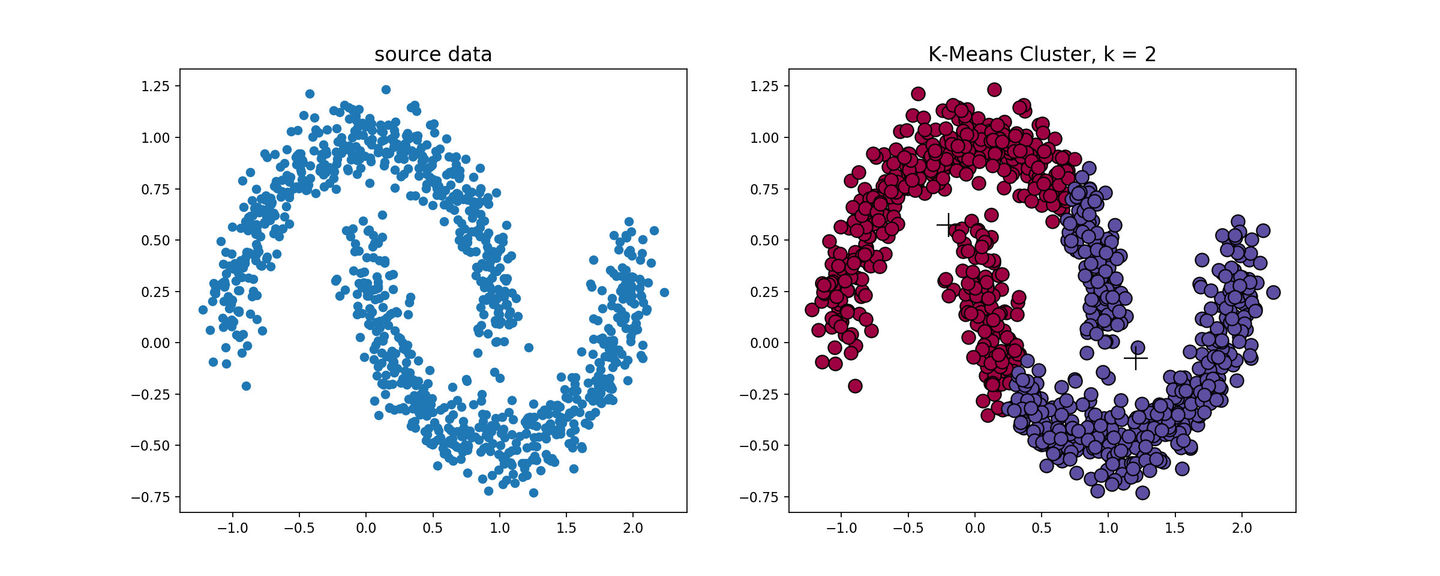
从上图可以看到，kmeans聚类产生了错误的结果，这个时候就需要用到基于密度的聚类方法了。基于密度的聚类(Density-based Clustering)假设聚类结构能通过样本分布的紧密程度确定.密度聚类算法从样本密度的角度来考察样本之间的可连续性，并基于可连续样本不断扩展聚类簇以获得最终的聚类结果.

基于密度的聚类(Density-based Clustering)

• DBSCAN (Density-Based Spatial Clustering of Application with Noise)
• OPTICS (Ordering Points To Identify the Clustering Structure)

2.2.1 DBSCAN

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的空间聚类算法,它不需要定义簇的个数,而是将具有足够高密度的区域划分为簇,并在有噪声的数据中发现任意形状的簇,在此算法中将簇定义为密度相连的点的最大集合。

首先介绍几个概念，考虑集合，表示定义密度的邻域半径，设聚类的邻域密度阈值为，有以下定义：

• 邻域(-neighborhood）

• 密度(desity)的密度为

• 核心点(core-point)
  设，若，则称为的核心点，记中所有核心点构成的集合为，记所有非核心点构成的集合为。
• 边界点(border-point)
  若，且，满足
  
  即的邻域中存在核心点，则称为的边界点，记中所有的边界点构成的集合为。
  此外，边界点也可以这么定义：若，且落在某个核心点的邻域内，则称为的一个边界点，一个边界点可能同时落入一个或多个核心点的邻域。
• 噪声点(noise-point)
  若满足
  
  则称为噪声点。
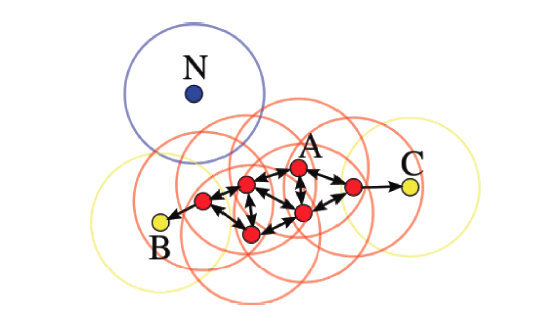
  如下图所示，设，则A为核心点，B、C是边界点，而N是噪声点。

该算法的流程如下：

算法说明:

• DBSCAN算法先任选数据集中的一个核心对象为 “种子 (seed)”,再由此出发确定相应的聚类簇；
• 第1-7行：先根据给定的邻域簇 #card=math&code=%28c%2CMinPts%29&id=BmUqx) 找出所有核心对象；
• 第10-24行：以任一核心对象为出发点，找出由其密度可达的样本生成聚类簇，直到所有核心对象均被访问过为止.

一般来说，DBSCAN算法有以下几个特点：

1. 需要提前确定和值
2. 不需要提前设置聚类的个数
3. 对初值选取敏感，对噪声不敏感
4. 对密度不均的数据聚合效果不好

2.2.2 OPTICS

OPTICS (Ordering Points To Identify the Clustering Structure). OPTICS和DBSCAN聚类相同,都是基于密度的聚类,但是,OPTICS的好处在于可以处理不同密度的类,结果有点像基于连通性的聚类,不过还是有些区别的.

2.3 层次聚类方法

前面介绍的几种算法确实可以在较小的复杂度内获取较好的结果，但是这几种算法却存在一个链式效应的现象，比如：A与B相似，B与C相似，那么在聚类的时候便会将A、B、C聚合到一起，但是如果A与C不相似，就会造成聚类误差，严重的时候这个误差可以一直传递下去。为了降低链式效应，这时候层次聚类就该发挥作用了。

层次聚类(Hierarchical Clustering) 也称为基于连通性的聚类。这种算法试图在不同层次对数据进行划分，从而形成树形的聚类结构。

数据集的划分采用不同的策略会生成不同的层次聚类算法：

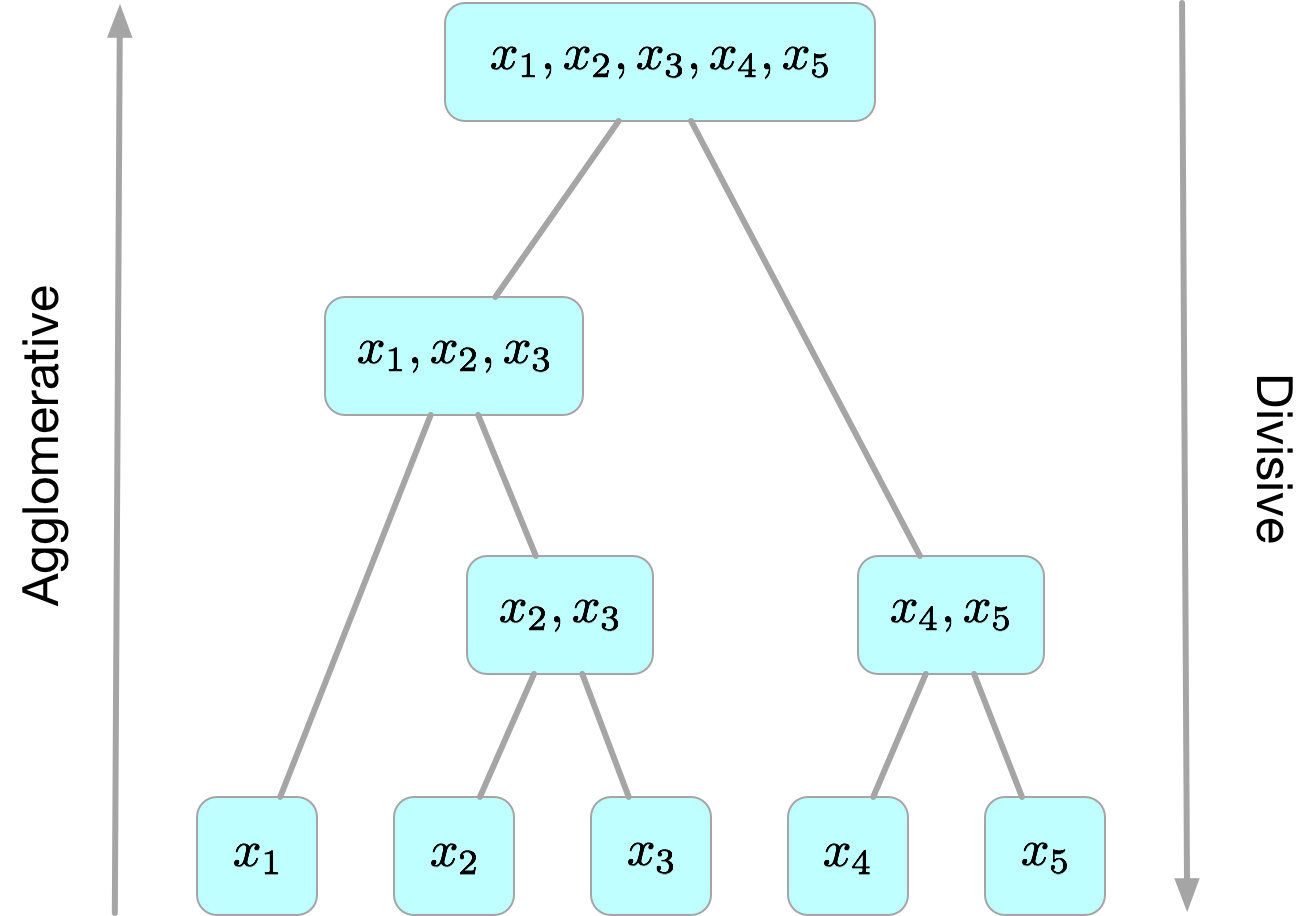
• “自底向上”的聚合策略
  （Agglomerative）。每一个对象最开始都是一个 cluster，每次按一定的准则将最相近的两个 cluster 合并生成一个新的 cluster，如此往复，直至最终所有的对象都属于一个 cluster。这里主要关注此类算法。
  • AGNES(Agglomerative Nesting)
• “自顶向下”的分拆策略
  （Divisive）。最开始所有的对象均属于一个 cluster，每次按一定的准则将某个 cluster 划分为多个 cluster，如此往复，直至每个对象均是一个 cluster。

2.3.1 AGNES

(1) 算法介绍

AGNES(Agglomerative Nesting)是一种采用自底向上聚合策略的层次聚类算法，算法的步骤为：

1. 先将数据集中的每个样本当做是一个初始聚类簇;
2. 然后在算法运行的每一步中找出距离最近的两个点(聚类簇)进行合并为一个聚类簇;
3. 上述过程不断重复，直至所有的样本点合并为一个聚类簇或达到预设的聚类簇个数。 最终算法会产生一棵树，称为树状图(dendrogram), 树状图展示了数据点是如何合并的.

这个算法的关键是如何计算两点之间以及两个聚类簇之间的距离

1. 如何计算两点之间的距离[距离矩阵(Metric)]：
   
2. 如何计算两个聚类簇(集合)之间的距离[链接准则(Linkage criteria)]：

• Complete-linkage clustering(全链接)
• Single-linkage clustering(单链接)
• Mean-linkage clustering(平均链接 UPGMA)
• Centroid-linkage clustering(中心链接 UPGMC)
• Minimum energy clustering

3 聚类效果评价指标

这里给出三个聚类效果评价指标：互信息，标准化互信息，调整互信息(MI, NMI, AMI)

互信息(Mutual information)

互信息的计算公式如下：

标准化互信息(NMI, Normalized Mutual Information)

通常采用NMI和AMI来作为衡量聚类效果的指标。

标准化互信息的计算方法如下：

调整互信息(AMI, Adjusted Mutual Information)

调整互信息的计算要复杂一些，其计算方法如下：

Python实现

Python中的 sklearn 库里有这三个指标的类，可以直接调用；

from sklearn.metrics.cluster import entropy, mutual_info_score, normalized_mutual_info_score, adjusted_mutual_info_score
MI = lambda x, y: mutual_info_score(x, y)
NMI = lambda x, y: normalized_mutual_info_score(x, y, average_method='arithmetic')
AMI = lambda x, y: adjusted_mutual_info_score(x, y, average_method='arithmetic')
A = [1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3]
B = [1, 2, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 1, 1, 3, 3, 3]
#print(entropy(A))
#print(MI(A, B))
print(NMI(A, B))
print(AMI(A, B))
C = [1, 1, 2, 2, 3, 3, 3]
D = [1, 1, 1, 2, 1, 1, 1]
print(NMI(C, D))
print(AMI(C, D))

参考

• 用人话讲明白快速聚类kmeans
• 从零开始教你 KMeans 算法
• 如何正确使用「K均值聚类」？
• K-Means算法之K值的选择
• sklearn入门教程：分类、聚类、回归和降维
• K-means for Beginners: How to Build from Scratch in Python
• Introduction-NLP/chapter/10.文本聚类.md
• 常用聚类算法-知乎
• Clustering.pdf
• citisy的炼丹房
• LVQ学习向量量化算法原理以及代码实现-雪球
• LVQ聚类算法
• 机器学习基础（八）- 聚类笔记
• SOM算法、LVQ算法及其变体综述