2022-05-06-[ML]-AE vs. VAE vs. DAE

转载自《AutoEncoder (AE) 和 Variational AutoEncoder (VAE) 的详细介绍和对比》

数据压缩

数据压缩可以使用更少的维度表示相同数量的信息。 这助于解决维度诅咒的问题，还可以部分的解决过拟合的现象。 所以在一般情况下我们都会在数据集用于训练之前，对其使用降维方法进行处理。
这就是自动编码器 (AE) 和变分自动编码器 (VAE) 发挥作用的地方。 它们是用于压缩输入数据的端到端网络。 Autoencoder 和 Variational Autoencoder 都用于将数据从高维空间转换到低维空间，从本质上实现压缩。

Autoencoder - AE

自编码器（AE）用于学习对给定网络配置的无标记数据的有效嵌入。自编码器由两部分组成，编码器和解码器。 编码器将数据从高维空间压缩到低维空间（也称为潜在空间），而解码器则相反，即将潜在空间转换回高维空间。 解码器用于确保潜在空间可以从数据集空间中捕获大部分信息，解码器则以潜在空间输出作为输入判断能否完整的还原数据。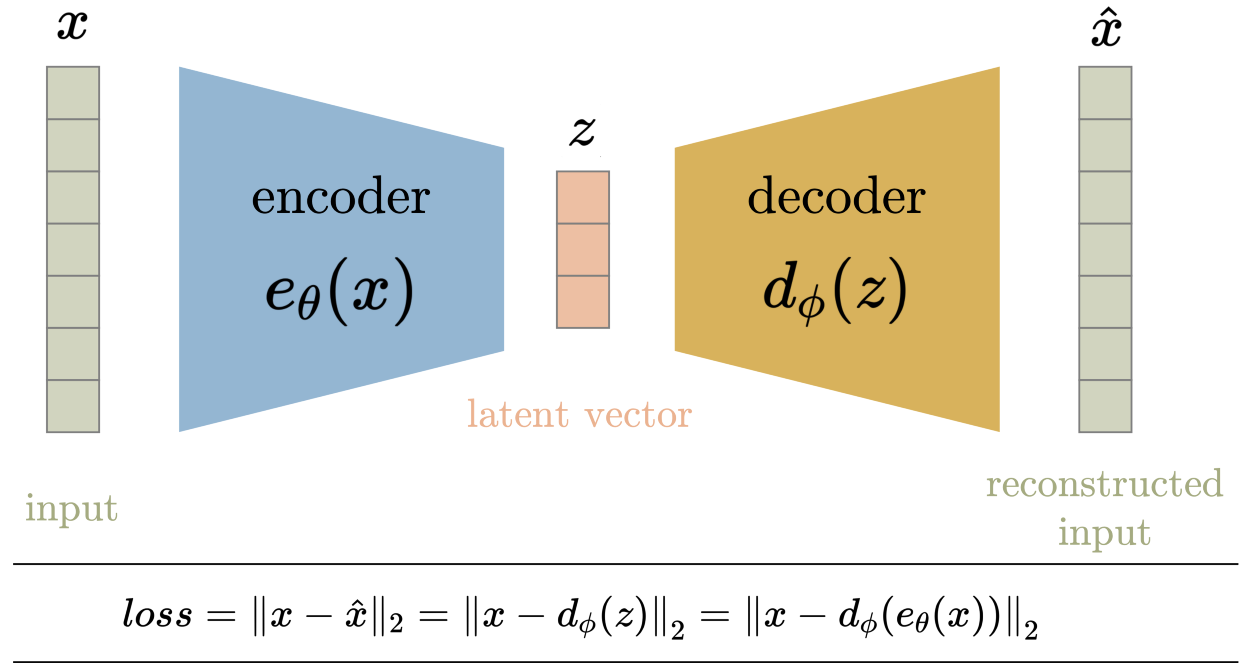

在训练过程中，输入数据x被输入到编码器函数e_theta(x)。输入通过一系列层(由变量theta参数化)来减少其维数，从而得到压缩的潜在向量z。层的数量、层的类型和大小，以及潜在空间维数都是可设置的超参数。如果潜在空间的维数小于输入空间的维数，则实现压缩（从根本上消除了冗余属性）。
解码器d_phi(z)通常(但不是必须)由编码器中使用的层的近似互补层组成，但顺序相反。一层中的近补层可以用来撤销(在某种程度上)原始层的操作，例如转置conv层到conv层、池化到反池化，全连接到全连接等。

损失函数

整个编码器-解码器架构在同一损失函数上共同训练，损失函数鼓励在输出端重建输入。 所以一般情况下使用的损失函数是编码器输入和解码器输出之间的均方误差。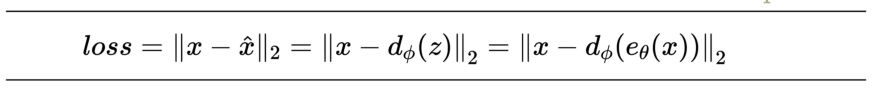

这个想法理论支持是有一个低维的潜在空间，能够达到最大压缩，但同时使复原后的数据误差足够小。 将潜在空间的维数降至这一数值下则会导致大量的信息丢失。
AE对潜在空间的值/分布没有限制，只要它可以在解码器通过它时重建输入保证足够小的误差即可。

潜在的空间可视化

下面是在MNIST数据集上训练网络生成的潜在空间的示例。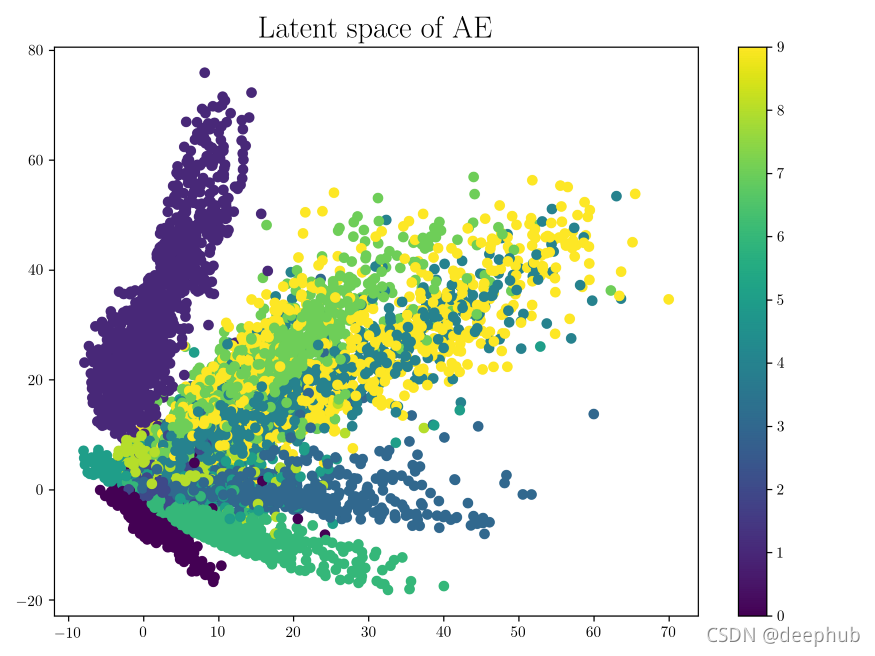

可以看出，相同的数字倾向于将自己聚集在相近的潜在空间中。 另一个需要注意的是，潜在空间的某些部分与任何数据点都不对应。 使用这些作为编码器的输入将导致输出看起来不像 MNIST 数据中的任何数字。 这就是我们所说的潜在空间没有正则化的意思。 这样的潜在空间只有少数具有生成能力的区域/簇，这意味着对潜在空间中簇内的任何点进行采样都会生成与该簇相关的变量， 但是整个潜在空间并不都具备生成能力。 不属于任何簇的区域将产生垃圾输出。 一旦网络被训练，并且训练数据被移除，我们就无法知道解码器从一个随机采样的潜在向量产生的输出是否有效。因此AE主要用于压缩。
对于有效输入，AE 能够将它们压缩到更少的维度，基本上消除了冗余，但由于潜空间AE是非正则化的，解码器不能用于从潜空间采样的向量生成有效的输入数据。

为什么使用AE压缩?

线性自编码器的潜在空间与数据主成分分析（PCA）的特征空间非常相似。如果AE与PCA相似，为什么要使用AE?AE 的强大之处在于它的非线性。 添加非线性（例如非线性激活函数和更多隐藏层）使 AE 能够在较低维度上学习相当强大的输入数据表示，而信息丢失要少得多。

Variational AutoEncoders - VAE

变分自编码器（VAE）解决了自编码器中非正则化潜在空间的问题，并为整个空间提供了生成能力。 AE 中的编码器输出潜在向量。VAE的编码器不输出潜空间中的向量，而是输出每个输入的潜空间中预定义分布的参数。然后VAE对这个潜在分布施加约束，迫使它成为一个正态分布。这个约束确保了潜在空间是正则化的。
VAE的架构图如下所示。在训练过程中，输入数据x被输入到编码器函数。就像AE一样，输入通过一系列层(由超参数控制)来减少其维度，以获得压缩的潜在向量z。但是潜在向量不是编码器的输出。编码器输出每个潜在变量的平均值和标准差。然后从这个平均值和标准偏差中采样潜在向量，然后将其输入到解码器中重建输入。VAE中解码器的工作原理与AE中解码器相似。

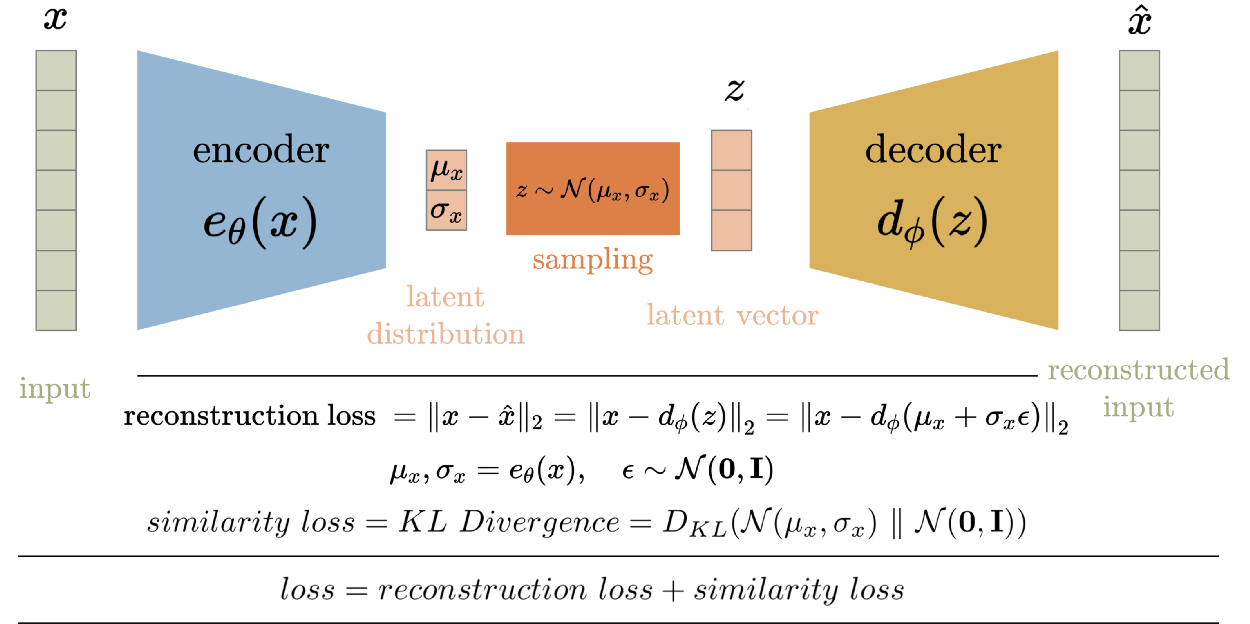
损失函数

损失函数由VAE目标定义。VAE有两个目标

• 重建的输入
• 潜空间应为正态分布

因此，将VAE的训练损失定义为重构损失和相似损失之和。重构误差，就像AE中一样，是输入输出和重构输出的均方损失。相似性损失是潜空间分布与标准高斯(零均值和单位方差)之间的KL散度。因为此损失函数是这两个损失的总和。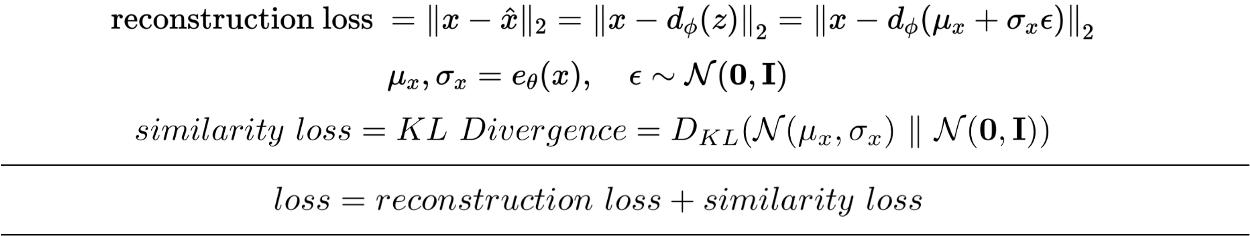

如前所述，在将潜在向量发送到解码器之前需要从编码器生成的分布中采样。 这种随机采样使得编码器很难进行反向传播，因为我们无法追溯由于这种随机采样而导致的错误。因此，我们使用重参数的方法（reparameterization trick）来模拟采样过程，这使得错误可以通过网络传播。 潜在向量 z 表示为编码器输出的函数。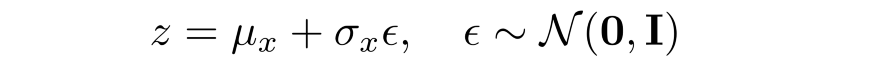

潜在空间可视化

模型的训练过程试图在两个损失之间找到平衡，最终得到一个潜在空间分布，看起来像单位范数，集群对相似的输入数据点进行分组。 单位范数条件确保潜在空间均匀分布并且簇之间没有显着间隙。 事实上，相似数据输入的集簇通常在某些区域重叠。 下面是通过在相同的 MNIST 数据集上训练网络生成的潜在空间的示例，用于可视化 VAE 的潜在空间。 请注意簇之间没有间隙，空间类似于单位范数的分布。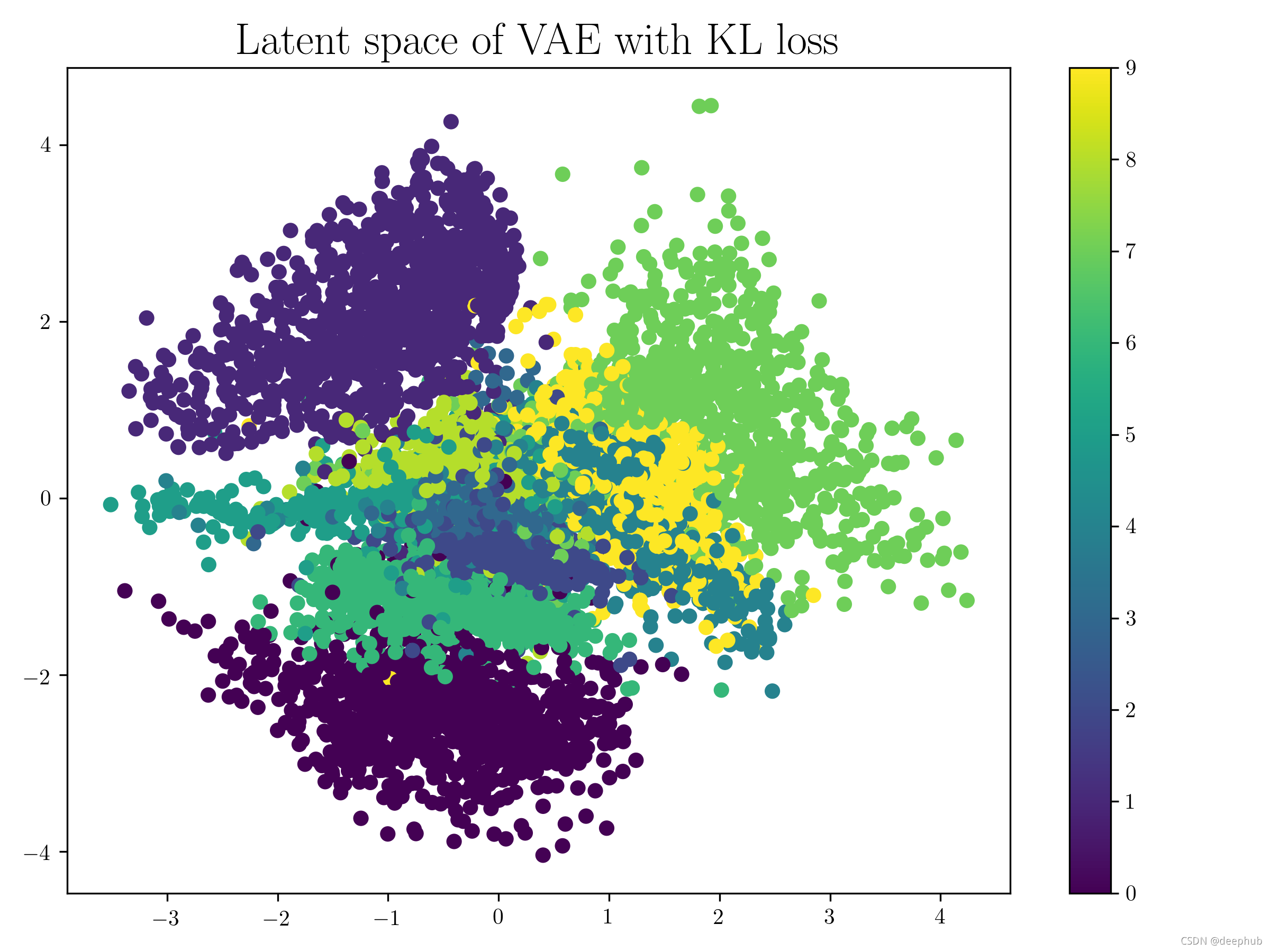

需要注意的重要一点是，当从具有重叠簇的区域中采样潜在向量时，我们会得到变形数据。 当我们对从一个簇移动到另一个簇的潜在空间进行采样时，我们得到的是解码器输出之间的平滑过渡。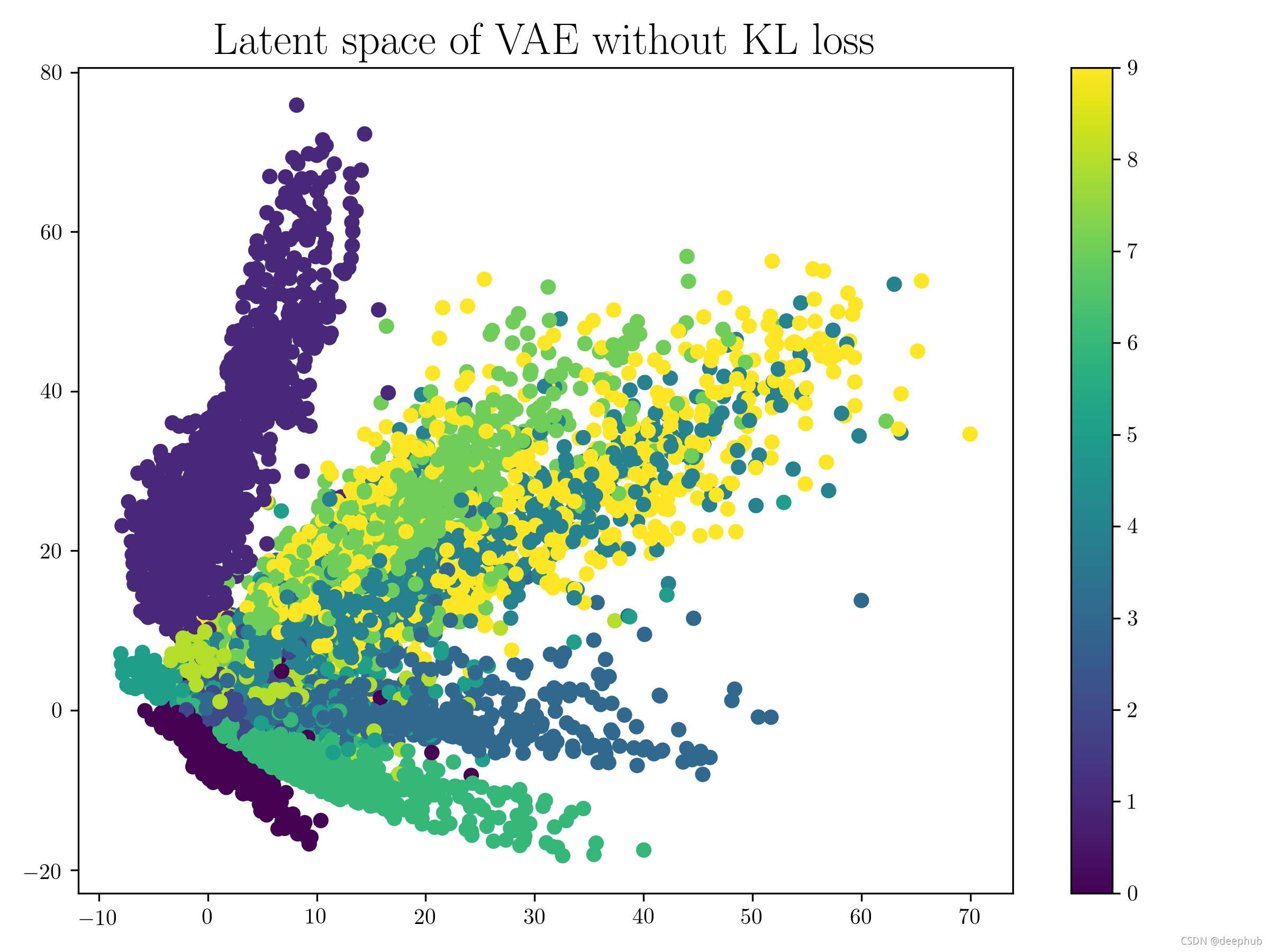

我们可以看到如果不使用KL散度，则跟AE模型差不多。

Denoising Autoencoder

降噪自编码器（DAE）是另一种自编码器的变种。强烈推荐 Pascal Vincent 的论文，该论文很详细的描述了该模型。降噪自编码器认为，设计一个能够恢复原始信号的自编码器未必是最好的，而能够对 “被污染/破坏” 的原始数据进行编码、解码，然后还能恢复真正的原始数据，这样的特征才是好的。
从数学上来讲，假设原始数据 x 被我们“故意破坏”了，比如加入高斯噪声，或者把某些维度数据抹掉，变成 x’，然后在对 x’ 进行编码、解码，得到回复信号 xx = g(f(x’)) 。该恢复信号尽可能的逼近未被污染的原数据 x 。此时，监督训练的误差函数就从原来的 L(x, g(f(x))) 变成了 L(x, g(f(x’)))。
从直观上理解，降噪自编码器希望学到的特征尽可能鲁棒，能够在一定程度上对抗原始数据的污染、缺失等情况。Vincent 论文里也对 DAE 提出了基于流行学习的解释，并且在图像数据上进行测试，发现 DAE 能够学出类似 Gabor 边缘提取的特征变换。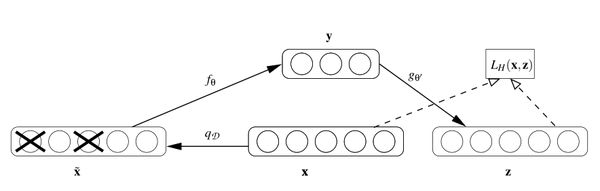

总结

本文对 Autoencoder (AE) 和variational Autoencoder (VAE) 进行了详细的介绍，它们分别是主要用于数据压缩和数据生成。 VAE 解决了 AE 的非正则化潜在空间的问题，这使其能够从潜在空间中随机采样的向量生成数据。以下是 AE和VAE的关键点总结:

自编码器 (AE)

• 用于在潜在空间中生成输入的压缩变换
• 潜变量没有被正则化
• 选择一个随机的潜在变量可能会产生垃圾输出
• 潜变量具有不连续性
• 潜在变量是确定性值
• 潜在空间缺乏生成能力

变分自编码器 (VAE)

• 将潜在变量的条件强制为单位范数
• 压缩形式是潜在变量的均值和方差
• 潜在变量是平滑连续的
• 潜在变量的随机值在解码器产生有意义的输出
• 解码器的输入是从具有编码器输出均值和方差的高斯中采样的随机值。
• 正则化的潜在空间
• 潜在空间具有生成能力