title: LambdaMART二次深入理解
subtitle: LambdaMART
date: 2021-04-20
author: NSX
catalog: true
tags:
- LambdaMART
在本文中,我们将深入讨论我们选择的模型:LambdaMART:
- 提升(简而言之):利用梯度提升树的理论和实际效益
- LambdaMART 是如何工作的?Pairwise 学习,NDCG 调整权重,解决表现偏差
- 将 LambdaMART 对“期望盈利能力”进行排序
- 关于特征工程的一些讨论
- 为什么不是隐语义模型?
LambdaMART 的优点
我们选择 LambdaMART 的核心原因是:
- 灵活的数据输入。作为一个梯度提升树,LambdaMART 接受任何浮点数据作为输入,允许缺失值,不需要数据标准化。只有类别变量不能被自动转换为浮点数,但是具有低基数的变量可以映射到整数。因此,我们唯一不能包含的数据是酒店 id 和用户 id,因为它们的基数太高。
- 强大的函数逼近能力。梯度提升树理论上是一个通用的函数逼近器。在实践中,这不会是真的,但梯度提升树的性能仍几乎无与伦比,只要特征集可以对于因变量可以形成有意义的描述。
- 易于实现。
xgboost包有一个高度优化的 LambdaMART 实现,它允许我们用一行代码在几分钟内原型化模型。 - 有意义的得分函数。下一节将解释,模型得分可以通过一个 softmax 或指数函数来表示一家酒店相对于另一家酒店的预订可能性。这让我们能够根据酒店的预期盈利能力对它们进行有意义的重新排序。
- 可解释的预测。该模型做出的每一个预测都可以用 SHAP 值来解释,我们在前一篇文章中提到过。
如果不首先理解 LambdaMART 在做什么,就很难扩展这些要点,所以我们将简要地介绍一下模型的结构。
对 LambdaMART 了解的更清楚一些

因为 LambdaMART 方法经过了多年的改进,所以符号是不一致的,并且很大程度上集中在高效计算上,我们把这个问题留给了 xgboost。因此,我们的解释从头开始,重点放在对我们的用例很重要的核心思想上。
LambdaMART 中的 MART,非常简短
在它的核心,LambdaMART 是一个损失函数(“Lambda”)附加到一个梯度提升森林(“MART” — 多重加法回归树)上。梯度提升森林通过训练一棵新树来预测之前出现的树的误差(损失函数的“梯度”)来改进它的预测。预测是通过将第一棵树的原始估计值与后续树的所有修正值相加而得出的。
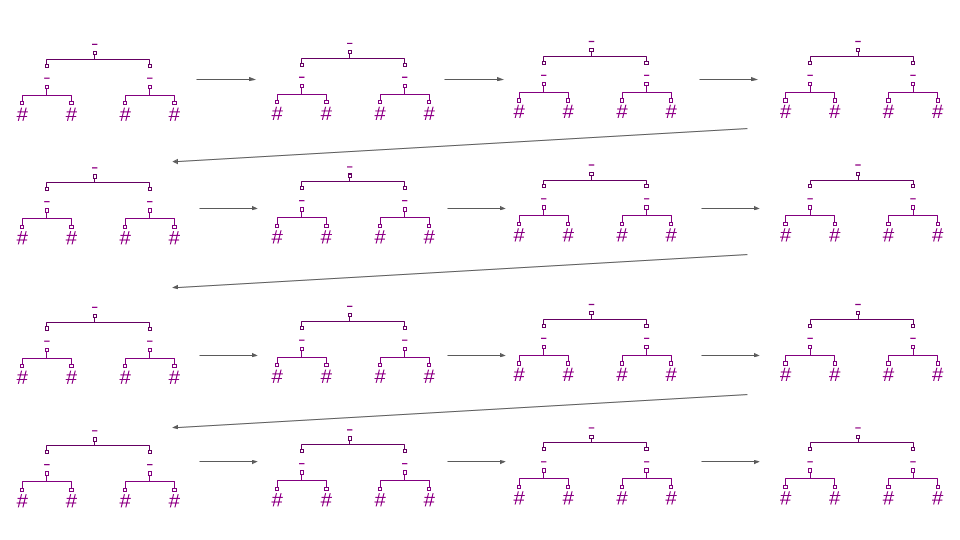
由于树不会像线性回归那样对模型函数空间施加强大的结构,LambdaMART 实现良好排名的能力几乎完全取决于其“Lambda”误差的质量。由于这个原因,损失函数可以被详细的解释。
LambdaMART 的损失
Lambda 损失要求某些搜索结果的得分高于其他搜索结果。例如,预订的酒店应该比只被点击的酒店得分高,而被点击的酒店应该比完全被用户忽略的酒店得分高。使这些 pairwise 的比较是 Lambda 梯度函数的核心。
更精确地说,给定酒店和分数 I,酒店和分数 J,Lambda 梯度估计的酒店优于酒店的概率为σ(J-I),其中σ是 sigmoid 函数。sigmoid 通常使用 e=2.7182818…,但是 Lambda 训练过程实际上对 sigmoid 的 base 是不变的。
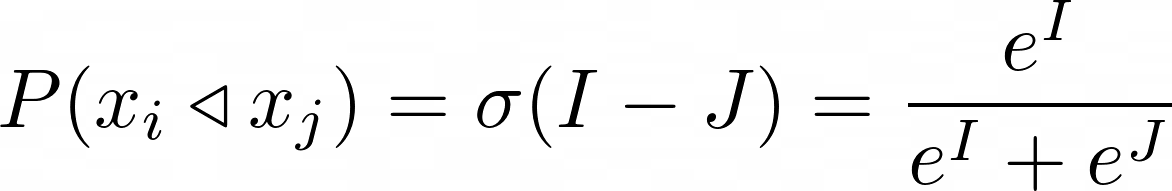
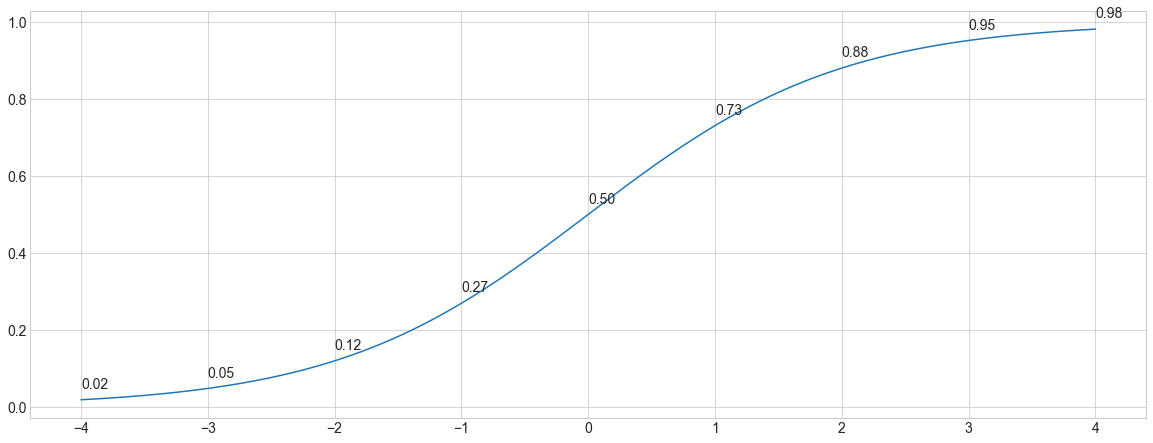
x_i比 x_j的优先的概率代表什么?以下是几种解释:
- 酒店x_i被点击或订购的次数比x_j大。
- 酒店x_i被选中的条件概率,假如只有x_i和x_j两个酒店,这两个酒店中只有一个被选中。
我们希望将我们估算的 pairwise 偏好概率与我们排名中所有酒店对(x_i, x_j)的真实偏好概率之间的距离最小化:
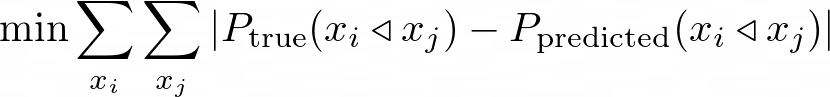
使用这样的 pairwise 损失,我们就能训练出一个像样的模型。然而,我们可以考虑两个额外的效应来获得更好的性能:
并不是所有的酒店对都是一样的:例如,我们并不关心排名第 340 位和第 341 位的酒店交换模式,而是关心排名第 1 位和第 341 位的酒店交换模式。如果上面的排名更正确,那么下面的一些错误排名是可以接受的。
点击数据有偏差:排名高的结果更容易被观察到(表示偏差),即使被观察到了,排名高的结果也更容易被点击(信任偏差)。考虑到这一点,排名较高的结果应该是有问题的。
我们依次来看。
使用 NDCG-weighting 调整 listwise 损失
高排名的结果相比低排名的结果的重要性通过 NDCG 来进行度量。下面显示了 NDCG 的一个表达式,其中 IDCG 是排序所能达到的理想或最大 DCG, rel_i是排在第 i 个的搜索结果的相关性标签值。

NDCG 是唯一的排名指标,可以区分出两个排序中哪个是更好的一个。除此之外,它对你的直觉几乎毫无用处。随着搜索结果数量的增加,搜索请求的预期 NDCG 收敛到 0,因此用不同的基数比较两个搜索请求的 NDCGs 是不合适的。
我们可以看到,当相关结果的排名较差时,DCG 分数会下降,因为贡献的分数被一个对数因子打折了。NDCG 为 99 个不相关的结果(相关标签为 0)和 1 个相关的结果(相关标签为 1)的搜索请求进行评分,下面是每一个可能的排序的相关结果图。
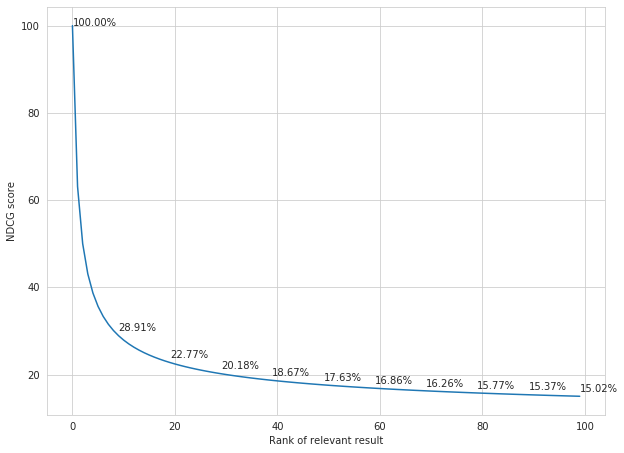
给于高排名对比低排名对更高的权重,每一对(xi, x_j)通过ΔNDCG 来加权,这个差值为 NDCG 分数和交换之后的 NDCG 分数之间的绝对差。
例如,如果相关结果排在第 1 位,它的 NDCG 值为 1,而如果与排在第 100 位的无关结果进行交换,NDCG 值为。1502。那一对排序(1, 100)的 NDCG 的变化为 |1-0.1502|=|0.8498|。
使用反向加权来去除点击数据的偏差
表示偏差影响用户查看搜索结果的概率。如果一个搜索结果的排名靠后,那么用户看到它的几率就会降低。信任偏差会影响一个搜索结果被点击的概率,即使它被用户看过。虽然这是两种不同的效果,但它们都可以根据搜索结果的排名改变其被点击的概率。我们通过估计每个位置i上的两个量来衡量这种效果:
- 本文地址:为什么我们选择 LambdaMART 作为我们的酒店排序模型
- 本文版权归作者和AIQ共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出
- 正偏好比 p+(i),搜索结果如果排在其他的位置相对于它在第 i 位的时候,点击率的比例。例如,如果 rank 1 是参考点,rank 2 的正偏好比例是 0.25,那么我们期望一个搜索结果在 rank 2 的时候被点击次数是排在 rank 1 的 25%。在这个例子里,第一位的正偏好比例一般是 1。
- 负偏好比 p-(i),或倒数是不相关的,如果它占据其他一些里程碑的排名。例如,如果 rank 1 是参考点,而 rank 2 的负偏好比是 4,那么我们就会认为未被点击的 rank 2 的搜索结果的不相关性是未被点击的 rank 1 的搜索结果的 4 倍。
p+(i) 和 p-(i) 对于所有的排序位置 i 在 LambdaMART 训练过程中都是可迭代估计的,使用下面一组方程。其中,L(i, j)是原始(有偏差的)的 pairwise 损失函数,p* 这一项是在前一次迭代中估计出来的,然后对所有的查询 q 和搜索结果 j 加起来。
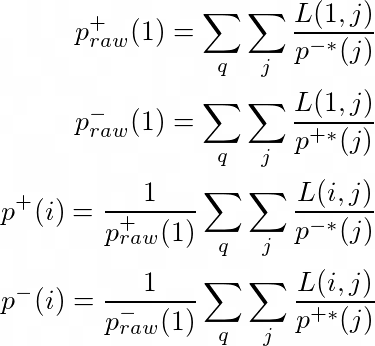
表现偏差的影响可以通过简单地用损失除以偏差来逆转。这个修正给了我们一个一致的和无偏的 pairwise 的损失。

Unfortunately, I discovered inverse propensity weighting while writing this blog post. Fortunately, at time of writing, no well-maintained gradient boosting library had an implementation of inverse propensity debiasing, so my ignorance didn’t actually make a difference. An implementation of a neural network architecture was released during the writing of this blog post.
把所有的组合起来
搜索结果x_i的 Lambda 梯度很简单,就是这些加权的 NDCG 全部加起来,就是对于每一对 (x_i, x_j)的修正了偏差的 pairwise 误差。注意,使用了相同的 label 的结果在交换的时候在 NDCG 上没有变化,所以,大部分的值是 0.方程如下:

偏好概率的校准度量
我之前说过 LambdaMART 估计了 i 优于 j 的偏好概率。这是一个相当强的声明,特别是当 loss 函数包含 NDCG-weighting 的时候。然而,下面的图表显示,该模型是根据经验进行了概率估计校准的。为了进行校准,酒店 i,模型估计有 p% 的概率优于某个酒店 j 被选中(在 x 轴上),需要实际被选中的概率为 p%(在 y 轴上)。
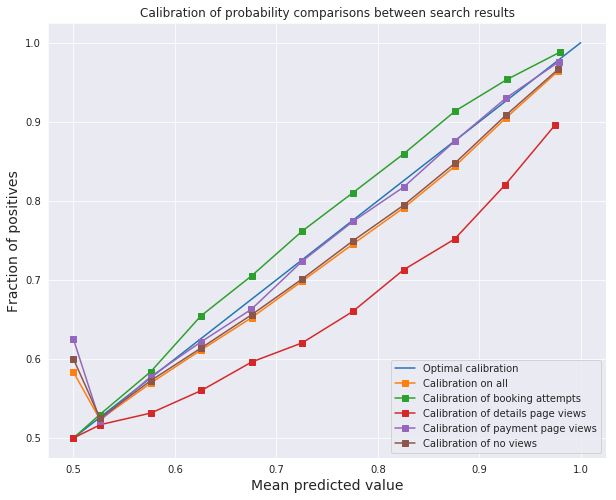
原始 Lambda 论文还对使用 Lambda 梯度训练的神经网络模型参数的小扰动导致训练集上的期望 NDCG 较低进行了数值观察,表明该模型在拟合偏好概率的同时,联合最大化了 NDCG。同时做两件事情的能力都意味着 NDCG 最大化和最小化的目标偏好概率损失没有强烈的相互冲突,所以我们可以鱼(校准概率)和熊掌(NDCG 加权)兼得。

