2022-06-23-EM 算法

EM算法也称期望最大化（Expectation-Maximum，简称EM）算法，它是一个基础算法，是很多机器学习领域的基础，比如隐式马尔科夫算法（HMM），LDA主题模型的变分推断算法等等。

似然函数(likelihood function)

在机器学习中，似然函数是一种关于模型中参数的函数。“似然性(likelihood)”和”概率(probability)“词意相似，但在统计学中它们有着完全不同的含义：概率用于在已知参数的情况下，预测接下来的观测结果；似然性用于根据一些观测结果，估计给定模型的参数可能值。

Probability is used to describe the plausibility of some data, given a value for the parameter. Likelihood is used to describe the plausibility of a value for the parameter, given some data.

其数学形式表示为：假设 X 是观测结果序列，它的概率分布 依赖于参数 θ，则似然函数表示为：

对数似然(log likelihood)

由于对数函数具有单调递增的特点，对数函数和似然函数具有同一个最大值点。取对数是为了方便计算极大似然估计，MLE中直接求导比价困难，通常先取对数再求导，找到极值点。对数函数如下图红线所示：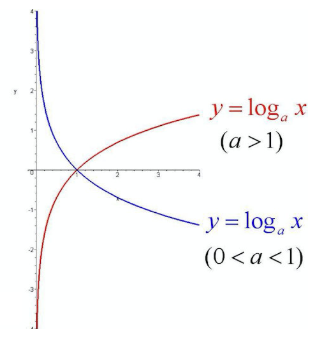

负对数似然(negative log-likelihood)

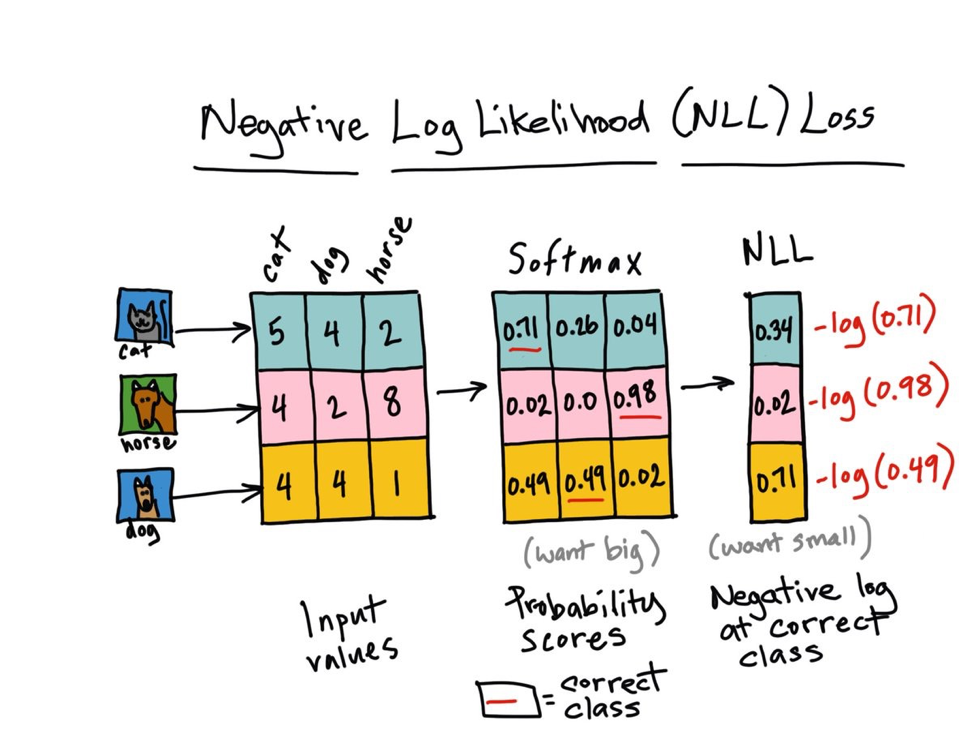
实践中，softmax函数通常和负对数似然(negative log-likelihood,NLL)一起使用，这个损失函数非常有趣，如果我们将其与softmax的行为相关联起来一起理解。首先，让我们写下我们的损失函数:

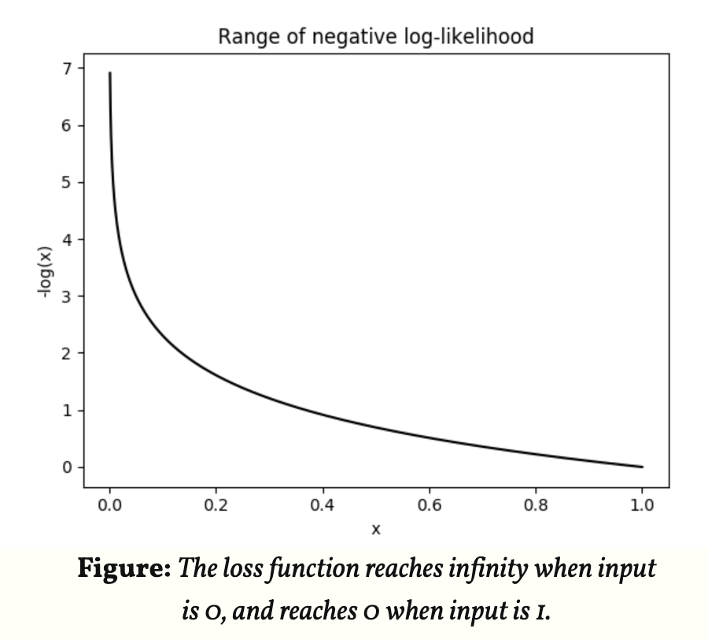
回想一下，当我们训练一个模型时，我们渴望能够找到使得损失函数最小的一组参数(在一个神经网络中，参数指权重weights和偏移biases)。由于是对概率分布求对数，概率p的值为，取对数后为红色线条在 [0,1] 区间中的部分，再对其取负数，得到负对数似然函数如下左图所示：

我们希望得到的概率越大越好，因此概率越接近于1，则函数整体值越接近于0，即使得损失函数取到最小值。

最大似然估计(Maximum Likelihood Estimation,MLE)

假设每个观测结果 x 是独立同分布的，通过似然函数求使观测结果 X 发生的概率最大的参数，即。在“模型已定，参数未知”的情况下，使用最大似然估计算法学习参数是比较普遍的。

要求出，只需要使的似然函数极大化，然后极大值对应的就是我们的估计。这里就回到了求最值的问题了。怎么求一个函数的最值？当然是求导，然后令导数为零，那么解这个方程得到的就是了（前提是函数连续可微）。那如果是包含多个参数的向量，那么如何处理呢？当然是求对所有参数的偏导数，也就是梯度了，那么 n 个未知的参数，就有 n 个方程，方程组的解就是似然函数的极值点了，当然就得到了这 n 个参数了。

• 最大似然数学问题示例（100名学生的身高问题）
  • 样本集
  • 概率密度：抽到男生i（的身高）的概率
  • 是服从分布的参数
  • 独立同分布：同时抽到这100个男生的概率就是他们各自概率的乘积
  • 最大似然函数：（对数是为了乘法转加法）
  • 什么样的参数能够使得出现当前这批样本的概率最大
  • 已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，
    参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。

所以，其实最大似然估计你可以把它看做是一个反推。多数情况下我们是根据已知条件来推断结果，而最大似然估计是已经知道了结果，然后寻找使该结果出现的可能性最大的条件，以此作为估计值。

比如，如果其他条件一定的话，抽烟者发生肺癌的危险是不抽烟者的五倍，那么如果我们知道有个人是肺癌，我想问你这个人是抽烟还是不抽烟。你如何判断，你可能对这个人一无所知，你所知道的只有一件事，那就是抽烟更容易发生肺癌，那么你会猜测这个人不抽烟吗？我相信你更可能会说，这个人抽烟，为什么？这就是“最大可能”，我只能说他“最有可能”是抽烟的，“他是抽烟的”这一估计才是“最有可能”得到“肺癌” 这样的结果，这就是最大似然估计。

总结一下：极大似然估计，只是概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次实验，观察其结果，利用结果推出参数的大概值。极大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆把这个参数作为估计的真实值。

极大似然估计的一般步骤如下:
(1) 写出似然函数;
(2) 对似然函数取对数，得到对数似然函数;
(3) 求对数似然函数的关于参数组的偏导数，并令其为0，得到似然方程组;
(4) 解似然方程组，得到参数组的值.

EM-期望最大算法

【机器学习】EM——期望最大（非常详细）

EM 算法，全称 Expectation Maximization Algorithm。期望最大算法是一种迭代算法，用于含有隐变量（Hidden Variable）的概率参数模型的最大似然估计或极大后验概率估计。

思想

有时候因为样本的产生和隐含变量有关（隐含变量是不能观察的），而求模型的参数时一般采用最大似然估计，由于含有了隐含变量，所以对似然函数参数求导是求不出来的，这时可以采用EM算法来求模型的参数的（对应模型参数个数可能有多个），EM算法一般分为2步：

• E步：选取一组参数，求出在该参数下隐含变量的条件概率值；
• M步：结合E步求出的隐含变量条件概率，求出似然函数下界函数（本质上是某个期望函数）的最大值。

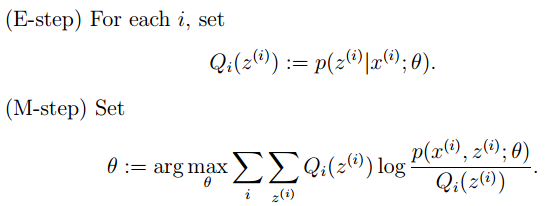
关于EM算法可以参考Ng的cs229课程资料 或者网易公开课：斯坦福大学公开课 ：机器学习课程。

举例

1 背景

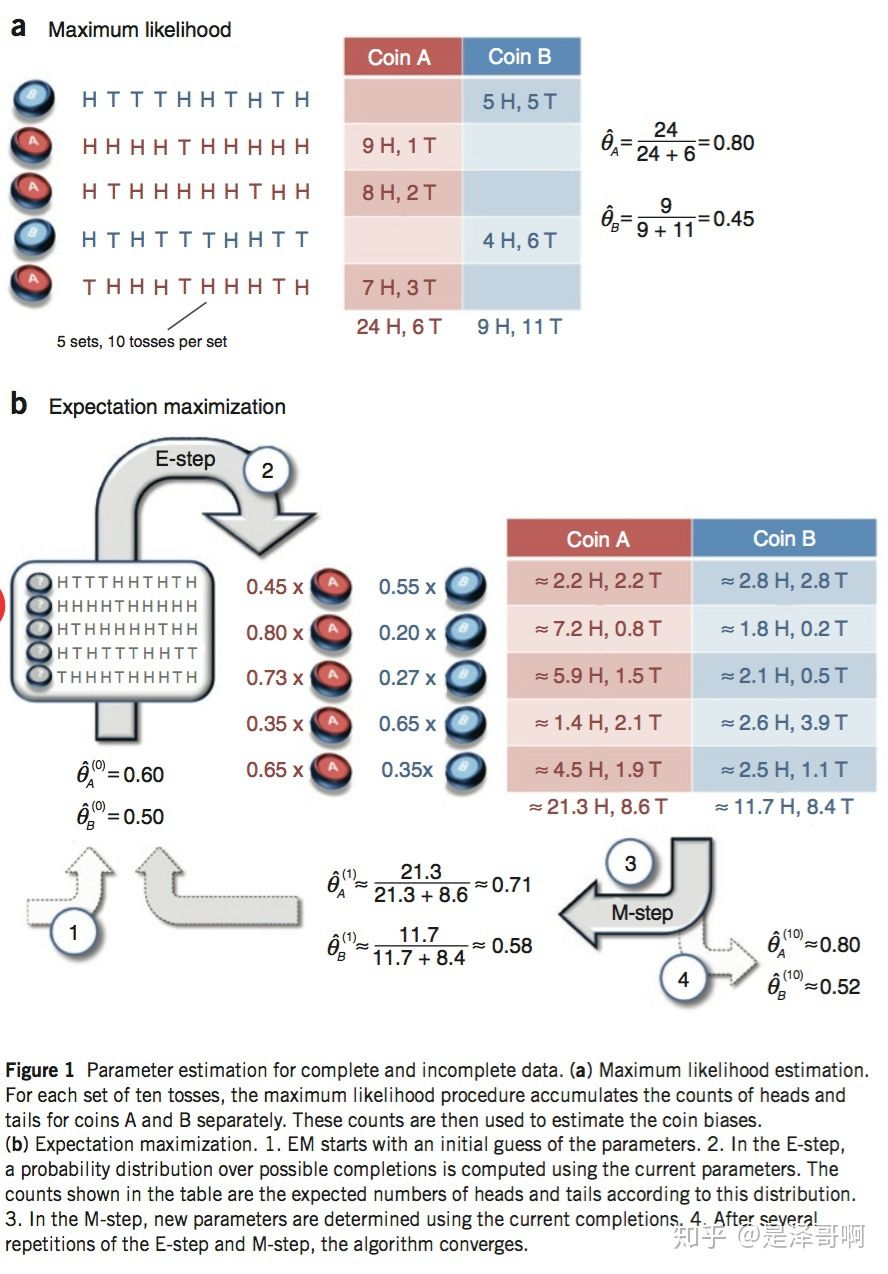
我们将引用 Nature Biotech 的 EM tutorial 文章中的例子。假设有两枚硬币 A 和 B，他们的随机抛掷的结果如下图所示：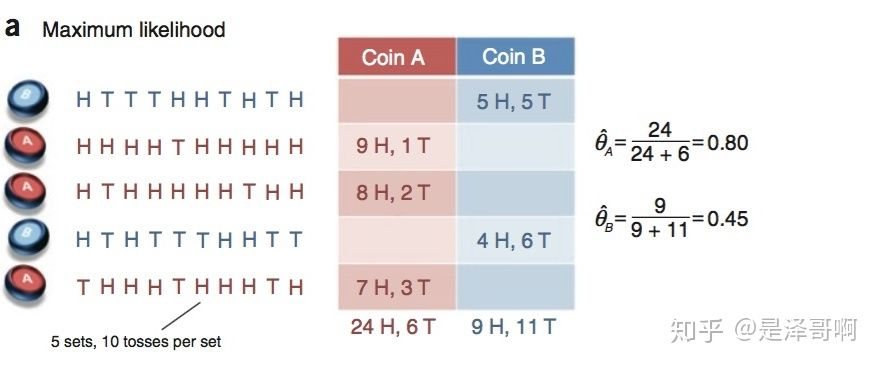

我们很容易估计出两枚硬币抛出正面的概率：

现在我们加入隐变量，抹去每轮投掷的硬币标记：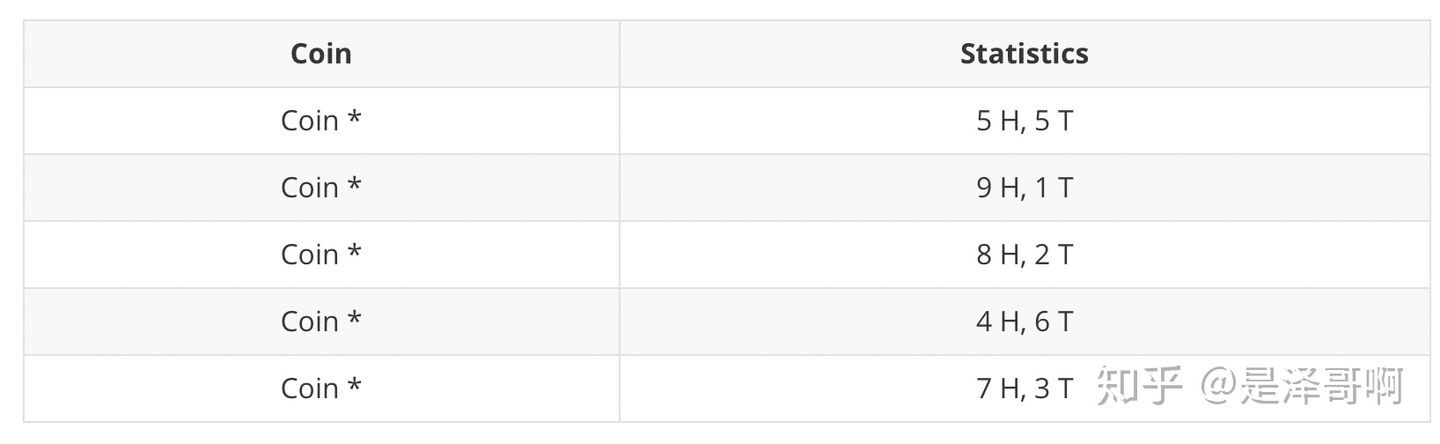

碰到这种情况，我们该如何估计和的值？

我们多了一个隐变量 ，代表每一轮所使用的硬币，我们需要知道每一轮抛掷所使用的硬币这样才能估计和的值，但是估计隐变量 Z 我们又需要知道和的值，才能用极大似然估计法去估计出 Z。这就陷入了一个鸡生蛋和蛋生鸡的问题。

其解决方法就是先随机初始化和，然后用去估计 Z， 然后基于 Z 按照最大似然概率去估计新的和，循环至收敛。

2 计算

随机初始化 和
对于第一轮来说，如果是硬币 A，得出的 5 正 5 反的概率为： ；如果是硬币 B，得出的 5 正 5 反的概率为： 。我们可以算出使用是硬币 A 和硬币 B 的概率分别为：


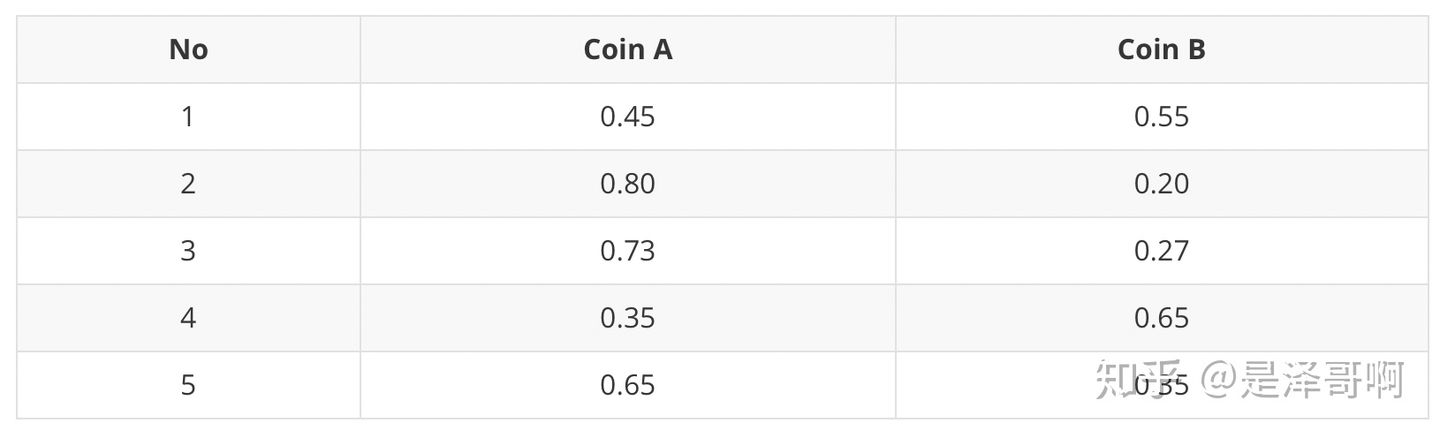
从期望的角度来看，对于第一轮抛掷，使用硬币 A 的概率是 0.45，使用硬币 B 的概率是 0.55。同理其他轮。这一步我们实际上是估计出了 Z 的概率分布，这部就是 E-Step。

结合硬币 A 的概率和上一张投掷结果，我们利用期望可以求出硬币 A 和硬币 B 的贡献。以第二轮硬币 A 为例子，计算方式为：

于是我们可以得到：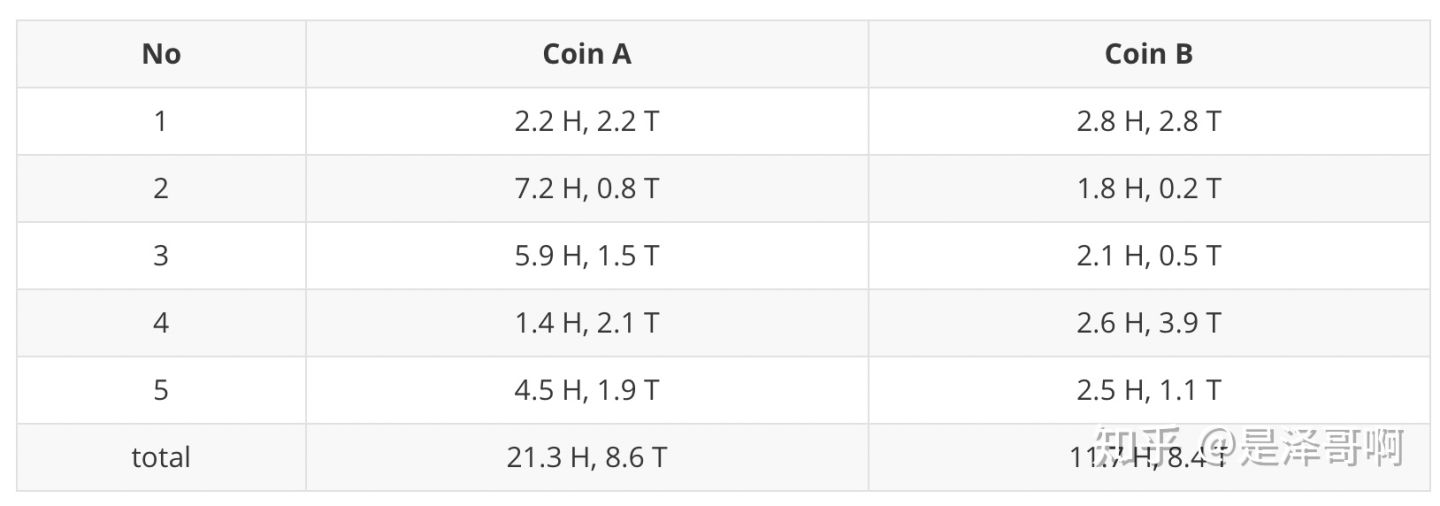

然后用极大似然估计来估计新的 和 。

这步就对应了 M-Step，重新估计出了参数值。
如此反复迭代，我们就可以算出最终的参数值。

上述讲解对应下图：

参考

• Nature Biotech在他的一篇EM tutorial文章《Do, C. B., & Batzoglou, S. (2008). What is the expectation maximization algorithm?. Nature biotechnology, 26(8), 897.》中，用了一个投硬币的例子来讲EM算法的思想。