理论基础
NLP的生成任务一般是要生成一个序列,那么在生成序列的过程中,每一步都能够计算出当前位置所有单词的概率,而通过这个概率选择单词,就可以看做是在解码。当然,t时刻生成的单词概率,会受到t-1时刻选择结果的影响。因此不同的解码方法,会带来不同的结果。Beam Search是一种宽度受限的搜索方法,常用于NLP的生成任务,用在解码端。常用的解码策略如下:
贪心搜索(Greed Search)
贪心搜索的思想非常简单,生成序列的每一步,都选择概率最大的那个单词 (即 argmax)。将其用作下一个单词,并在下一步中将其作为输入提供。继续前进,直到产生
贪心搜索由于缺乏回溯,输出可能很差 (例如,不合语法,不自然,荒谬)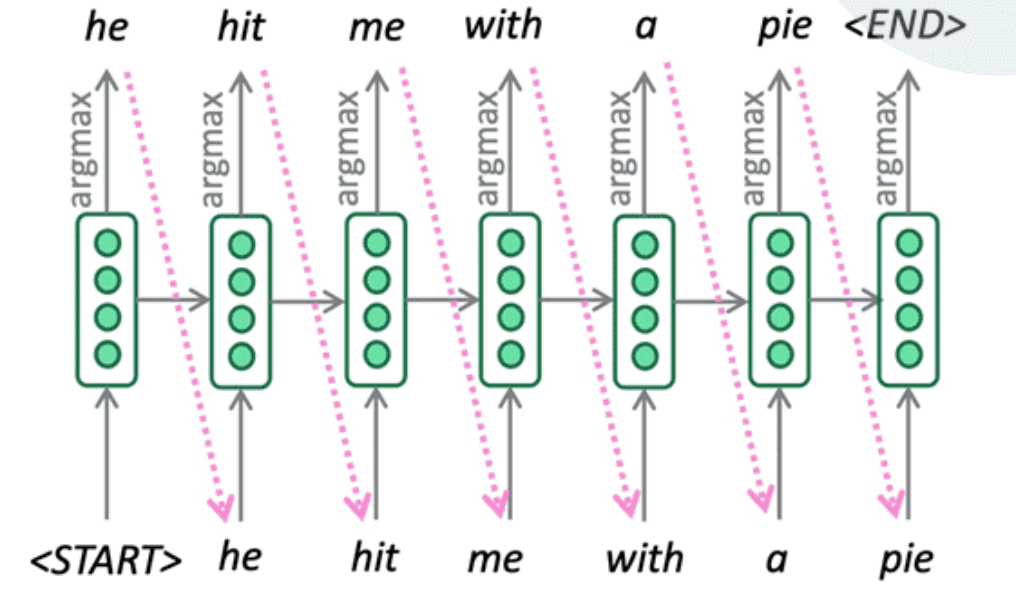
全局搜索(Exhaustive Search)
众所周知,贪心思想往往找不到全局最优解,只能得到局部最优解。所以另一种极端的做法就是全局搜索。叫穷举搜索也可以,笔者喜欢叫全局搜索。每次都选择所有的单词。
如果词表大小为M,序列长度为N,全局搜索将计算所有的序列共 种情况,然后选择概率最大的序列。
集束搜索(Beam Search)
众所周知,穷举思想往往能找到全局最优解,但是性能过差,实用性上还不如贪心思想。而通常这种情况下,都会出现一种折中方案。
集束搜索就是这样一种折中方案。它并不是每一步找最大的一个,也不是找所有,而是**跟踪 _K_ 个最可能的部分序列** ,_K _是集束搜索的参数,成为束宽(beam size)。beam search通过 _K_ 扩大了搜索空间,相比greed search更容易找到全局最优解,相比贪心搜索更快,复杂度从降低到。
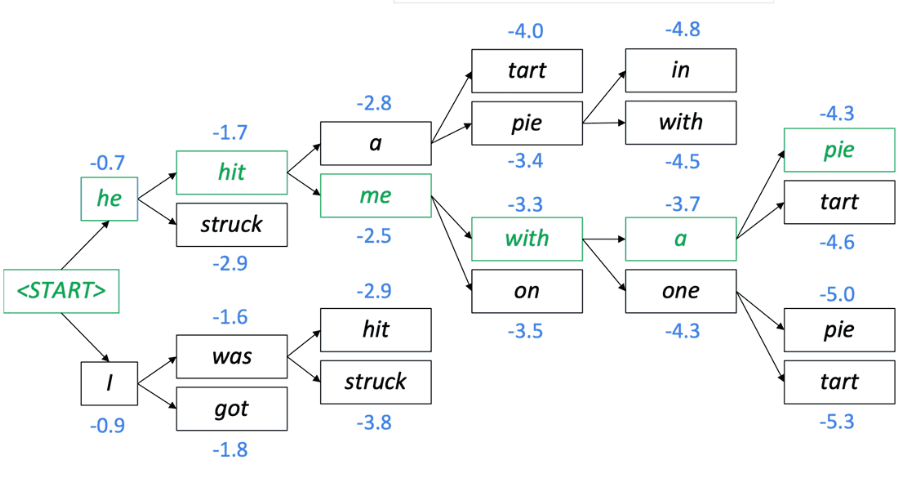
值得注意的是,beam search是每一步选择后保留最大的K个选择,并不是选择前选最大的K 个。因此复杂度是而不是
。Beam Search不保证全局最优,但是比Greedy Search搜索空间更大,一般结果比Greedy Search要好。Greedy search可以看做是 beam size = 1时的 Beam Search。
苏神对 beam search 的理解
苏剑林. (Sep. 01, 2018). 《玩转Keras之seq2seq自动生成标题 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/5861

基于采样的解码
苏剑林. (Jun. 16, 2020). 《如何应对Seq2Seq中的“根本停不下来”问题? 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/7500
对于Seq2Seq来说,我们很多时候希望得到确定性的结果,所以多数场景下我们都是用Beam Search。但是Beam Searc的生成结果可能会出现过于单一的现象(即类似“好的”、“不知道”、“谢谢”这类比较“安全”的回复),或者有时候我们希望增加输出的多样性,这时候就需要随机性解码算法!
解码算法大致可以分为两类:
- 确定性解码算法,就是当输入文本固定之后,解码出来的输出文本也是固定的,这类算法包含贪心搜索(Greedy Search)和束搜索(Beam Search);
- 随机性解码算法,顾名思义,就是哪怕输入文本固定了,解码出来的输出文本也不是固定的,比如从训练语言模型进行随机采样就是这种算法(参考《现在可以用Keras玩中文GPT2了》)。它包含三种情况:原生随机解码、top-k随机解码、Nucleus随机解码。
Softmax Temperature
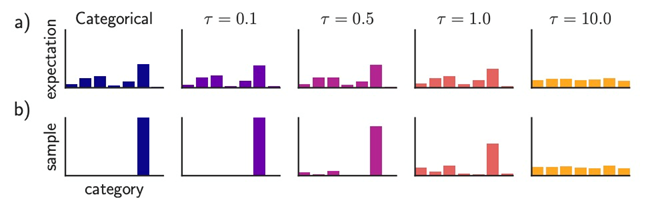
对于文本生成中出现不太连贯和通顺,产生语无伦次的胡言乱语的情况,可以采用带温度参数的Softmax,温度Softmax,可以将Softmax后的概率进行平滑处理,公式如下:
代表了Softmax的一个平滑的程度,
- 当
时,概率分布
趋向于One-hot分布,变得更尖锐;
- 因此输出的多样性较少 (概率集中在顶层词汇上)
- 当
时,概率分布
趋向于均匀分布
- 因此输出更多样化 (概率分布在词汇中)
原生随机采样
原生随机解码很简单,在每个步骤,从概率分布
中随机采样一个token(而不是argmax取概率最大的词)。比如第一步算
,然后按概率随机采样一个token,比如c;然后第二步算
,接着按概率随机采样一个token,比如a;那么第三步就算
,再按概率随机采样;…;依此类推,直到采样到
相比于按概率“掐尖”,这样会增大所选词的范围,引入更多的随机性。
Top-K采样
Top-K Sampling在“得分高”和“多样性”方面做一个折中。 GPT-2就是采用了这种采样方案,这也是其生成故事效果不错的原因之一。
Top-K Sampling的原理是:
- 在每个步骤
,从概率分布
的前
个最可能的单词中,进行随机采样
- 与纯采样类似,但截断概率分布,然后重新归一化概率后再采样
- 此时,
是贪婪搜索,
是纯采样
- 增加
以获得更多样化 / 风险的输出
- 减少
以获得更通用 / 安全的输出
但是在使用Top-K采样时需要注意的一个问题是,它固定了下一次采样的样本集的大小,不会动态适应从下一个单词概率分布。这可能会导致某些单词可能是从非常尖锐的分布中采样的,而另一些单词则是从更平坦的分布中采样的。这可能会使得模型产生乱序的尖峰分布,并限制模型用于平坦分布的创造力。
1、预测下一个字的出现概率next_proba = model.predict(inputs, output_ids, ...)2、保留其中最高的topk概率,并重新归一化k_indices = probas.argpartition(-topk,axis=1)[:, -topk:] # 仅保留topkprobas = np.take_along_axis(probas, k_indices, axis=1) # topk概率probas /= probas.sum(axis=1, keepdims=True) # 重新归一化3、按照概率大小进行随机采样一个4、取出该概率索引对应的字 id,加到 token_ids后面output_ids = np.concatenate([output_ids, sample_ids], 1)5、判断是否为结束标记是:保存生成序列否:循环上述的步骤
Top-p采样 / Nucleus Sampling
Nucleus Sampling也叫Top-p Sampling,这个方法固定候选集合的概率密度和在整个概率分布中的比例,也就是构造一个最小候选集 V,使得候选集 V 的概率和大于设定的阈值 p,即:
然后,将选出来的候选集 V 重新归一化集合内词的概率,并把集合外词的概率设为0。这样,单词集合的大小(也就是集合中单词的数量)可以根据下一个单词的概率分布动态地增加或减少。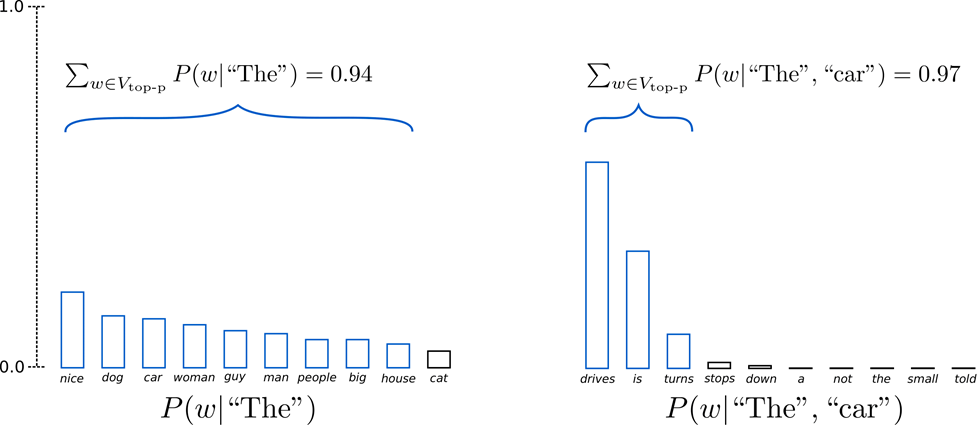
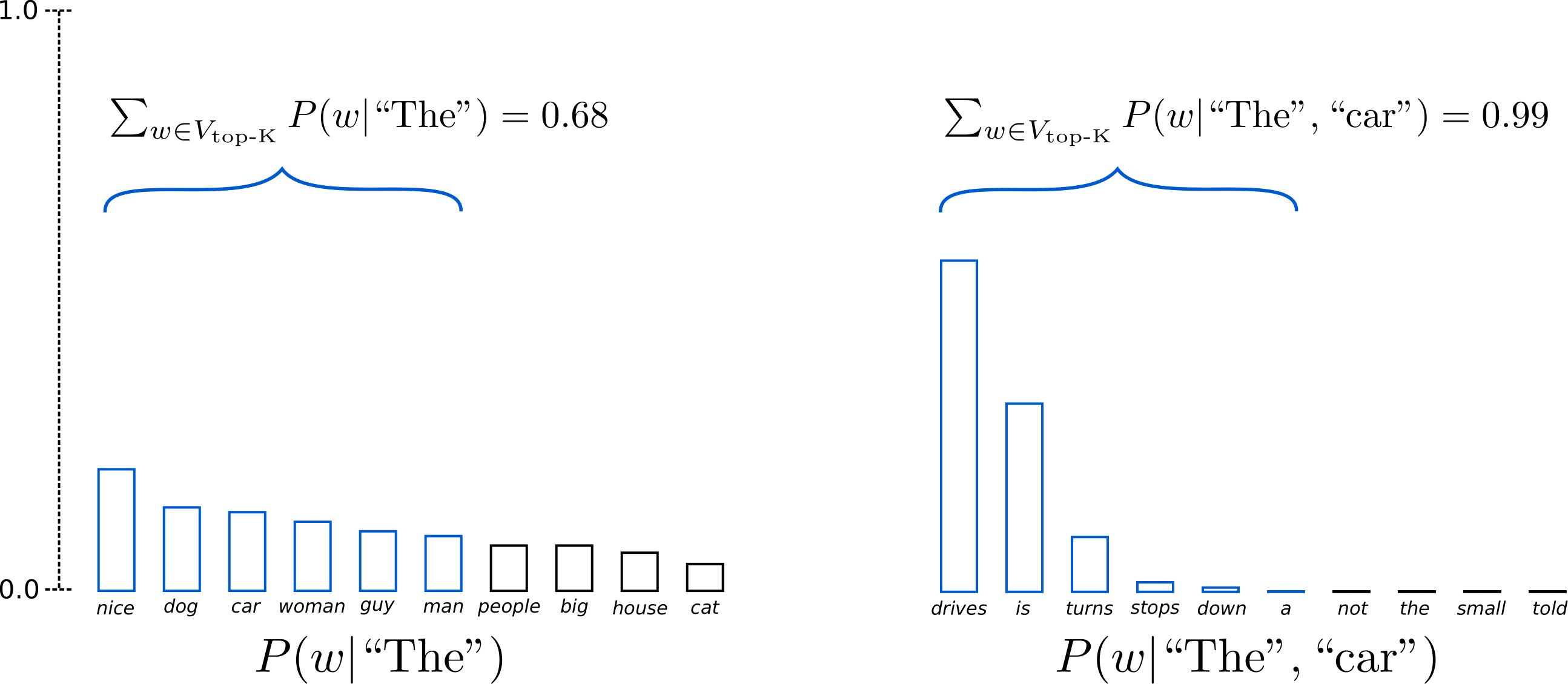
若上图示例设置,定义候选集
为所有单词累计概率超过0.92的最小单词子集。 在第一步采样中,包括了9个最有可能的单词,而在第二步采样中,只需选择前3个单词即可超过92%。这种方法可以使得模型,在当下一个单词的可预测性不确定时,保留较多的单词,例如
;而当下一个单词看起来比较可预测时,只保留几个单词,例如
。
1、预测下一个字的出现概率next_proba = model.predict(inputs, output_ids, ...)2、保留其中最高的topk概率,并重新归一化k_indices = probas.argpartition(-topk,axis=1)[:, -topk:]probas = np.take_along_axis(probas, k_indices, axis=1)probas /= probas.sum(axis=1, keepdims=True)3、构造一个最小候选概率集V,使得V的概率和大于设定的阈值 p,并重新归一化cumsum_probas = np.cumsum(probas, axis=1) # 累积概率flag = np.roll(cumsum_probas >= topp, 1, axis=1) # 标记超过topp的部分flag[:, 0] = False # 结合上面的np.roll,实现平移一位的效果probas[flag] = 0 # 后面的全部置零probas /= probas.sum(axis=1, keepdims=True) # 重新归一化4、按照概率大小进行随机采样一个5、取出该概率索引对应的字 id,加到 token_ids后面output_ids = np.concatenate([output_ids, sample_ids], 1)6、判断是否为结束标记是:保存生成序列否:循环上述的步骤
Beam Search 算法细节详解
Beam Search的使用,往往可以得到比Greedy Search更好的结果,道理很容易理解,高手下棋想三步,深思熟虑才能走得远。

beam search的逻辑比较简单,假设beam size为,字典大小为
,满足
,伪代码如上所示。对于某个step t,我们首先对当前活跃的
个节点做拓展产生
个后续节点,具体做法是:先拿到每个节点的
个概率值(总计
个),再对保留每个节点的
得到
个后续节点。随后对此处
个节点取全局的
个节点作为u+1步的活跃节点。
初始条件
u=0的时候采用
终止条件
beam search进行的过程中,当某个活跃节点上产生节点和选取
个节点可以用一次计算完成!
beam size
当beam size较小时,Beam Search会有跟Greedy search类似的问题(Ungrammatical、unnatural、nonsensical、incorrect),当beam size = 1时,Beam Search退化成Greedy search。增大beam size之后,可以解决上面出现的一些问题。但是,更大的beam size会花费更多的计算量,并且会引入一些其他问题。当beam size过高,在翻译任务中会降低BLEU score,因为过高的beam size会导致生成的句子都比较短;在闲聊对话任务中,过高的beam size会让输出过于普通(即无法给人惊喜)。
Beam Search 代码实现
1、随机初始化概率
import numpy as npimport heapq'''概率初始化'''#第一步,每个单词的概率prob_1 = np.random.dirichlet(np.ones(3))#第二步,每种情况下每个单词的概率prob_2 = np.random.dirichlet(np.ones(3),size=3)#第三步,每种情况下每个单词的概率prob_3 = np.random.dirichlet(np.ones(3),size=[3,3])print("prob_1:\n ", prob_1, "\n")print("prob_2:\n ", prob_2, "\n")print("prob_3:\n ", prob_3, "\n")
2、贪婪搜索示例
decode_dict={0:'a',1:'b',2:'c'}def greedy_search_decoder(prob_1,prob_2,prob_3,decode_dict):result=[]key1 = argmax(prob_1)print("解码向量为",prob_1,",所以选",decode_dict[key1])result.append(decode_dict[key1])key2 = argmax(prob_2[key1])print("已经选了",decode_dict[key1],",此时解码向量为",prob_2[key1],",所以选",decode_dict[key2])result.append(decode_dict[key2])key3 = argmax(prob_3[key1][key2])print("已经选了",decode_dict[key1],decode_dict[key2],",此时解码向量为",prob_3[key1][key2],",所以选",decode_dict[key3])result.append(decode_dict[key3])result_str = "最终的选择:"result_str = decode_dict[key1] + "_" + decode_dict[key2] + "_" + decode_dict[key3]print(result_str)return resultprint("\ngreedy_search_decoder:")greedy_search_decoder(prob_1,prob_2,prob_3,decode_dict)
3、集束搜索示例
decode_dict={0:'a',1:'b',2:'c'}# beam searchdef beam_search_decoder(prob_1,prob_2,prob_3,decode_dict, k=2):step = 1prev_all_candidate = heapq.nlargest(k, range(len(prob_1)), prob_1.__getitem__)print("step",step,":")print("解码向量为",prob_1,",候选",[decode_dict[i] for i in prev_all_candidate])print("#######")result_str = "最终的选择:"for i in prev_all_candidate:result_str = result_str + decode_dict[int(i)] + '_'result_str = result_str.strip('_') + ','print(result_str.strip(','))print("#######")step = step + 1prob_dict = {}print("step",step,":")for item in prev_all_candidate:next_all_candidate = heapq.nlargest(k, range(len(prob_2[item])), prob_2[item].__getitem__)print("选择",decode_dict[item],"解码向量为",prob_2[item])for raw in next_all_candidate:prob_dict[str(item)+'_'+str(raw)] = prob_1[item] * prob_2[item][raw]print("候选",decode_dict[raw],"候选概率为",prob_dict[str(item)+'_'+str(raw)])print("#######")order_dict = sorted(prob_dict.items(), key=lambda d:d[1], reverse=True)final_candidate = [ i[0] for i in order_dict[0:k]]result_str = "最终的选择:"for i in final_candidate:for j in i.split('_'):result_str = result_str + decode_dict[int(j)] + '_'result_str = result_str.strip('_') + ','print(result_str.strip(','))print("#######")step = step + 1prob_dict = {}print("step",step,":")prev_all_candidate = final_candidatefor item in prev_all_candidate:item1, item2 = item.split("_")item1 = int(item1)item2 = int(item2)next_all_candidate = heapq.nlargest(k, range(len(prob_3[item1][item2])), prob_3[item1][item2].__getitem__)print("选择",decode_dict[item1],decode_dict[item2],"解码向量为",prob_3[item1][item2])for raw in next_all_candidate:prob_dict[str(item1)+'_'+str(item2)+'_'+str(raw)] = prob_1[item1] * prob_2[item1][item2] * prob_3[item1][item2][raw]print("候选",decode_dict[raw],"候选概率为",prob_dict[str(item1)+'_'+str(item2)+'_'+str(raw)])print("#######")order_dict = sorted(prob_dict.items(), key=lambda d:d[1], reverse=True)final_candidate = [ i[0] for i in order_dict[0:k]]result_str = "最终的选择:"for i in final_candidate:for j in i.split('_'):result_str = result_str + decode_dict[int(j)] + '_'result_str = result_str.strip('_') + ','print(result_str.strip(','))print("\nbeam_search_decoder:")beam_search_decoder(prob_1,prob_2,prob_3,decode_dict, k=2)
4、 集束搜索(苏神实现)
def gen_sent(s, topk=3, maxlen=64):"""beam search解码每次只保留topk个最优候选结果;如果topk=1,那么就是贪心搜索"""xid = np.array([str2id(s)] * topk) # 输入转idyid = np.array([[2]] * topk) # 解码均以<start>开头,这里<start>的id为2scores = [0] * topk # 候选答案分数for i in range(maxlen): # 强制要求输出不超过maxlen字proba = model.predict([xid, yid])[:, i, 3:] # 直接忽略<padding>、<unk>、<start>log_proba = np.log(proba + 1e-6) # 取对数,方便计算arg_topk = log_proba.argsort(axis=1)[:,-topk:] # 每一项选出topk_yid = [] # 暂存的候选目标序列_scores = [] # 暂存的候选目标序列得分if i == 0:for j in range(topk):_yid.append(list(yid[j]) + [arg_topk[0][j]+3])_scores.append(scores[j] + log_proba[0][arg_topk[0][j]])else:for j in range(topk):for k in range(topk): # 遍历topk*topk的组合_yid.append(list(yid[j]) + [arg_topk[j][k]+3])_scores.append(scores[j] + log_proba[j][arg_topk[j][k]])_arg_topk = np.argsort(_scores)[-topk:] # 从中选出新的topk_yid = [_yid[k] for k in _arg_topk]_scores = [_scores[k] for k in _arg_topk]yid = np.array(_yid)scores = np.array(_scores)best_one = np.argmax(scores)if yid[best_one][-1] == 3:return id2str(yid[best_one])# 如果maxlen字都找不到<end>,直接返回return id2str(yid[np.argmax(scores)])
PS:Keras 版本 beam search 可以参考苏神写的通用自回归生成模型解码基类 bert4keras.snippets.AutoRegressiveDecoder()
Beam Search 的问题
Penalize longer sequence
当计算序列可能在文本中出现的概率时,越长的序列会使得概率越小(如下公式),会导致较短的句子更容易被选出。因为score函数的每一项都是负的,序列越长,score往往就越小。
为了解决对长句子惩罚的问题,可以对序列的概率进行归一化,让不同长度的序列有个标准化的概率:
或者使用跟序列长度相关的归一化方法,如下公式:
根据调整后的结果来选择best one。
Repetitive Problem
Beam search在做文本生成的时候,当生成的文本较长时,通常都会出现生成的文本重复的问题,这也是文本生成中一个较为常见的问题。
有研究发现,当文章不断重复的时候,可以让Loss不停地下降,所以导致的文本生成中出现重复。
- 最简单和常用的解决文本生成重复问题的方法,是设置不重复使用n-grams。如果发现生成的是重复的,那就抛弃。这种方法简单且通常比较有用。
- 第二种方法是,在Loss中加一个与文本相似度相关的惩罚项,如下公式:
当生成文本与前文相似度较高时,会使得序列预测的概率更低,生成的Loss变大,从而解决重复问题。
- 第三种方法是使用Unlikelihood Objective方法。它的思想是,生成一个不想要的token的集合,使得每次生成文本的时候,生成集合里的token的概率会被降低。略….
Generic Problem
在人说话的时候是会有一些概率表达的波动的,每个词说出来并不一定是概率最高的,而是偶尔会给人惊喜的词。Beam Search总会选择概率较大的来输出,不太符合人说话时的概率波动。而且在文本生成任务中,它容易会生成出空洞、重复、前后矛盾的文本。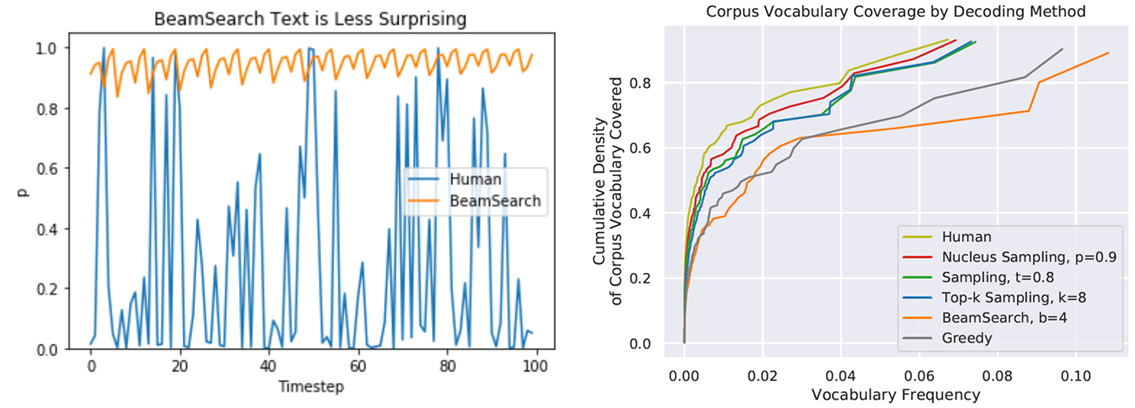
从上图中右边的图看,Sampling的解码方式更符合人们说话的情况。因此,在文本生成任务中Sampling的解码方式更合适。
| 任务类型 | 适用解码 | 应用实例 |
|---|---|---|
| 高熵任务 | Sampling | 文本/对话生成 |
| 低熵任务 | Beam Search | 机器翻译 |
解码算法:总结

- 贪心解码是一种简单的译码方法;给低质量输出
- Beam搜索(特别是高beam大小) 搜索高概率输出
- 比贪婪提供更好的质量,但是如果 Beam 尺寸太大,可能会返回高概率但不合适的输出(如通用的或是短的)
- 采样方法来获得更多的多样性和随机性
- 适合开放式/创意代 (诗歌,故事)
个抽样允许控制多样性
- Softmax 温度控制的另一种方式多样性
- 它不是一个解码算法!这种技术可以应用在任何解码算法。
参考
解码算法系列之集束搜索(Beam Search)
Beam Search快速理解及代码解析(下)
玩转Keras之seq2seq自动生成标题-苏剑林
如何应对Seq2Seq中的“根本停不下来”问题?
NLG过程的优化-小白也能学好深度学习
斯坦福NLP课程 | 第15讲 - NLP文本生成任务

