
逻辑回归(Logistic Regression)虽然被称为回归,但其实际上是分类模型,并常用于二分类。我们知道,线性回归的模型是求出输出特征向量Y和输入样本矩阵X之间的线性关系系数𝜃,满足。此时我们的Y是连续的,所以是回归模型。如果我们想要Y是离散的话,怎么办呢?一个可以想到的办法是,我们对于这个Y再做一次函数转换,变为
。如果我们令
的值在某个实数区间的时候是类别A,在另一个实数区间的时候是类别B,以此类推,就得到了一个分类模型。如果结果的类别只有两种,那么就是一个二元分类模型了。逻辑回归的出发点就是从这来的。下面我们开始引入二元逻辑回归。
二元逻辑回归模型
二元逻辑回归是利用线性模型加上一个Logistic函数(或者也称为 Sigmoid 函数),将线性模型得到的连续结果映射到离散型上,当 … 大于某个值(通常设为0.5)时,便可以认为样本属于正类,反之则认为属于负类。
如果用 x 表示数据点,用 y表示类别(y可以取1或者-1,代表两个不同的类),一个线性分类器的学习目标便是要在 n 维的数据空间中找到一个决策边界(Decision Boundary)也称 超平面(hyper plane),这个超平面的方程可以表示为:
对线性回归的结果做一个在函数g上的转换,可以变化为逻辑回归。这个函数g在逻辑回归中一般为sigmoid函数,形式如下:
它有一个非常好的性质,即当z趋于正无穷时,趋于1,而当z趋于负无穷时,𝑔(𝑧)趋于0,这非常适合于我们的分类概率模型。另外,它还有一个很好的导数性质:
%20%26%3D%5Cfrac%7Bd%7D%7Bd%20z%7D%20%5Cfrac%7B1%7D%7B1%2Be%5E%7B-z%7D%7D%20%5C%5C%0A%26%3D%5Cfrac%7B1%7D%7B%5Cleft(1%2Be%5E%7B-z%7D%5Cright)%5E%7B2%7D%7D%5Cleft(e%5E%7B-z%7D%5Cright)%20%5C%5C%0A%26%3D%5Cfrac%7B1%7D%7B%5Cleft(1%2Be%5E%7B-z%7D%5Cright)%7D%20%5Ccdot%5Cleft(1-%5Cfrac%7B1%7D%7B%5Cleft(1%2Be%5E%7B-z%7D%5Cright)%7D%5Cright)%20%5C%5C%0A%26%3Dg(z)(1-g(z))%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0Ag%5E%7B%5Cprime%7D%28z%29%20%26%3D%5Cfrac%7Bd%7D%7Bd%20z%7D%20%5Cfrac%7B1%7D%7B1%2Be%5E%7B-z%7D%7D%20%5C%5C%0A%26%3D%5Cfrac%7B1%7D%7B%5Cleft%281%2Be%5E%7B-z%7D%5Cright%29%5E%7B2%7D%7D%5Cleft%28e%5E%7B-z%7D%5Cright%29%20%5C%5C%0A%26%3D%5Cfrac%7B1%7D%7B%5Cleft%281%2Be%5E%7B-z%7D%5Cright%29%7D%20%5Ccdot%5Cleft%281-%5Cfrac%7B1%7D%7B%5Cleft%281%2Be%5E%7B-z%7D%5Cright%29%7D%5Cright%29%20%5C%5C%0A%26%3Dg%28z%29%281-g%28z%29%29%0A%5Cend%7Baligned%7D%0A&id=qziEV)
如果我们令中的z为:
,这样就得到了二元逻辑回归模型的一般形式:
理解了二元分类回归的模型,接着我们就要看模型的损失函数了,我们的目标是极小化损失函数来得到对应的模型系数𝜃。
二元逻辑回归的损失函数
回顾下线性回归的损失函数,由于线性回归是连续的,所以可以使用模型误差的的平方和来定义损失函数。但是逻辑回归不是连续的,自然线性回归损失函数定义的经验就用不上了。不过我们可以用最大似然估计来推导出我们的损失函数。
我们知道,按照第二节二元逻辑回归的定义,假设我们的样本输出是0或者1两类。那么我们有:
把这两个式子写成一个式子,就是:
其中y的取值只能是0或者1。
得到了y的概率分布函数表达式,我们就可以用似然函数最大化来求解我们需要的模型系数𝜃。为了方便求解,这里我们用对数似然函数最大化,对数似然函数取反即为我们的损失函数。似然函数的代数表达式为:
%20%26%3Dp(%5Cvec%7By%7D%20%5Cmid%20X%20%3B%20%5Ctheta)%20%5C%5C%0A%26%3D%5Cprod%7Bi%3D1%7D%5E%7Bm%7D%20p%5Cleft(y%5E%7B(i)%7D%20%5Cmid%20x%5E%7B(i)%7D%20%3B%20%5Ctheta%5Cright)%20%5C%5C%0A%26%3D%5Cprod%7Bi%3D1%7D%5E%7Bm%7D%5Cleft(h%7B%5Ctheta%7D%5Cleft(x%5E%7B(i)%7D%5Cright)%5Cright)%5E%7By%5E%7B(i)%7D%7D%5Cleft(1-h%7B%5Ctheta%7D%5Cleft(x%5E%7B(i)%7D%5Cright)%5Cright)%5E%7B1-y%5E%7B(i)%7D%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AL%28%5Ctheta%29%20%26%3Dp%28%5Cvec%7By%7D%20%5Cmid%20X%20%3B%20%5Ctheta%29%20%5C%5C%0A%26%3D%5Cprod%7Bi%3D1%7D%5E%7Bm%7D%20p%5Cleft%28y%5E%7B%28i%29%7D%20%5Cmid%20x%5E%7B%28i%29%7D%20%3B%20%5Ctheta%5Cright%29%20%5C%5C%0A%26%3D%5Cprod%7Bi%3D1%7D%5E%7Bm%7D%5Cleft%28h%7B%5Ctheta%7D%5Cleft%28x%5E%7B%28i%29%7D%5Cright%29%5Cright%29%5E%7By%5E%7B%28i%29%7D%7D%5Cleft%281-h%7B%5Ctheta%7D%5Cleft%28x%5E%7B%28i%29%7D%5Cright%29%5Cright%29%5E%7B1-y%5E%7B%28i%29%7D%7D%0A%5Cend%7Baligned%7D%0A&id=ZeQ7C)
其中m为样本的个数。
对似然函数对数化取反的表达式,即损失函数表达式为:
逻辑回归也会面临过拟合问题,所以我们也要考虑正则化。所以,
- 二元逻辑回归的L1正则化损失函数表达式如下:
- 二元逻辑回归的L2正则化损失函数表达式如下:
二元逻辑回归 Loss 图解
https://towardsdatascience.com/logistic-regression-detailed-overview-46c4da4303bc
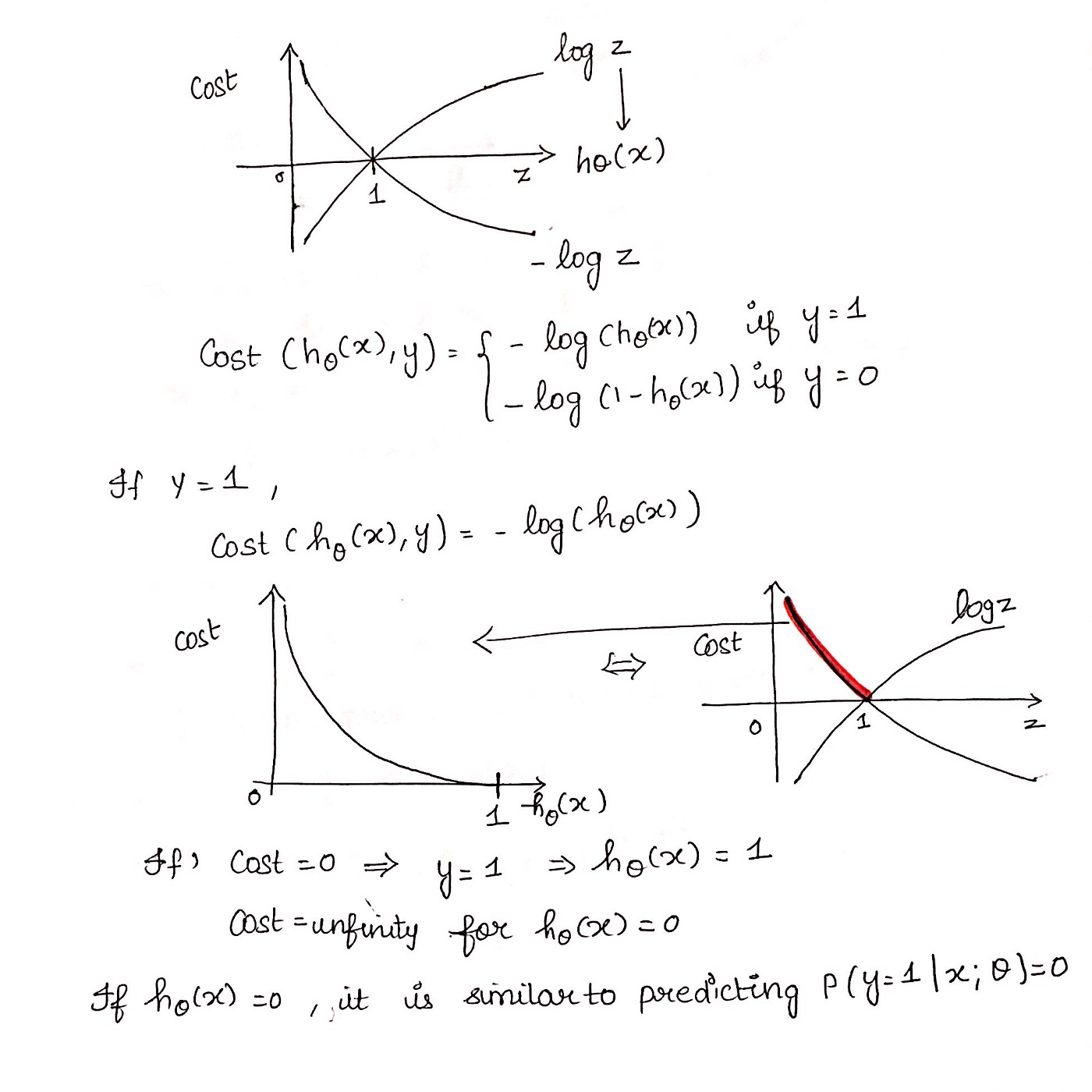
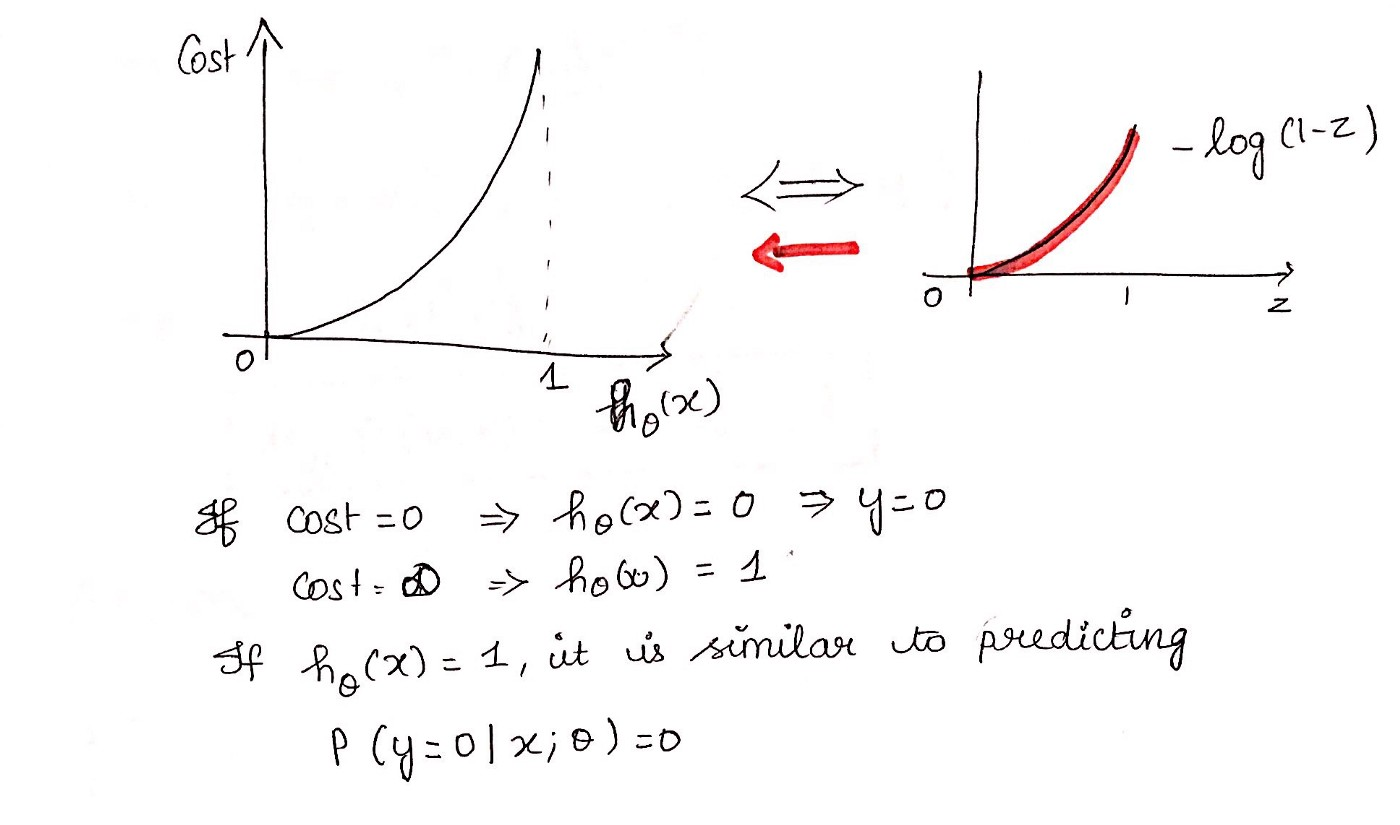
推导梯度下降算法的公式
https://towardsdatascience.com/logistic-regression-detailed-overview-46c4da4303bc

图 11:梯度下降算法第 1 部分
图 12:梯度下降第 2 部分
二元逻辑回归的推广:多元逻辑回归
当然,Logistic Regression也可以用于处理多分类问题,即所谓的“多分类逻辑回归”(Multiclass Logistic Regression)。在单标签多分类任务下,使用多项逻辑回归(Softmax Regression)来进行分类
%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7D%0Ap(y%3D1%20%5Cmid%20x%20%3B%20%5Ctheta)%20%5C%5C%0Ap(y%3D2%20%5Cmid%20x%20%3B%20%5Ctheta)%20%5C%5C%0A%5Cvdots%20%5C%5C%0Ap(y%3Dk%20%5Cmid%20x%20%3B%20%5Ctheta)%0A%5Cend%7Barray%7D%5Cright%5D%3D%5Cfrac%7B1%7D%7B%5Csum%7Bj%3D1%7D%5E%7Bk%7D%20%5Cmathrm%7Be%7D%5E%7B%5Ctheta%7Bj%7D%5E%7B%5Cmathrm%7BT%7D%7D%20x%7D%7D%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7D%0A%5Cmathrm%7Be%7D%5E%7B%5Ctheta%7B1%7D%5E%7B%5Cmathrm%7BT%7D%7D%20x%7D%20%5C%5C%0A%5Cmathrm%7Be%7D%5E%7B%5Ctheta%7B2%7D%5E%7B%5Cmathrm%7BT%7D%7D%20x%7D%20%5C%5C%0A%5Cvdots%20%5C%5C%0A%5Cmathrm%7Be%7D%5E%7B%5Ctheta%7Bk%7D%5E%7B%5Cmathrm%7BT%7D%7D%20x%7D%0A%5Cend%7Barray%7D%5Cright%5D%0A#card=math&code=h%7B%5Ctheta%7D%28x%29%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7D%0Ap%28y%3D1%20%5Cmid%20x%20%3B%20%5Ctheta%29%20%5C%5C%0Ap%28y%3D2%20%5Cmid%20x%20%3B%20%5Ctheta%29%20%5C%5C%0A%5Cvdots%20%5C%5C%0Ap%28y%3Dk%20%5Cmid%20x%20%3B%20%5Ctheta%29%0A%5Cend%7Barray%7D%5Cright%5D%3D%5Cfrac%7B1%7D%7B%5Csum%7Bj%3D1%7D%5E%7Bk%7D%20%5Cmathrm%7Be%7D%5E%7B%5Ctheta%7Bj%7D%5E%7B%5Cmathrm%7BT%7D%7D%20x%7D%7D%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7D%0A%5Cmathrm%7Be%7D%5E%7B%5Ctheta%7B1%7D%5E%7B%5Cmathrm%7BT%7D%7D%20x%7D%20%5C%5C%0A%5Cmathrm%7Be%7D%5E%7B%5Ctheta%7B2%7D%5E%7B%5Cmathrm%7BT%7D%7D%20x%7D%20%5C%5C%0A%5Cvdots%20%5C%5C%0A%5Cmathrm%7Be%7D%5E%7B%5Ctheta_%7Bk%7D%5E%7B%5Cmathrm%7BT%7D%7D%20x%7D%0A%5Cend%7Barray%7D%5Cright%5D%0A&id=FDzAQ)
当存在样本可能属于多个标签的情况时,我们可以训练 k 个二分类的逻辑回归分类器。第 i 个分类器用以区分每个样本是否可以归为第i类,训练该分类器时,需要把标签重新整理为“第i类标签”与“非第i类标签”两类。通过这样的办法,我们就解决每个样本可能拥有多个标签的情况。
小结
逻辑回归尤其是二元逻辑回归是非常常见的模型,训练速度很快,虽然使用起来没有支持向量机(SVM)那么占主流,但是解决普通的分类问题是足够了,训练速度也比起SVM要快不少。如果你要理解机器学习分类算法,那么第一个应该学习的分类算法个人觉得应该是逻辑回归。理解了逻辑回归,其他的分类算法再学习起来应该没有那么难了。

