title: 常见损失函数
subtitle: About loss and loss functions
date: 2021-12-12
author: NSX
catalog: true
tags: Loss
- Loss functions
- Loss functions for regression
- Mean Absolute Error (L1 Loss)
- Mean Squared Error
- Mean Absolute Percentage Error
- Root Mean Squared Error (L2 Loss)
- Logcosh
- Huber loss
- Loss functions for classification
- Hinge
- Squared hinge
- Categorical / multiclass hinge
- Binary crossentropy
- Categorical crossentropy
- Sparse categorical crossentropy
- Kullback-Leibler divergence
- Loss functions for regression
先思考一个问题。损失函数、代价函数和目标函数是一回事吗? 三者之间的关系大概是这样的。
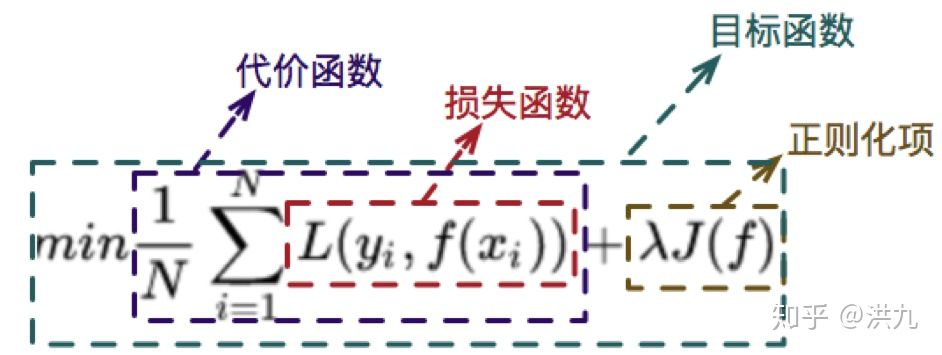
损失函数是一个非负实数函数,用来量化模型预测和真实标签之间的差异。深度学习训练模型的时候就是通过计算损失函数,更新模型参数,从而减小优化误差,直到损失函数值下降到目标值 或者 达到了训练次数。
Loss functions for regression
1.1 Mean Absolute Error (L1 Loss)
平均绝对误差:Mean Absolute Error (MAE):MAE表示了预测值与目标值之间差值的绝对值然后求平均
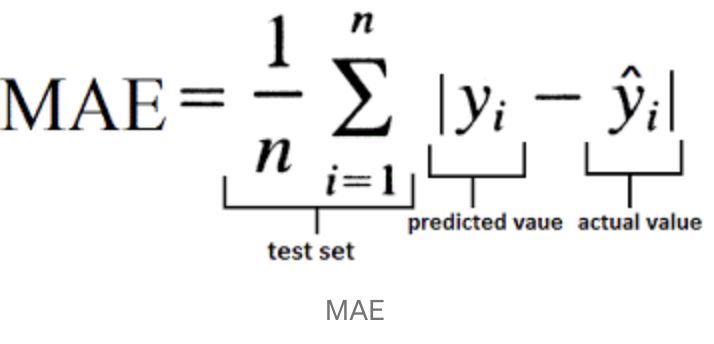
L1 损失具有稀疏性,为了惩罚较大的值,因此常常将其作为正则项添加到其他损失函数中作为约束,L1 损失的最大问题在于梯度在零点不平滑,会导致跳过极小值。
1.2 Mean Squared Error
均方误差 Mean Squared Error (MSE):MSE表示了预测值与目标值之间差值的平方和然后求平均
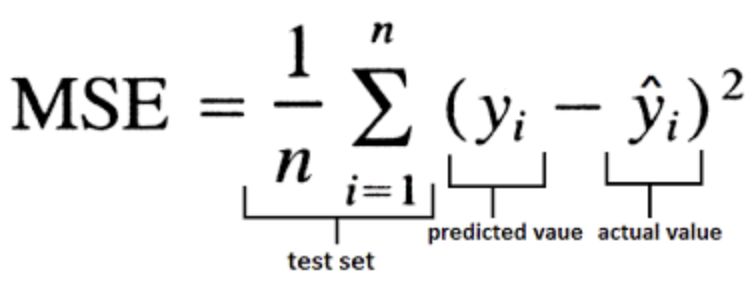
简单直观,易于求导,当预测值与目标值差异很大时,梯度容易爆炸,通常用于回归任务。
但其背后也是有深刻的数学原理的。
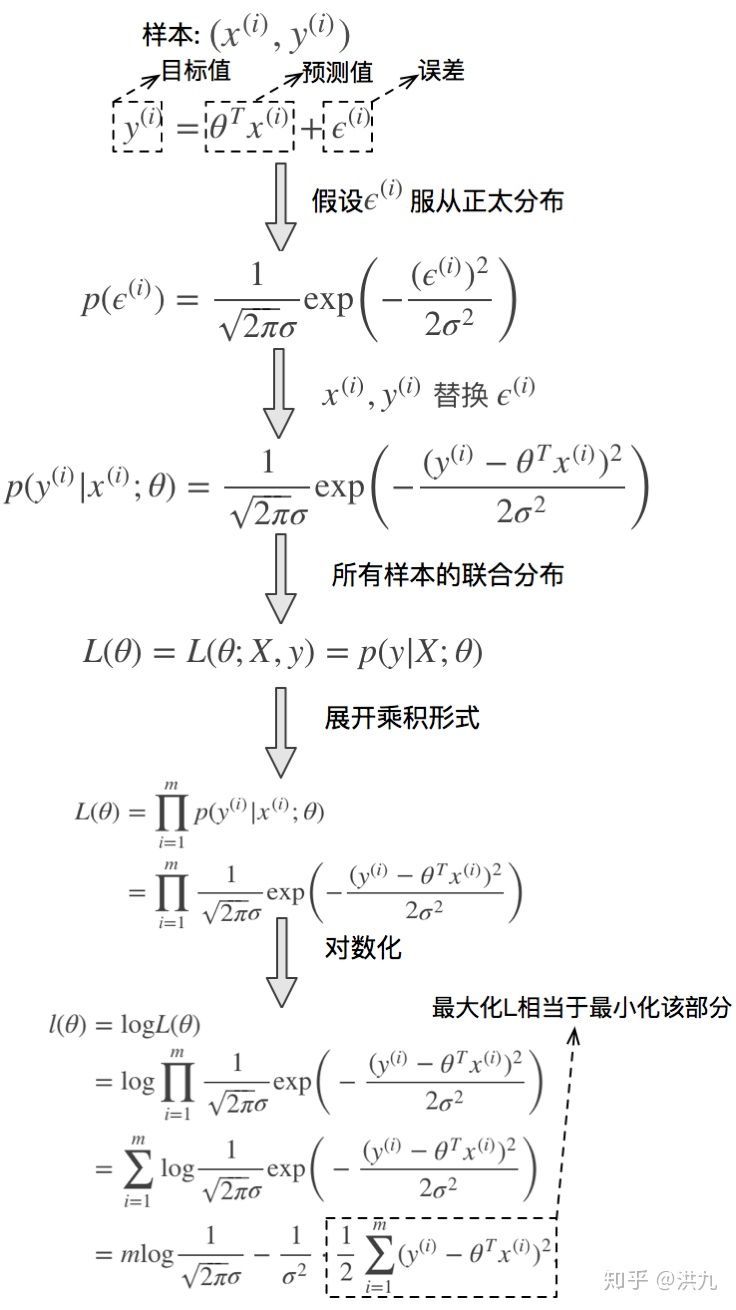
推导过程从最大似然出发,并且在误差服从正太分布的假设下,得出极大化最大似然等价于最小化残差平方和的结论。不过稍微了解下就可以了。
MSE,MAE对比:
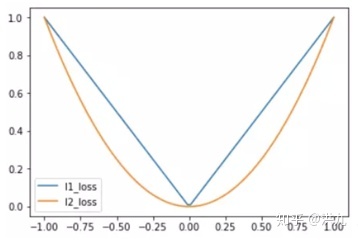
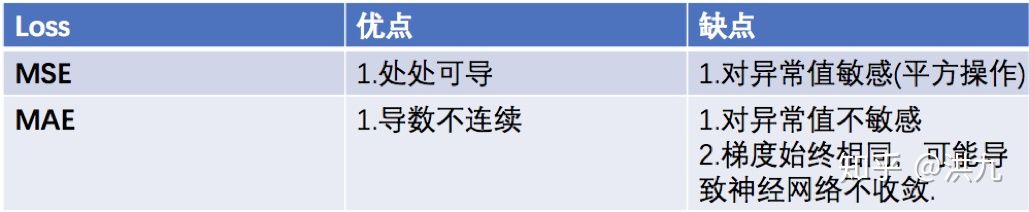
1.3 Root Mean Squared Error (L2 Loss)
均方根误差 Root Mean Squared Error (RMSE)
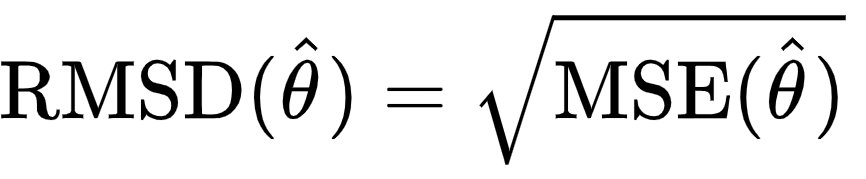
1.4 Huber loss
Huber Loss是一种用于回归问题的有参损失函数,其结合了MSE(处处可导)和MAE(对异常值不敏感)的优点。当预测偏差小于delta时,采用平方误差;当预测偏差大于delta时,采用线性误差。其中delta是需要确定的超参数。Huber Loss定义如下:(目标 t 和预测 p 之间的差异)
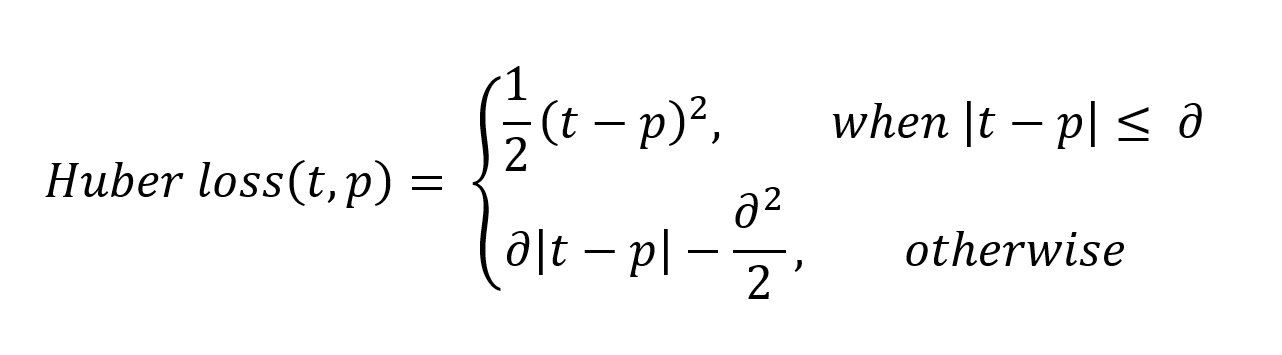
当 𝛿 ~ 0 时 Huber 损失接近 MAE,当𝛿 ~ ∞ 时接近 MSE
Loss functions for classification
2.1 Hinge Loss
铰链损失 Hinge 主要用于支持向量机中,用来解决SVM中的间距最大化问题。它的称呼来源于损失的形状,定义为:
%3D%5Cmax%20(0%2C1-y%20%5Chat%7By%7D)%0A#card=math&code=l%28%5Chat%7By%7D%2C%20y%29%3D%5Cmax%20%280%2C1-y%20%5Chat%7By%7D%29%0A&id=vtyul)
其中 y 的标签为1或-1,是分类器输出的预测值. 如果分类正确,loss为0,否则为
。其含义为,当 Y 和
#card=math&code=f%28x%29&id=is2Jx) 的符号相同时(表示
#card=math&code=f%28x%29&id=RQJCf) 预测正确)并且|
#card=math&code=f%28x%29&id=jsDSe) |≥1时,hinge loss为0;当 Y 和
#card=math&code=f%28x%29&id=UJWdr) 的符号相反时,hinge loss随着
#card=math&code=f%28x%29&id=ZgEtA) 的增大线性增大。也即是,hinge损失不仅会惩罚错误的预测,也会惩罚那些正确预测但是置信度低的样本.
2.2 Categorical / multiclass hinge
hinge loss 仅适用于实际目标值为 +1 或 -1 的二元分类问题,但还有许多其他问题无法以二元方式解决。所以多类 hinge Loss 被提出,其公式如下:
%3D%5Csum%7By%20%5Cneq%20t%7D%20%5Cmax%20%5Cleft(0%2C1%2B%5Cmathbf%7Bw%7D%7By%7D%20%5Cmathbf%7Bx%7D-%5Cmathbf%7Bw%7D%7Bt%7D%20%5Cmathbf%7Bx%7D%5Cright)%0A#card=math&code=%5Cell%28y%29%3D%5Csum%7By%20%5Cneq%20t%7D%20%5Cmax%20%5Cleft%280%2C1%2B%5Cmathbf%7Bw%7D%7By%7D%20%5Cmathbf%7Bx%7D-%5Cmathbf%7Bw%7D%7Bt%7D%20%5Cmathbf%7Bx%7D%5Cright%29%0A&id=q3Y7v)
2.3 Binary crossentropy
我们知道信息熵的定义公式为 。假设有两个概率分布
#card=math&code=p%28x%29&id=qspEz) 和
#card=math&code=q%28x%29&id=fve01),其中
是已知的分布(ground truth),
是未知的分布(预测分布),交叉熵函数则是两个分布的互信息,可以反应两分布的相关程度:
。
二元交叉熵的公式表达如下:
%3D-%5Cleft(y%7Bi%7D%20%5Clog%20%5Chat%7By%7D%7Bi%7D%2B%5Cleft(1-y%7Bi%7D%5Cright)%20%5Clog%20%5Cleft(1-%5Chat%7By%7D%7Bi%7D%5Cright)%5Cright)%0A#card=math&code=BCE%5Cleft%28y%7Bi%7D%2C%20%5Chat%7By%7D%7Bi%7D%5Cright%29%3D-%5Cleft%28y%7Bi%7D%20%5Clog%20%5Chat%7By%7D%7Bi%7D%2B%5Cleft%281-y%7Bi%7D%5Cright%29%20%5Clog%20%5Cleft%281-%5Chat%7By%7D%7Bi%7D%5Cright%29%5Cright%29%0A&id=oyCz8)
Loss的推导过程如下:(从极大似然出发得出二分类交叉熵损失形式)

2.4 Categorical crossentropy
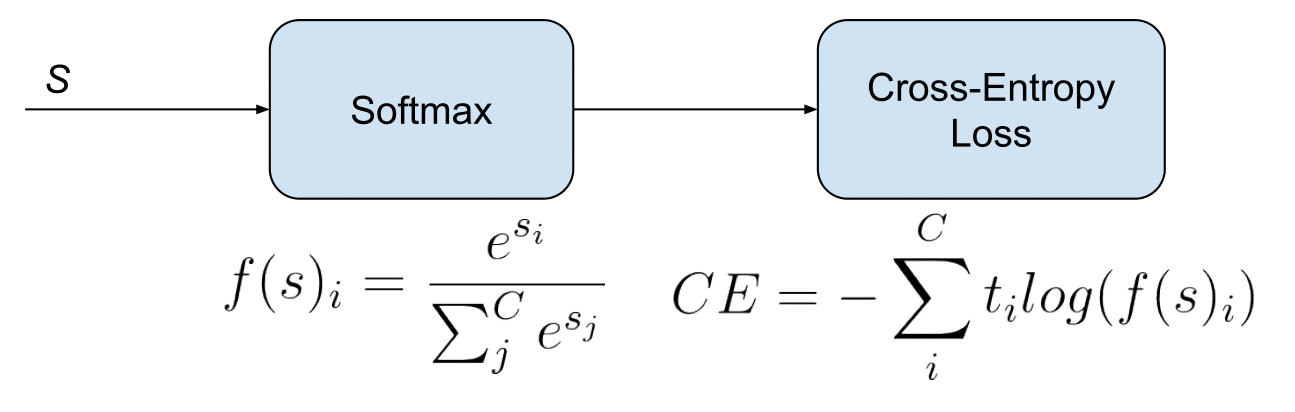
categorical crossentropy (CE) 损失如下:
%3D-%5Csum%7Bi%3D1%7D%5E%7BM%7D%20y%7Bi%7D%20%5Clog%20%5Chat%7By%7D%7Bi%7D%0A#card=math&code=CCE%5Cleft%28y%7Bi%7D%2C%20%5Chat%7By%7D%7Bi%7D%5Cright%29%3D-%5Csum%7Bi%3D1%7D%5E%7BM%7D%20y%7Bi%7D%20%5Clog%20%5Chat%7By%7D%7Bi%7D%0A&id=peTbc)
原始的 softmax 函数非常优雅、简洁,广泛应用于分类问题。**它的特点就是优化类间的距离非常棒,但是优化类内距离时比较弱。Softmax Loss 在 TensorFlow 中的实现可以如下:
# 得到句子表示 ee = tf.reshape(newe_final.stack(), [-1, self.n_hidden])# 将句子表示转换为一个 T 维向量(T 为类别数)self.predict = tf.matmul(e, weights['softmax']) + biases['softmax']# 计算总损失self.total_loss = tf.nn.softmax_cross_entropy_with_logits(logits = self.predict, labels = self.labels))# 计算平均损失self.loss = tf.reduce_mean(self.total_loss)
2.5 Sparse categorical crossentropy
当 label 是整数目标而非分类格式时,可使用Sparse categorical crossentropy!它的执行方式与常规分类交叉熵损失非常相似,但允许您使用整数目标!
2.6 Kullback-Leibler divergence
KL散度用来衡量两个分布之间的相似性,定义公式为:
%3D%5Csum%7Bi%7D%20p%7Bi%7D%20%5Clog%20%5Cleft(%5Cfrac%7Bp%7Bi%7D%7D%7Bq%7Bi%7D%7D%5Cright)%0A#card=math&code=K%20L%28p%20%5Cmid%20q%29%3D%5Csum%7Bi%7D%20p%7Bi%7D%20%5Clog%20%5Cleft%28%5Cfrac%7Bp%7Bi%7D%7D%7Bq%7Bi%7D%7D%5Cright%29%0A&id=v9toV)
KL 散度是非负的,只有当 p 与 q 处处相等时,才会等于0。KL 散度也可以写成:
%3D%5Csum%7Bi%7D%20p%7Bi%7D%20%5Clog%20p%7Bi%7D-p%7Bi%7D%20%5Clog%20q%7Bi%7D%3D-l(p%2C%20p)%2Bl(p%2C%20q)%0A#card=math&code=K%20L%28p%20%5Cmid%20q%29%3D%5Csum%7Bi%7D%20p%7Bi%7D%20%5Clog%20p%7Bi%7D-p%7Bi%7D%20%5Clog%20q%7Bi%7D%3D-l%28p%2C%20p%29%2Bl%28p%2C%20q%29%0A&id=zaCBK)
因此 #card=math&code=KL%28p%7Cq%29&id=nlAEf)的散度也可以说是p与q的交叉熵和p信息熵的和。同时需要注意的时,KL散度对p、q是非对称的。
参考
Retrieval with Deep Learning: A Ranking loss Survey Part 1
Retrieval with Deep Learning: A Ranking-Losses Survey Part 2

