下面我们就来看下深度学习社区为应对深层神经网络的挑战而广泛采用的一些算法。
Momentum
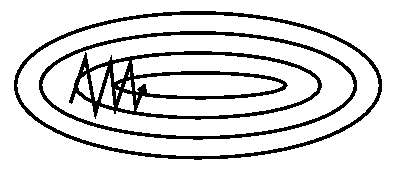
Qian, N. 1999 提出的动量法(Momentum)可以帮助 SGD 在有关方向上加速前进并抑制震荡,如下所示
 |
 |
|---|---|
具体做法是给当前更新向量加上一个比例因子为 γ 的过往更新向量,使得每一次的参数更新方向不仅取决于当前位置的梯度,还受到上一次参数更新方向的影响。优化公式如下: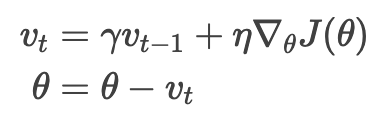

实际上,使用动量的时候我们是推一个球下坡,向下滚的时候小球会积聚动量,滚的越来越快(直到达到终极速度,如果有空气阻力的话,即 γ<1)。参数更新是一回事:梯度指向相同的维度上动量增长,梯度变向的维度上动量减小。结果就是收敛更快,震荡更小。
Nestrov Momentum
但对一个往坡下滚的小球来说,盲目地选择斜坡肯定是很难令人满意。我们希望球能聪明点,对它正要往哪走能有个概念,这样在坡度再次上升之前就能提前减速。
Nesterov, Y. 1983 提出的 Nesterov 梯度加速(NAG)就是这样一种赋予动量项前瞻能力的方法。既然动量方案中我们会用动量来调整参数 θ,所以算下
就能大概知道参数的下一个位置(更新全程不见梯度),粗略了解参数会变成怎样。不用当前参数 θ 计算梯度而是用参数在未来大概率所处的位置来计算,我们就有了很强的预见能力:
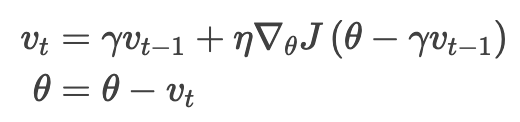
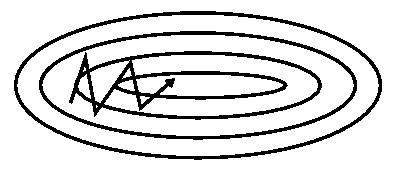
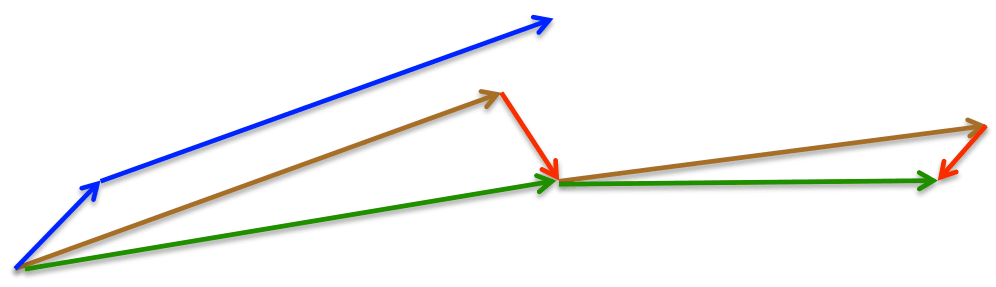
还是一样,将设为 0.9 左右的值。Momentum 方法会先计算当前梯度(图 4 中的小蓝色向量)然后跨一大步迈向更新后的累积梯度方向(大蓝色向量),而 NAG 会先往之前累积梯度的方向迈一大步(棕色向量),算下梯度然后做些修正(红色向量),二者结合实现完整的 NAG 更新(绿色向量)。这种有预见性的更新可以防止我们走得太快,加快了响应速度,Bengio 等人,2012 证实该方法可以显著增强 RNN 在许多任务上的性能。
Adagrad
Duchi 等,2011 提出的 Adagrad 就是一种这么做的基于梯度的优化算法:让学习率适应参数,频繁出现的特征的参数更新幅度小些(即学习率更小),不那么频繁的特征更新幅度大些(即学习率更大)。
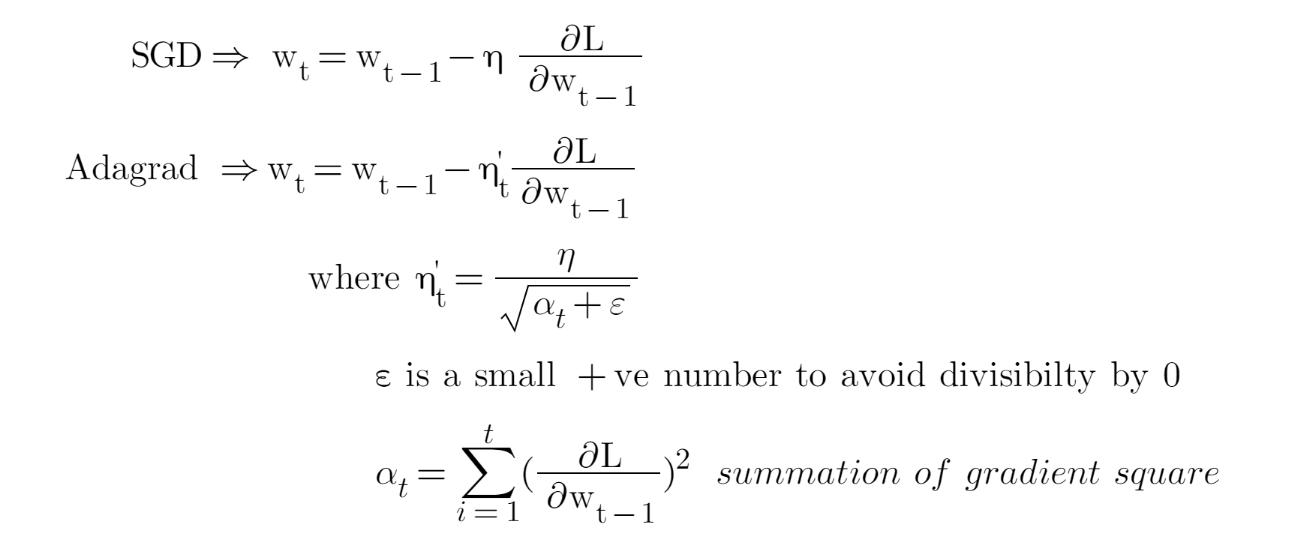

Adagrad 一大优点在于省去了手工调整学习率的麻烦,绝大多数实现都是选了默认值 0.01 后就扔那了。
Adagrad 的主要缺陷出在分母上的梯度平方和:因为加入的每一项都是正的,累加和在训练时一直在增长。这会导致学习率萎缩并最终变得微乎其微,最后可能会导致参数无法更新。下面介绍的算法就要试图解决这一问题。
Adadelta
Zeiler,2012 提出的 Adadelta 是对 Adagrad 的拓展,希望“拯救”一下它那迅速单边减小的学习率。Adadelta 背后的想法是,如果我们可以限制窗口大小,而不是总结过去从 1 到“t”时间步长的所有平方梯度。例如,计算过去 10 个梯度的平方梯度并取平均值。这可以使用梯度上的指数加权平均值来实现。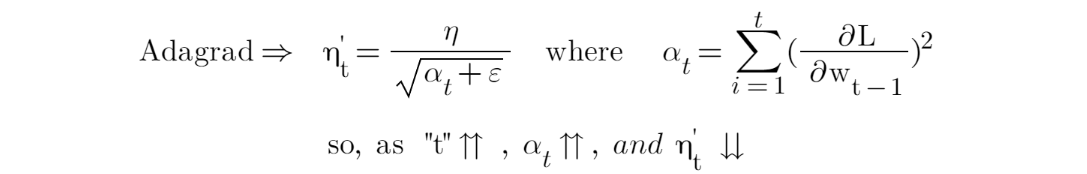
上面的等式表明,随着时间步长“t”的增加,平方梯度的总和“α”增加,这导致学习率“η”降低。为了解决平方梯度“α”总和的指数增长,我们将“α”替换为平方梯度的指数加权平均值。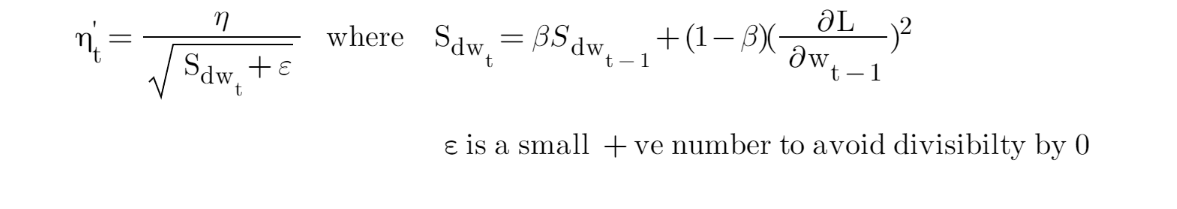
因此,这里与 Adagrad 中的 alpha“α”不同,它在每个时间步后呈指数增长。在 Adadelda,使用过去 Gradient 的指数加权平均值,的增加受到控制。
的计算是利用过往梯度平方的衰减均值。
有了 Adadelta 我们甚至不需要设置默认学习率了,因为它已经从更新式中消失了。
RMSprop
RMSprop 是一个未发表的自适应学习算法,是 Geoff Hinton 在其 Coursera 课程上提出来的。
RMSprop 和 Adadelta 是同一时间分头独立开发的两个技术,都是为了解决 Adagrad 的学习率快速衰减的问题。RMSprop 实际上和我们上面提到的 Adadelta 第一个更新向量一样:
可以看出,Rmsprop与Adagrad类似,只不过cache的计算略微复杂一些,利用了一个衰减因子,这样可以使得
并不是一直处于增大的情况,可以解决Adagrad学习率迅速减小的问题。其中,衰减因子
通常取值为[0.9,0.99,0.999]。
Adam
Kingma 等,2015 提出的自适应矩估计(Adaptive Moment Estimation,Adam)是另一个给每个参数计算自适应学习率的方法。除了像 Adadelta 和 RMSprop 一样存了个指数衰减的过往梯度平方的均值,Adam 还维护了一个指数衰减的过往梯度的均值
,类似于 Momentum。如果将动量法看作是滚球下坡,那 Adam 就是一个有摩擦的重球,也就更偏爱误差表面上平坦的最小值(参见 Heusel 等,2017 )。我们分别按下列式子计算过往梯度和梯度平方的衰减均值:
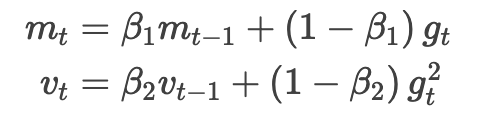
和
分别是梯度的第一矩(均值)和第二矩(有偏方差)的估计值,这也是方法名的由来。因为
和
是被初始化为 0 向量,Adam 作者发现他们会偏向 0,特别是开始时的几步,当学习率衰减的比较小(即
接近于 1)时也尤其明显。于是他们通过求取第一、第二矩估计的偏差修正值来抵消偏差:
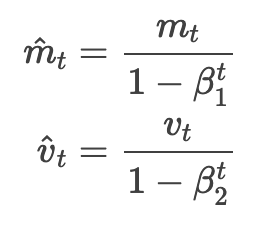
之后就和 Adadelta 与 RMSprop 类似了,把这些用在参数更新上,得到 Adam 更新式:
 |
 |
|---|---|
与Rmsprop类似,Adam除了利用一个衰减因子计算cache以外,还类似Momentum,利用了上一次的参数更新方向,所以可以说Adam是带Momentum的Rmsprop。在参数更新的最初几步中,由于
和
是初始化为0的,为了防止最初几步的更新向0偏差,Adam利用
的 t 次幂来修正这种偏差(t 每次更新加1)。
作者给的默认值为 0.9,
是 0.999,
则是
。作者靠实验证明 Adam 实际表现不错并优于其他自适应学习算法。
NAdam
如前文所见,Adam 可以看作是 RMSprop 和动量法的结合:RMSprop 贡献了指数衰减的过往梯度平方均值 vt,而 Momentum 捐赠了指数衰减的过往梯度均值 mt 。我们也知道了 Nesterov 梯度加速法(NAG)要比一般动量法强。
Dozat,2016 设计的 Nesterov 加速自适应矩估计(Nesterov-accelerated Adaptive Moment Estimation,Nadam)就这样把 Adam 和 NAG 结合在了一起。
RAdam
全名是Rectified Adam,是一種改進Adam的方法,更精確來說,就是自動warmup版的Adam。
AdamW
权重衰减是训练神经网络时用到的一种技术,目的在于保持权重值够小。一般认为大权重会有过拟合的倾向,权重想大理由要充分。衰减技术的实现是通过在损失函数中加一个权重值的函数,这样大权重会显著增大全局损失。最流行的权重衰减形式莫过于 L2 正则化了,它对权重值的平方进行惩罚,能方便的同时处理正、负权重,可微性良好。Ilya 等,2017 设计的 AdamW 修改了 Adam 里权重衰减正则化的传统实现方式,将权重衰减和梯度更新解耦。尤其是,Adam 里 L2 正则化通常是带着下列调整实现的,其中是 t 时步下的权重衰减比率:
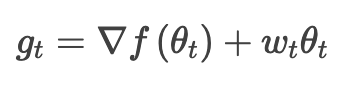
而 AdamW 则转头把权重衰减项挪到了梯度更新式里: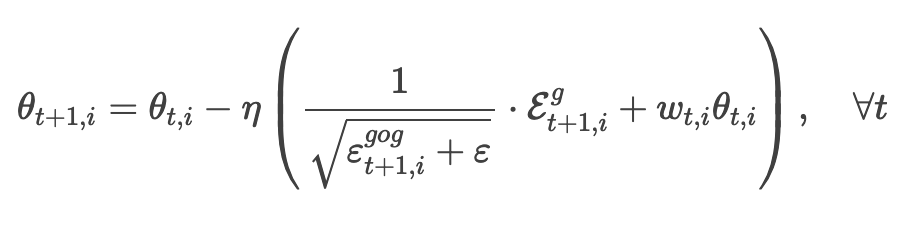
在实践中该方法取得了一定的效果,有被机器学习社区的一些人采纳。就这么一点小改动可以对性能产生那么大的影响,很有趣不是吗?
动态演示
下面是两幅 Alec Radford 绘制的动态图,可以直观感受一下上面多数方法的优化表现。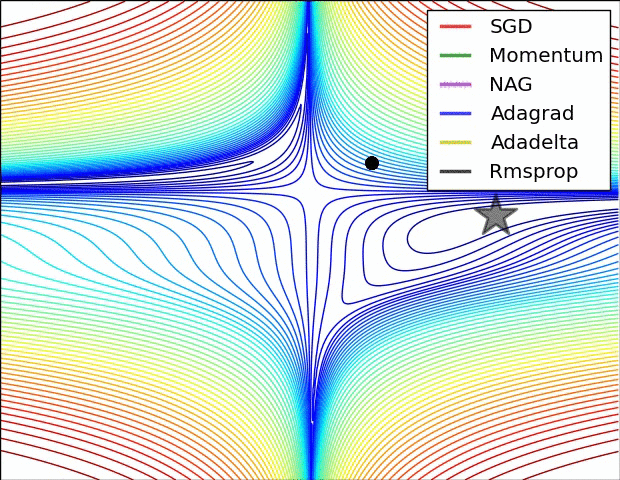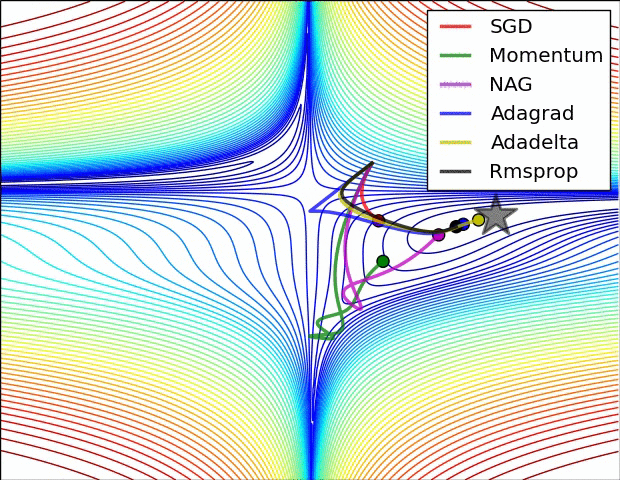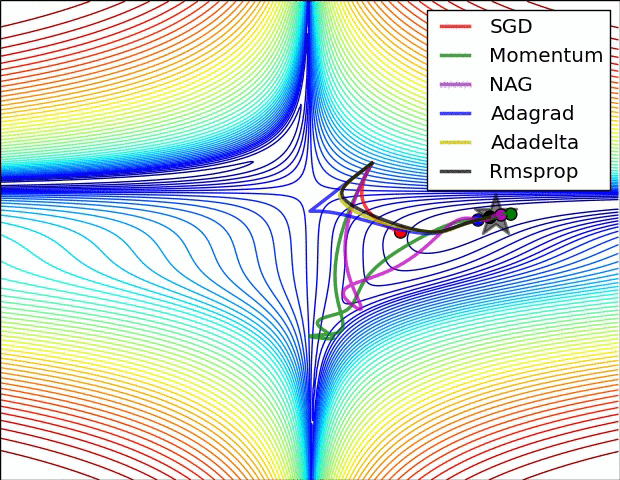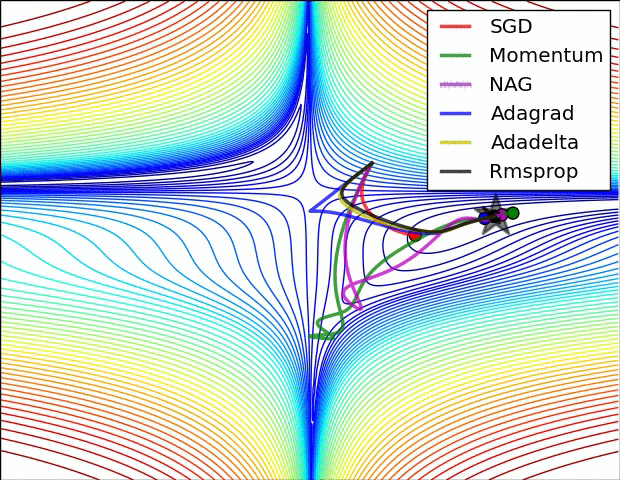
上图显示的是损失表面(Beale 函数)上随时间推移不同方法的行为表现。可以看到 Adagrad,Adadelta 和 RMSprop 几乎是立刻转向正确方向并快速在相似位置收敛,而 Momentum 和 NAG 则偏离了轨道,感觉像是要往坡下滚的球。但由于有前瞻获得的增量反馈, NAG 很快进行了修正并达到最小值。
下面的图 6 则展示了算法在鞍点上的表现,鞍点就是一个维度是正斜率,另一维度是负斜率的点。前文中我们已经说了这对 SGD 是个麻烦,可以看到 SGD,Momentum 和 NAG 很难打破均衡,尽管后两者最终还是设法离开了鞍点。而 Adagrad,RMSprop 和 Adadelta 很快就走向了负斜率。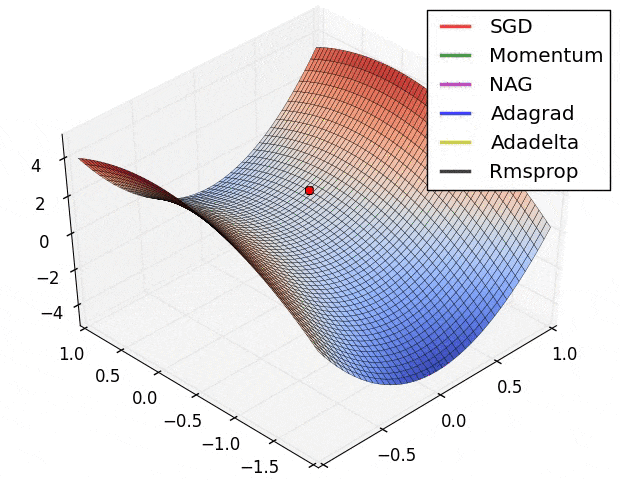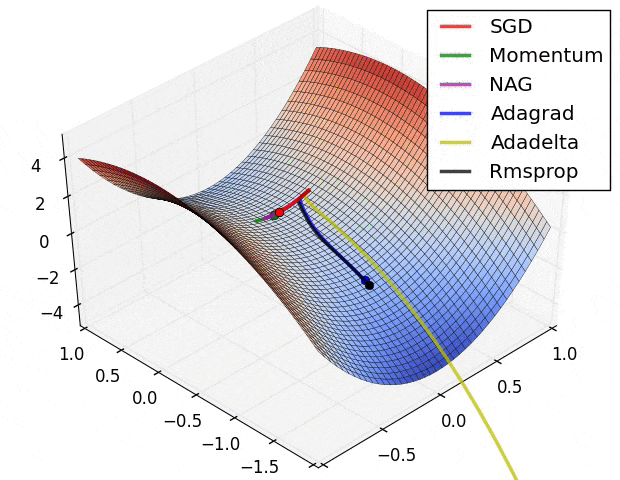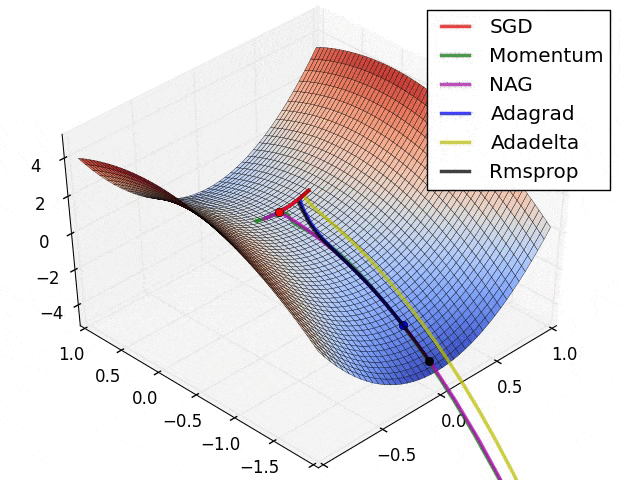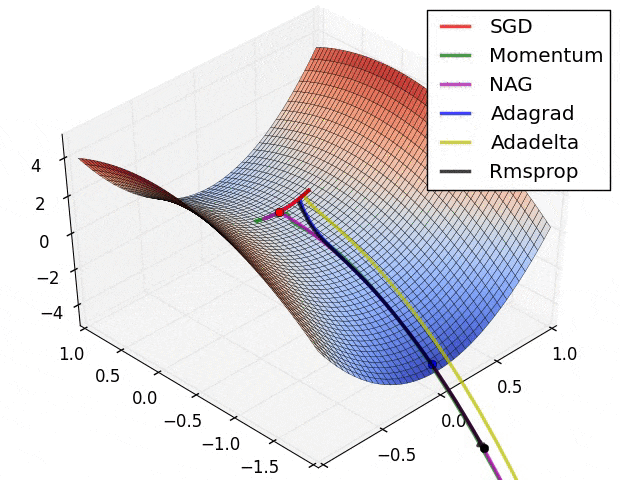
如我们所见,自适应学习率方法,即 Adagrad,Adadelta,RMSprop 和 Adam 是最适合且能得到最佳收敛结果的方法。
选哪个优化器
所以该选哪个优化器呢?如果输入数据稀疏,那选一个自适应学习率方法大概率上效果不会差。这样做的额外一点好处在于不需要调学习率,用默认值就能取得最佳效果。
总的来讲,RMSprop 是对 Adagrad 的扩展,解决了后者学习率快速消失的问题。Adadelta 也一样,只是 Adadelta 是在分子更新中用参数的 RMS 进行更新。最后 Adam 给 RMSprop 加上了动量和偏差修正。所以 RMSprop,Adadelta 和 Adam 在相似环境下差别并不算大。Kingma 等,2015 指出随着梯度变得愈加稀疏,偏差修正能帮 Adam 在抵达优化终点时略胜 RMSprop 一头。

