综合国力 国防 国家安全 国家实力综合指数 硬实力 软实力 标度律 军事装备指数 克莱因综合国力公式

回顾以往计算方式

早期计算公式

  1. **克劳斯·克诺尔**（Klaus Knorr，1956）提出的**国家实力**含义包括**经济能力**，**行政竞争性**和**战争动员能力**。这是最早的综合国力方程，人们已经认识到一个国家的实力不仅仅是经济实力，尽管它是国家实力的基础。
  3. **维·福克斯**（Wilhem Fucks，1965）提出一个**非线性**国力方程。该方程考虑三类变量：一是人口规模（P）；二是能源生产（Z）；三是钢产量（Z<sub>1</sub>）。其方程为：

$ M=(P^2)*Z $

$ M=(P^\frac{3}{2})*Z_1 $

  1. 该方程是以**工业化时代的传统资源**为基础，其主要国家战略目标是全球获取更多的能源，大幅度提高本国的工业生产能力。

克莱因综合国力公式

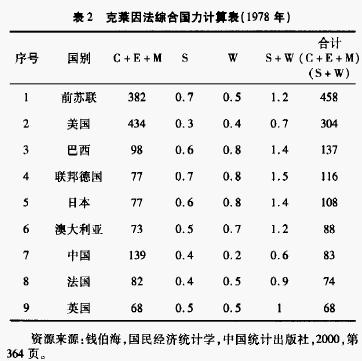
  1. R·S·克莱因(Ray S.Cline)在其书中论述了国际冲突中的国家实力的概念，并在20世纪80年代初对综合国力进行系统的定量比较和分析，认为综合国力分为物质力量和精神力量两部分，这两部分可以相互作用共同促进一国综合国力的提高。测算综合国力的方程为：

$ P_P=(C+E+M)*(S+W)‰ $

  1. P<sub>p</sub>是指现实的国力；C(Critical Mass)为基本实体，包括人口和国土面积；E(Economic Capability)为经济实力；M(Military Capability)为军事实力；S(Strategic Purpose)指战略意图；W(Will to Pursue National Strategy)为国家意志。
  3. 其中，经济实力包括国民生产总值和其他经济指标（能源，工业产能，对外贸易额等）。军事实力包含核力量和常规军力量。

综合国力 - 图1

再定义国力

  1. 受限于冷战思维和时代，以往的国力计算在基础指标（领土，人口等）之外过于注重军事力量，核力量，矿产资源和工业产能。这与我们现在常说的综合国力（Comprehensive National Power， CNP）有很大的不同，<font style="color:#F5222D;">CNP的计算可以根据各种定量指标相结合，建立一个单一的数量来衡量一个民族国家的力量，这些指标考虑采取军事和经济因素（称为硬实力）、文化因素（称为软实力，往往被重点讨论）。</font>

需要注意的是，综合国力这一概念是我国原创的政治概念，主要考虑了经济等软实力因素，是为了防止中国走苏联的老路，犯苏联发展经济时在军事上过度投资开支的错误。而相对的，国外关注的更多的是国家实力综合指数（Composite Index of National Capability，CINC）。该概念由J·大卫辛格在1963年为战争相关计划（Correlates of War）所创。它使用全世界百分比的平均在六个不同成分。这些成分代表人口统计学、经济学，和军事力量。但是国家实力综合指数只衡量硬实力并且可能没有表示出总体的国家实力。

由此可见，由我国创造的综合国力这一概念，在衡量与比较国家实力时，更加的全面和客观，褪去了旧时代的印记。

指标及数据来源

中国社科院综合国力指标

中国社科院建立了人均国民生产总值、社会结构、人口素质、生活质量四个部分的指标体系，可分解为以下16项指标：

  • 人均国民生产总值；
  • 农业产值在国民生产总值中的比重；
  • 第三产业在国民生产总值中的比重；
  • 出口总额在国民生产总值中的比重；
  • 城市人口占总人口的比重；
  • 非农业就业人口占就业人口的比重；
  • 教育经费占国民生产总值的比重（以上各项为社会结构）；
  • 中学生占12—17岁年龄人口的比重；
  • 大学生占20 —24岁年龄人口的比重；
  • 人口自然增长率；
  • 平均预期寿命；
  • 婴儿死亡率（8—12项为人口素质）；
  • 平均多少人有一个医生；
  • 平均每人每天摄取的热量；
  • 通货膨胀率；
  • 人均能源消耗量。

本文新增指标

  1. **本文尝试在现有指标的基础上添加以下指标**，以更全面的衡量一国的综合国力。

航天实力

  • 国家每年在航天领域的支出以及趋势（上升趋势为正相关，反之为负相关）
  • 在轨卫星数量
  • 航天从业人员总数
  • 发射成功数
  • 发动机技术
  • 专利数
  • 火箭运载能力
  • 商业化程度

军事力量

  • 军事支出占GDP比例
  • 军事人员总数
  • 军事人员在总人口中的比例
  • 装备水平, 军事装备指数（MEI）
  • 核力量
  • 战时动员能力（包括工业动员与人员动员）
  • 军事工业能力
  • 地缘环境

贫富差距

  • 最富有的5%的人的财富总值占所有人财富的比例，以及最贫穷的5%的人的财富总值占总量的比例。
  • 各年龄段之间的贫富差异。比如，35到45岁年龄的人的财富总值与25到35岁年龄的人的财富总值的比值。

医疗

  • 医疗支出占国民总支出的比例。
  • 医疗支出占60岁以上人群总支出的比例，这其中，医保报销比例和自费比例也作为考虑因素之一。
  • 购买医保的支出占国民支出的比例。

知识产权与科技发展

  • 年专利申请数量
  • 头部科技公司数量
  • 科学、技术、工程、数学等专业的年新增博士数量

互联网实力

  • 网民总数以及在总人口中的比例
  • 互联网产业占GDP比重

其他

  • 国民幸福指数（GNH）
  • 单亲家庭占比以及趋势（上升趋势为负相关，反之为正相关）
  • 本国媒体在海外的影响力
  • 移民数量，包括移入数量和移出数量；以及发展趋势。
  • 粮食储备

数据来源

经济类

民生类

军事类

其他

尝试给出数学模型

引入标度律

标度律（Scaling Law）描述了在相当大的间隔内彼此缩放的两个物理量之间的函数关系。标度律解释了诸如树木不能无限生长，公司与组织无法无限扩张的问题，即在两个物理量的关系中为其中之一提供了一个增长上界，本文认为这一思想可以应用在综合国力的计算中。

猜想

  1. 原有的模型，综合国力（CNP）与各个因素之间的关系都是正相关。**<font style="color:#F5222D;">但正如上文标度律引出的结论，本文认为很多变量无法无限增长（尤其在考虑多个相关变量时），即只能在某一区间内波动，如果超过这一区间，则会起到相反作用，对综合国力并无益处。</font>**
  3. 例一，军事人员总数这一指标对综合国力有正向贡献。但是如果结合军事人员数量在总人口中的占比这一指标综合考虑，如果占比过高，对一个国家的综合国力的贡献有可能是负的。
  5. 例二，拥有高等教育学历的人数（N）和国力之间显然是正相关关系，但当我们考虑进了高等教育质量（Q）这一因素时，我们就需要重新思考N的计算方式。当Q的值很高时，N越高显然说明了一国公民教育程度越高，CNP也越高。但当Q的值非常低时，N的值如果非常高，这就在一定程度上反映了某国高等教育的过度大众化和平庸化，在这种情况下，其对CNP的贡献有可能是负的。
  7. 此种算法的难点在于_**设置阈值**_。因为国情和发展阶段的不同，很难给出一个普适的阈值。
  9. <font style="color:#F5222D;">可以根据以往数据做机器学习预测，得出一个既适用于单独一个国家又能在各国横向比较中表现客观的阈值。</font>

简要算法

  1. 我们分为四大类：军事（M），民生（L），经济（E），科技（T）。
  3. 其中，军事包含上述军事力量和航天实力；民生包括社科院的社会机构和人口素质大类，以及上述的医疗和其他类别；经济包括人均国民生产总值和贫富差距；科技包括上述知识产权与科技发展和互联网实力。
  5. 此算法只考虑大类别在综合国力中的占比，如军事占比为30%，民生占比为20%，国民经济占比35%，科技占比15%。

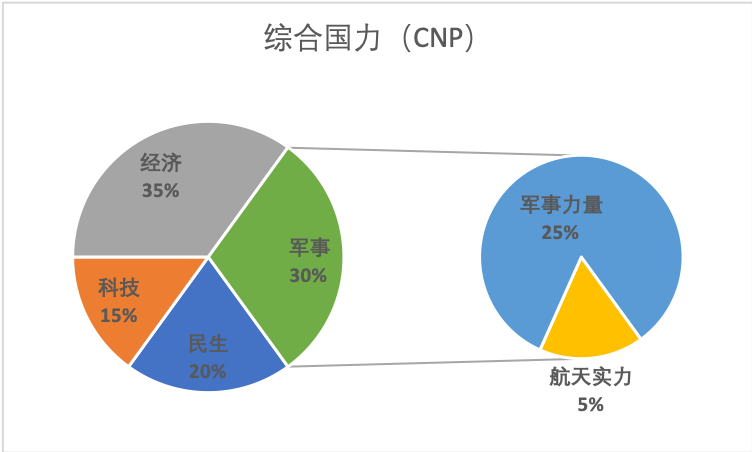
综合国力 - 图2

$ CNP = 0.3M + 0.2L + 0.15T + 0.35E $

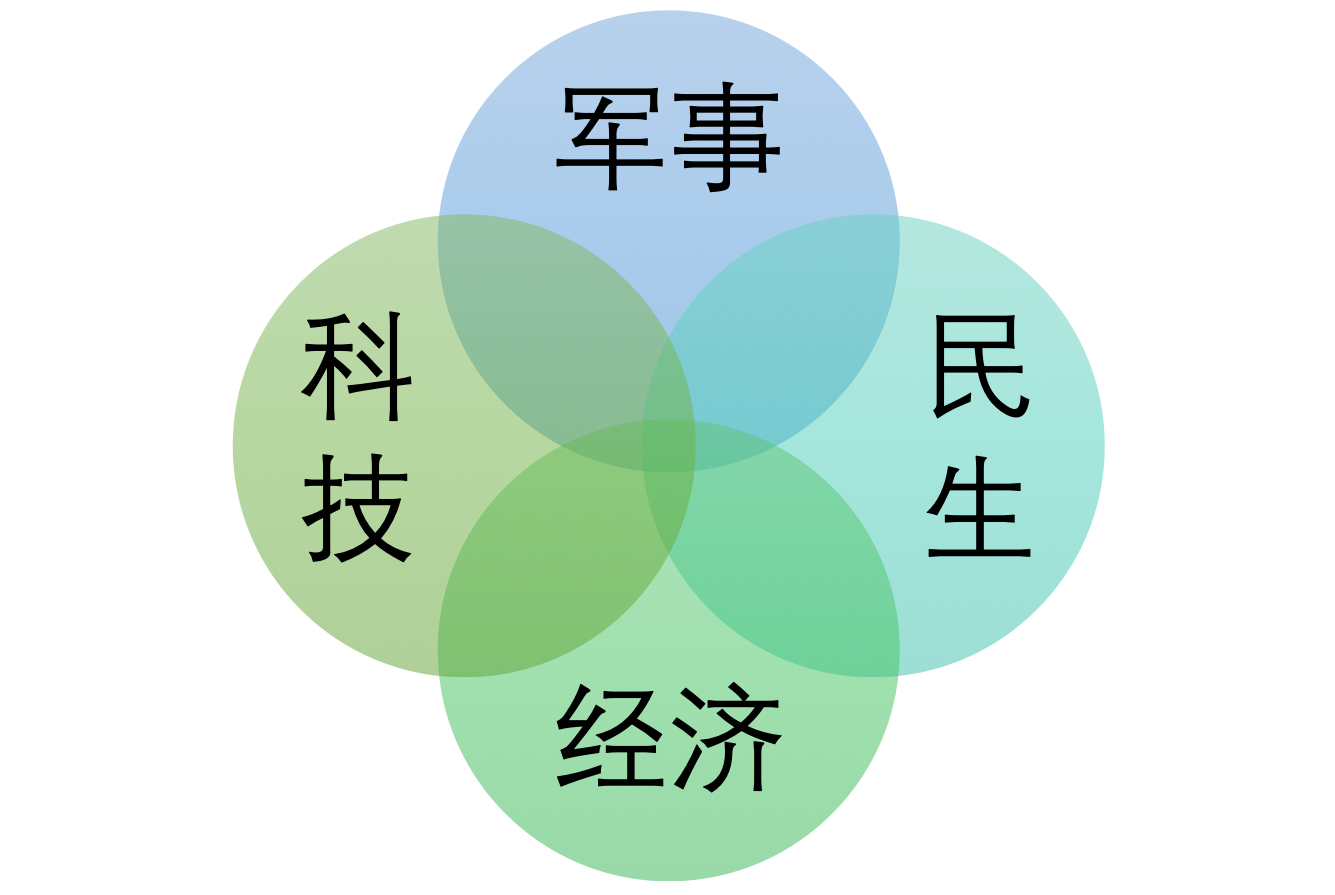
虽然我们给每一类一个固定的占比，但是有一点要明确，这四类并非独立，而是两两之间存在交集，互相影响，如下所示。

综合国力 - 图3

参考

[1] https://baike.so.com/doc/952786-1007190.html

[2] https://baike.baidu.com/item/克莱因公式/2825752

[3]https://baike.baidu.com/item/克莱因公式/2825752

[4] https://zh.wikipedia.org/zh-hans/综合国力

[5] https://www.un.org/zh/databases/

[6] https://en.wikipedia.org/wiki/Composite_Index_of_National_Capability