简介
生成流网络(GFlowNets)是一种在主动学习环境中对不同候选人进行抽样的方法,其训练目标是使他们按照给定的奖励函数近似抽样。
GFlowNets 灵感来源于信息在时序差分 RL 方法中的传播方式(Sutton 和 Barto,2018 年)。两者都依赖于 credit assignment 一致性原则,它们只有在训练收敛时才能实现渐近。由于状态空间中的路径数量呈指数级增长,因此实现梯度的精确计算比较困难,因此,这两种方法都依赖于不同组件之间的局部一致性和一个训练目标,即如果所有学习的组件相互之间都是局部一致性的,那么我们就得到了一个系统,该系统可以进行全局估计。
本文为主动学习场景提供了形式化理论基础和理论结果集的扩展,同时也为主动学习场景提供了更广泛的方式。GFlowNets 的特性使其非常适合从集合和图的分布中建模和采样,估计自由能和边缘分布,并用于从数据中学习能量函数作为马尔可夫链蒙特卡洛(Monte-Carlo Markov chains,MCMC)一个可学习的、可分摊(amortized)的替代方案。
GFlowNets 的关键特性是其学习了一个策略,该策略通过几个步骤对复合对象 s 进行采样,这样使得对对象 s 进行采样的概率 P_T (s) 与应用于该对象的给定奖励函数的值 R(s) 近似成正比。一个典型的例子是从正例数据集训练一个生成模型,GFlowNets 通过训练来匹配给定的能量函数,并将其转换为一个采样器,我们将其视为生成策略,因为复合对象 s 是通过一系列步骤构造的。这类似于 MCMC 方法的实现,不同的是,GFlowNets 不需要在此类对象空间中进行冗长的随机搜索,从而避免了 MCMC 方法难以处理模式混合的难题。GFlowNets 将这一难题转化为生成策略的分摊训练(amortized training)来处理。
本文的一个重要贡献是条件 GFlowNet 的概念,可用于计算不同类型(例如集合和图)联合分布上的自由能。这种边缘化还可以估计熵、条件熵和互信息。GFlowNets 还可以泛化,用来估计与丰富结果 (而不是一个纯量奖励函数) 相对应的多个流,这类似于分布式强化学习。
本文对原始 GFlowNet (Bengio 等人,2021 年)的理论进行了扩展,包括计算变量子集边缘概率的公式(或自由能公式),该公式现在可以用于更大集合的子集或子图 ;GFlowNet 在估计熵和互信息方面的应用;以及引入无监督形式的 GFlowNet(训练时不需要奖励函数,只需要观察结果)可以从帕累托边界进行采样。
基本的 GFlowNets 更类似于 bandits 算法(因为奖励仅在一系列动作的末尾提供),但 GFlowNets 可以通过扩展来考虑中间奖励,并根据回报进行采样。GFlowNet 的原始公式也仅限于离散和确定性环境,而本文建议如何解除这两种限制。最后,虽然 GFlowNets 的基本公式假设了给定的奖励或能量函数,但本文考虑了 GFlowNet 如何与能量函数进行联合学习,为新颖的基于能量的建模方法、能量函数和 GFlowNet 的模块化结构打开了大门。
基于流的生成模型
截至目前,生成模型主要以下4种::
- Component-by-Component(Auto-regressive model)
- AutoEncoder(VAE)
- Generative Adversarial Network(CycleGAN、cGAN、WGAN)
- Flow-based Generative Model(NICE、Real NVP、Glow)
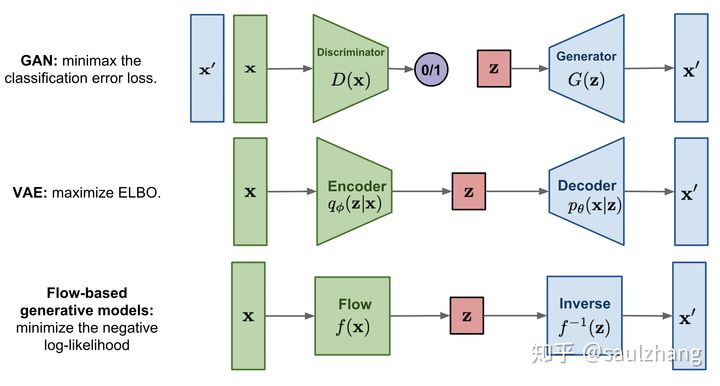
生成模型
所谓生成模型,就是给定训练数据,我们要生成与该数据分布相同的新样本。假设,训练数据服从分布 ,生成样本服从分布
,我们想要两个分布
和
相似。所以生成模型的本质,就是希望用一个我们知道的概率模型来拟合给定的训练样本,即我们能够写出一个带参数
的分布
。
神经网络作为万能的函数拟合器,却不能够随意拟合一个概率分布,因为概率分布有“非负”和“归一化”的要求。
对于图像生成,由于图像是由离散有限的像素点构成,我们可以通过离散分布进行描述(PixelRNN或者PixelCNN模型的思路),然而这种方法无法并行计算,计算特别慢。而且更多场景下,有很多连续性的数据,我们希望用连续的分布进行描述。
例如,我们可以使用高斯分布。我们可以写出各个分量独立的高斯分布作为一个新的连续性分布,但是这也只是很多连续分布中的极小一部分,是远远不够用的,因此,我们可以写成积分的形式,通过积分的形式构造出更多的分布:
其中, 是一般的标准高斯分布。
可以选择任意的高斯分布,理论上,这样的积分形式能够拟合任意分布。
有了这个分布,我们要求出参数 ,一般就是使用最大似然求解,我们需要最大化目标:
但是, 是积分的形式,一般来说很难计算。
比如GAN的目标就是通过生成器学习得到一个生成分布,并使其尽可能的接近于真实的数据分布。对于该过程我们可以表述为以下的公式:
目前生成器往往是参数量十分巨大的NN,所以的具体表达式我们很难获得,所以在GAN里面需要在生成分布和真实分布中进行采样,通过采样尽可能多的数据来近似两个不同的分布,然后引入判别器来衡量两个分布之间的差距,以此来引导NN的训练。
VAE和GAN从不同的方向避开了这个困难,VAE不直接优化上式,而是通过优化一个上界,得到近似的模型。GAN则通过生成器和判别器对抗的方式,绕开了这个困难。而在flow-based生成模型中,将会对上述的公式直接进行求解,这就是其与GAN,VAE存在的最大区别。
流模型
流模型有一个非常与众不同的特点是,它的转换通常是可逆的。也就是说,流模型不仅能找到从A分布变化到B分布的网络通路,并且该通路也能让B变化到A,简言之流模型找到的是一条A、B分布间的双工通路。当然,这样的可逆性是具有代价的——A、B的数据维度必须是一致的。
这里需要补充一点知识,已知两个概率密度函数
和
,这两个概率密度分布存在以下变换关系
,在两个不同的概率密度函数上对应的部分取
和
进行积分,根据两个函数对应部分积分的面积相等,可以得到关系式:
,其中
为函数
的雅可比矩阵,由于
,所以有
。
上面讲到的 其实就是下图中对应的采样分布,而
就对应生成分布。那么有了以上补充部分的结论便可得到
和
。
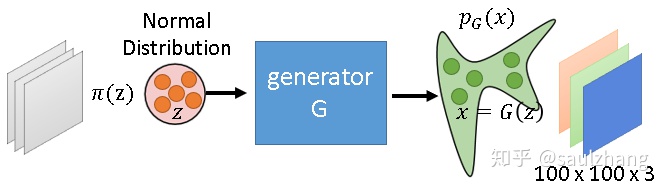
那么现在我们便可以把最上面的优化目标 转化为:
要求解以上的表达式就需要先计算出 和
,所以显而易见这里的生成器
必须是可逆的。在这里我们可以通过逆序来训练
,在真实分布中采样
,生成Normal Distribution中的sample
,maximize上面的objective function(这里一般需要保证
和
具有相同的尺寸)。
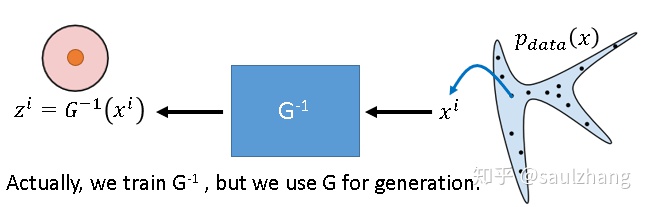
由于单个 受到了较多的约束,所以可能表征能力有限,需要注意的是这里的
是可以进行多层扩展的,其对应的关系式只要进行递推便可。

生成流网络
研究者的目标是使用估计量 Fˆ(s)和 Pˆ(s→s’|s)找到最能匹配需求的函数,如状态流函数 F(s)或转移概率函数 P(s→s’ |s),这些可能不符合 proper flow。因此,他们将这类学习机器称为 Generative Flow Networks(简称为 GFlowNets)。

个人理解,这个F相当于上图的G,通过一个流把初始样本分布转换成期望的分布。
需要注意的是,GFlowNet 的状态空间(state-space)可以轻松修改以适应底层状态空间,其中转换(transition)不会形成有向无环图(directed acyclic graph, DAG)。
对于从终端流(Terminal Flow)估计转换概率,在 Bengio et al. (2021)的设置中, 研究者得到了与「作为状态确定性函数的终端奖励函数 R 」相对应的终端流:

这样一来就可以扩展框架并以各种方式处理随机奖励。
GFlowNets 可以作为 MCMC Sampling 的替代方案。GFlowNet 方法分摊前期计算以训练生成器,为每个新样本产生非常有效的计算(构建单个配置,不需要链)。
流匹配和详细的平衡损失。为了训练 GFlowNet,研究者需要构建一个训练流程,该流程可以隐式地强制执行约束和偏好。他们将流匹配(flow-matching)或细致平衡条件(detailed balance condition)转换为可用的损失函数。
设有马尔科夫链
,状态空间为
,转移概率矩阵为
,以及我们关注的状态分布
,对于任意状态
,任意时刻
都满足:
,则称状态分布
满足马尔科夫链的细致平衡条件,该状态分布
就是马尔科夫链
的平稳分布。
对于奖励函数,研究者考虑了「奖励是随机而不是状态确定性函数」的设置。如果有一个像公式 44 中的奖励匹配损失,则终端流 F(s→s_f)的有效目标是预期奖励 E_R[R(s),因为这是给定 s 时最小化 R(s)上预期损失的值。
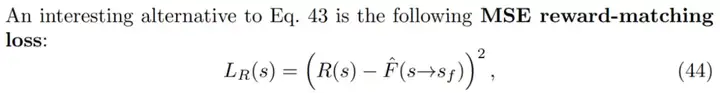
如果有一个像公式 43 中的奖励匹配损失,终端流 log F(s→s_f)的 log 有效目标是 log-reward E_R[log R(s)]的预期值。这表明了使用奖励匹配损失时,GFlowNets 可以泛化至匹配随机奖励。
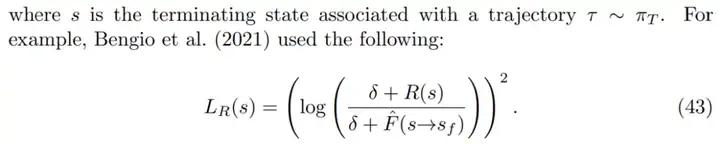
此外,GFlowNets 可以像离线强化学习一样离线训练。对于 GFlowNets 中的直接信用分配(Direct Credit Assignment),研究者认为可以将使用 GFlowNet 采样轨迹的过程等同于在随机循环神经网络中采样状态序列。让事情变得更复杂的原因有两个,其一这类神经网络不直接输出与某个目标匹配的预测,其二状态可能是离散(或者离散和连续共存)的。
这篇主要是给2106.04399.pdf (arxiv.org)这个论文补充了数学框架。

