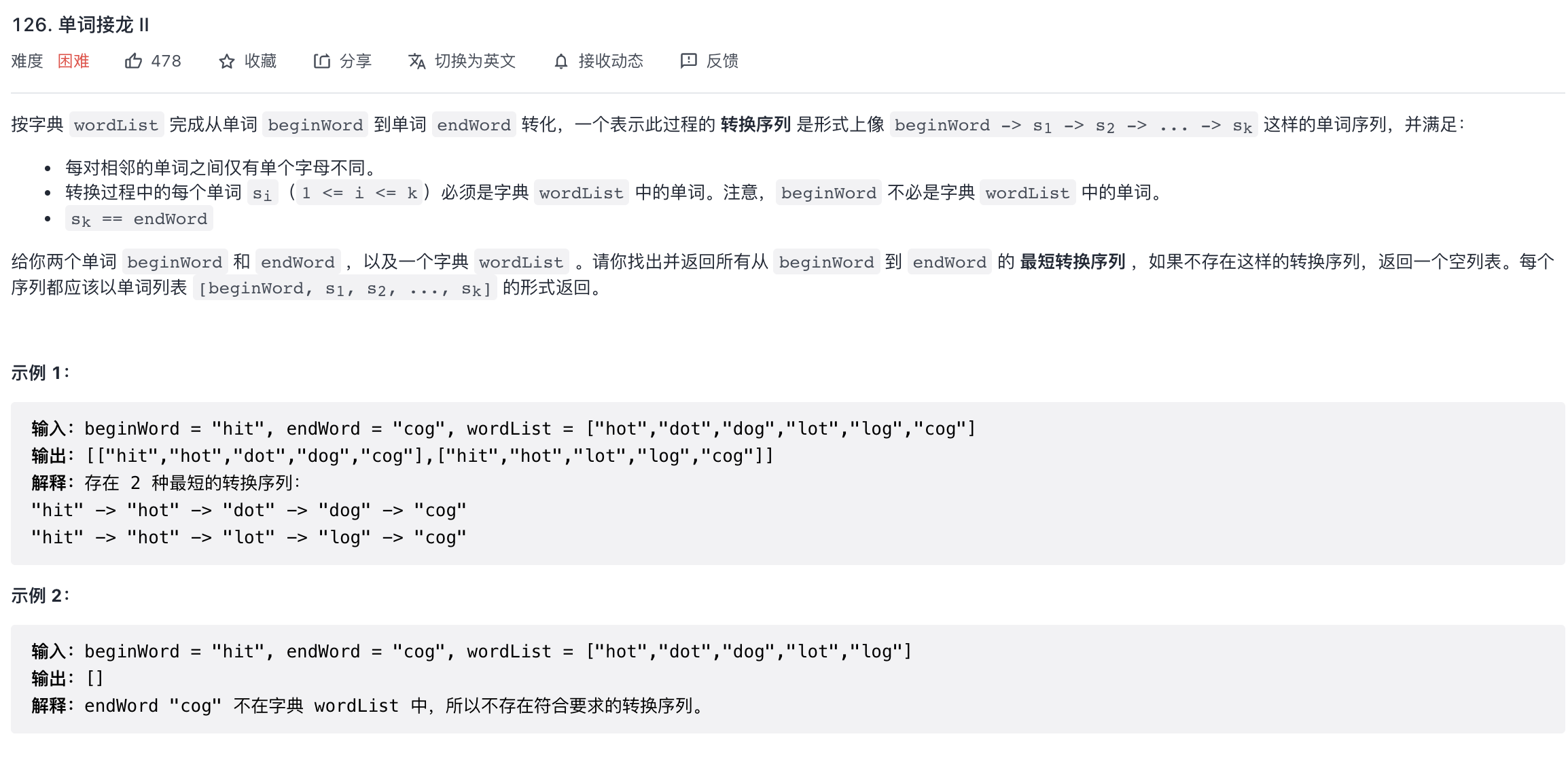
题目

类型：BFS
难度：困难

解题思路

题目中给出的单词和单词之间的关系构成了一张 无向图。因为根据转换的规则：两个单词有且只有一个字符不相等。如果可以从一个单词 word1 转换成为单词 word2，那么一定可以从单词 word2 转换成为 word1。

以例 1 为例，

beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

可以构建出这些单词之间的关系如下。

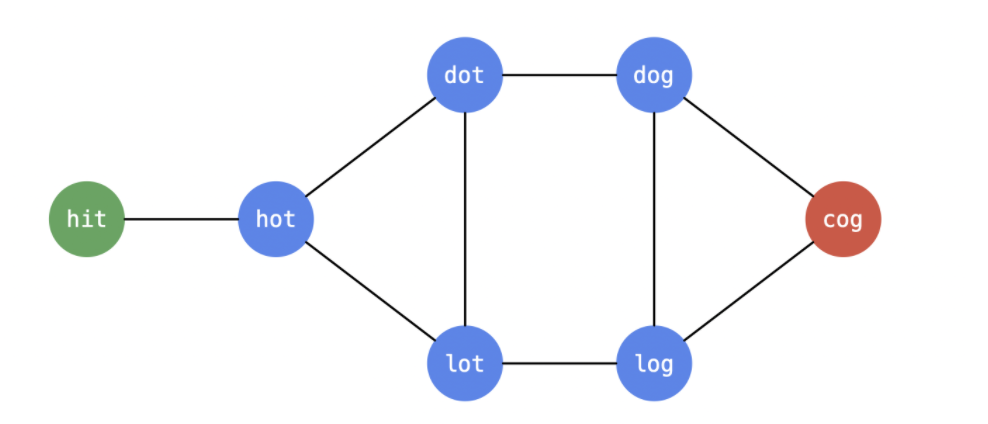
题目要我们找 最短转换序列，提示我们需要使用 广度优先遍历。广度优先遍历就是用于找无权图的最短路径。

要求返回 所有 从 beginWord 到 endWord 的最短转换序列，提示我们需要使用搜索算法（回溯算法、深度优先遍历）完成。

需要注意的
由于要找最短路径，连接 dot 与 lot 之间的边就不可以被记录下来，同理连接 dog 与 log 之间的边也不可以被记录。这是因为经过它们的边一定不会是最短路径。因此在广度优先遍历的时候，需要记录的图的关系如下图所示。

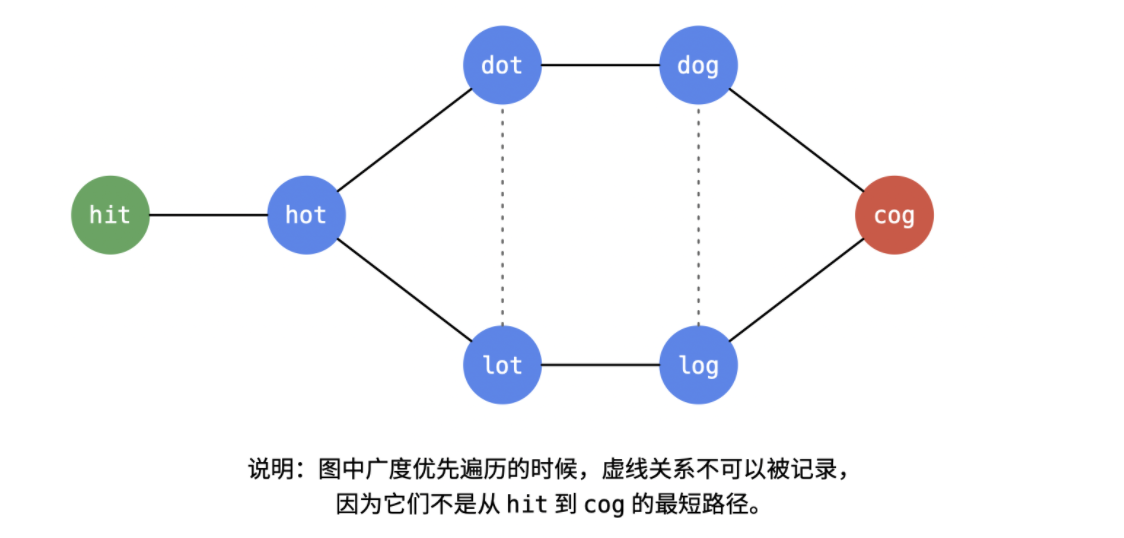
由于位于广度优先遍历同一层的单词如果它们之间有边连接，不可以被记录下来。因此需要一个哈希表记录遍历到的单词在第几层。理解下面这张图和图中的说明非常重要。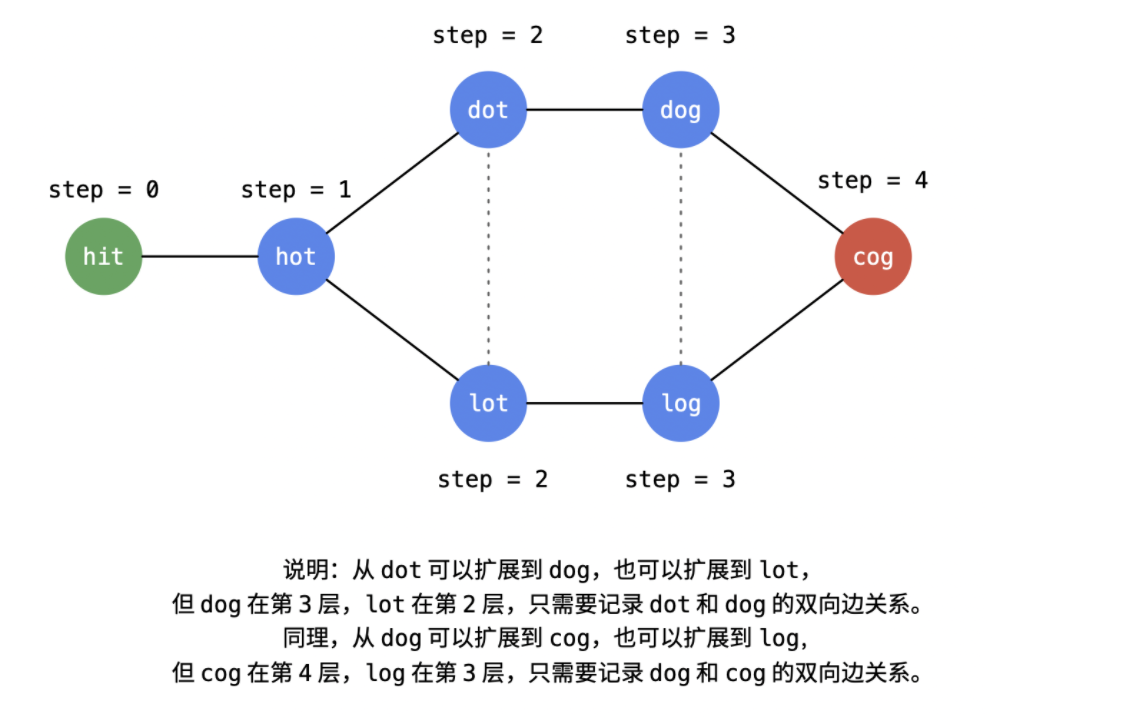

在广度优先遍历的时候，我们需要记录：从当前的单词 currWord 只变化了一个字符以后，且又在单词字典中的单词 nextWord 之间的单向关系（虽然实际上无向图，但是广度优先遍历是有方向的，我们解决这个问题可以只看成有向图），记为 from，它是一个映射关系：键是单词，值是广度优先遍历的时候从哪些单词可以遍历到「键」所表示的单词，使用哈希表来保存。

代码

class Solution {

    public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
        List<List<String>> res = new ArrayList<>();
        Set<String> dict = new HashSet<>(wordList);
        if (!dict.contains(endWord)) {
            return res;
        }
        dict.remove(beginWord);

        Map<String, Integer> steps = new HashMap<>();
        steps.put(beginWord, 0);
        Map<String, Set<String>> from = new HashMap<>();
        boolean found = bfs(beginWord, endWord, dict, steps, from);

        if (found) {
            Deque<String> path = new ArrayDeque<>();
            path.add(endWord);
            dfs(from, path, beginWord, endWord, res);
        }
        return res;
    }


    private boolean bfs(String beginWord, String endWord, Set<String> dict, Map<String, Integer> steps, Map<String, Set<String>> from) {
        int wordLen = beginWord.length();
        int step = 0;
        boolean found = false;

        Queue<String> queue = new LinkedList<>();
        queue.offer(beginWord);
        while (!queue.isEmpty()) {
            step++;
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                String currWord = queue.poll();
                char[] charArray = currWord.toCharArray();
                for (int j = 0; j < wordLen; j++) {
                    char origin = charArray[j];
                    for (char c = 'a'; c <= 'z'; c++) {
                        charArray[j] = c;
                        String nextWord = String.valueOf(charArray);
                        if (steps.containsKey(nextWord) && steps.get(nextWord) == step) {
                            from.get(nextWord).add(currWord);
                        }

                        if (!dict.contains(nextWord)) {
                            continue;
                        }
                        dict.remove(nextWord);
                        queue.offer(nextWord);
                        from.putIfAbsent(nextWord, new HashSet<>());
                        from.get(nextWord).add(currWord);
                        steps.put(nextWord, step);
                        if (nextWord.equals(endWord)) {
                            found = true;
                        }
                    }
                    charArray[j] = origin;
                }
            }
            if (found) {
                break;
            }
        }
        return found;
    }

    private void dfs(Map<String, Set<String>> from, Deque<String> path, String beginWord, String cur, List<List<String>> res) {
        if (cur.equals(beginWord)) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (String precursor : from.get(cur)) {
            path.addFirst(precursor);
            dfs(from, path, beginWord, precursor, res);
            path.removeFirst();
        }
    }
}